|
Parameter Space
The parameter space is the space of all possible parameter values that define a particular mathematical model. It is also sometimes called weight space, and is often a subset of finite-dimensional Euclidean space. In statistics, parameter spaces are particularly useful for describing parametric families of probability distributions. They also form the background for parameter estimation. In the case of extremum estimators for parametric models, a certain objective function is maximized or minimized over the parameter space. Theorems of existence and consistency of such estimators require some assumptions about the topology of the parameter space. For instance, compactness of the parameter space, together with continuity of the objective function, suffices for the existence of an extremum estimator. Sometimes, parameters are analyzed to view how they affect their statistical model. In that context, they can be viewed as inputs of a function, in which case the technical term for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space (mathematics)
In mathematics, a space is a set (sometimes known as a ''universe'') endowed with a structure defining the relationships among the elements of the set. A subspace is a subset of the parent space which retains the same structure. While modern mathematics uses many types of spaces, such as Euclidean spaces, linear spaces, topological spaces, Hilbert spaces, or probability spaces, it does not define the notion of "space" itself. A space consists of selected mathematical objects that are treated as points, and selected relationships between these points. The nature of the points can vary widely: for example, the points can represent numbers, functions on another space, or subspaces of another space. It is the relationships that define the nature of the space. More precisely, isomorphic spaces are considered identical, where an isomorphism between two spaces is a one-to-one correspondence between their points that preserves the relationships. For example, the relationships b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Domain Of A Function
In mathematics, the domain of a function is the Set (mathematics), set of inputs accepted by the Function (mathematics), function. It is sometimes denoted by \operatorname(f) or \operatornamef, where is the function. In layman's terms, the domain of a function can generally be thought of as "what x can be". More precisely, given a function f\colon X\to Y, the domain of is . In modern mathematical language, the domain is part of the definition of a function rather than a property of it. In the special case that and are both sets of real numbers, the function can be graphed in the Cartesian coordinate system. In this case, the domain is represented on the -axis of the graph, as the projection of the graph of the function onto the -axis. For a function f\colon X\to Y, the set is called the ''codomain'': the set to which all outputs must belong. The set of specific outputs the function assigns to elements of is called its ''Range of a function, range'' or ''Image (mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Set
In mathematical analysis and related areas of mathematics, a set is called bounded if all of its points are within a certain distance of each other. Conversely, a set which is not bounded is called unbounded. The word "bounded" makes no sense in a general topological space without a corresponding metric. '' Boundary'' is a distinct concept; for example, a circle (not to be confused with a disk) in isolation is a boundaryless bounded set, while the half plane is unbounded yet has a boundary. A bounded set is not necessarily a closed set and vice versa. For example, a subset of a 2-dimensional real space constrained by two parabolic curves and defined in a Cartesian coordinate system is closed by the curves but not bounded (so unbounded). Definition in the real numbers A set of real numbers is called ''bounded from above'' if there exists some real number (not necessarily in ) such that for all in . The number is called an upper bound of . The terms ''bounded from b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mandelbrot Set
The Mandelbrot set () is a two-dimensional set (mathematics), set that is defined in the complex plane as the complex numbers c for which the function f_c(z)=z^2+c does not Stability theory, diverge to infinity when Iteration, iterated starting at z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value. This set was first defined and drawn by Robert W. Brooks and Peter Matelski in 1978, as part of a study of Kleinian groups. Afterwards, in 1980, Benoit Mandelbrot obtained high-quality visualizations of the set while working at IBM's Thomas J. Watson Research Center in Yorktown Heights, New York. Images of the Mandelbrot set exhibit an infinitely complicated Boundary (topology), boundary that reveals progressively ever-finer Recursion, recursive detail at increasing magnifications; mathematically, the boundary of the Mandelbrot set is a ''fractal curve''. The "style" of this recursive detail depends on the region of the set boundary being ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows for a geometric interpretation of complex numbers. Under addition, they add like vector (geometry), vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates: the magnitude or ' of the product is the product of the two absolute values, or moduli, and the angle or ' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes called the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol , which can be sepa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Dynamics
Complex dynamics, or holomorphic dynamics, is the study of dynamical systems obtained by Iterated function, iterating a complex analytic mapping. This article focuses on the case of algebraic dynamics, where a polynomial or rational function is iterated. In geometric terms, that amounts to iterating a mapping from some algebraic variety to itself. The related theory of arithmetic dynamics studies iteration over the rational numbers or the p-adic numbers instead of the complex numbers. Dynamics in complex dimension 1 A simple example that shows some of the main issues in complex dynamics is the mapping f(z)=z^2 from the complex numbers C to itself. It is helpful to view this as a map from the complex projective line \mathbf^1 to itself, by adding a point \infty to the complex numbers. (\mathbf^1 has the advantage of being compact space, compact.) The basic question is: given a point z in \mathbf^1, how does its ''orbit'' (or ''forward orbit'') :z,\; f(z)=z^2,\; f(f(z))=z^4, f(f(f(z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
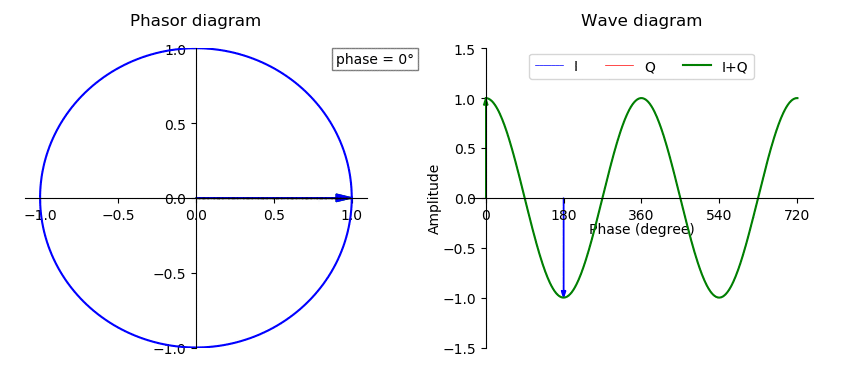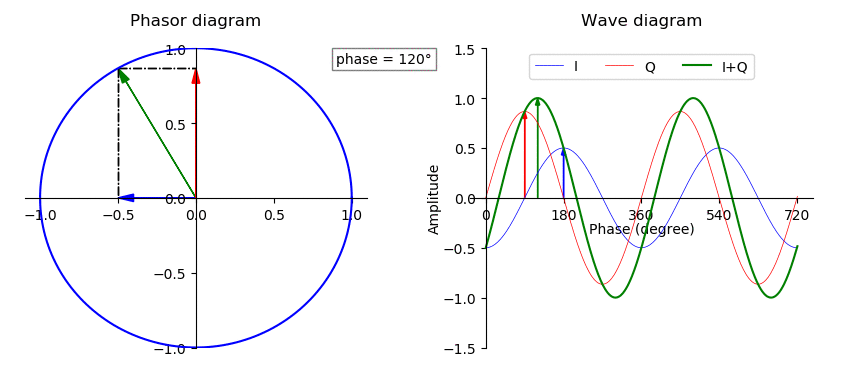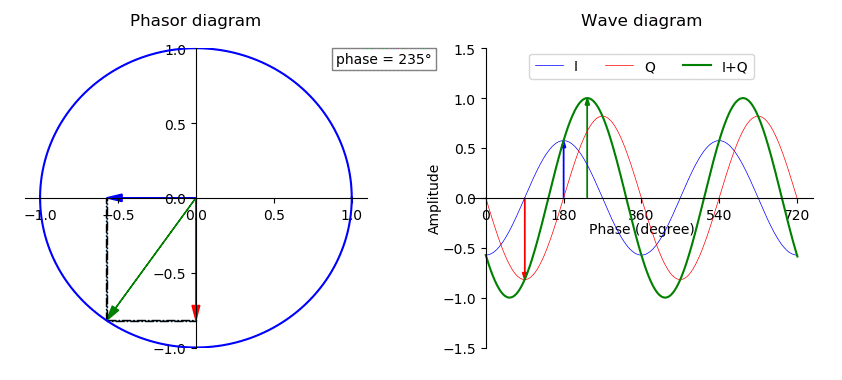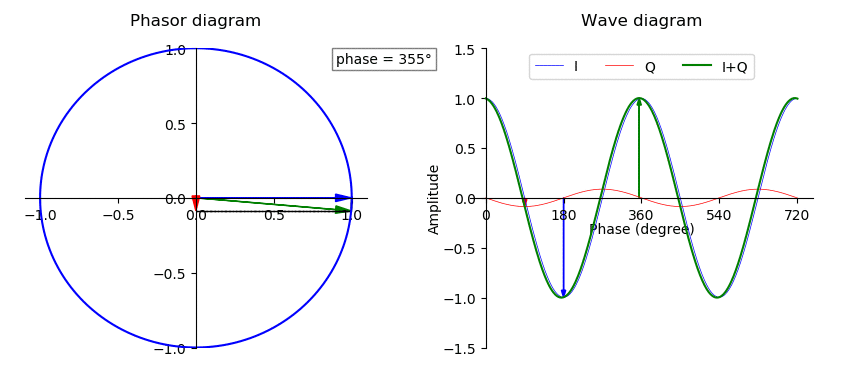
Phase (waves)
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or angular speed) is the magnitude of the pseudovector quantity '' angular velocity''. (UP1) Angular frequency can be obtained multiplying '' rotational frequency'', ''ν'' (or ordinary ''frequency'', ''f'') by a full turn (2 radians): . It can also be formulated as , the instantaneous rate of change of the angular displacement, ''θ'', with respect to time, ''t''. (11 pages) Unit In SI[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplitude (see below), which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a periodic function is sometimes called the amplitude. Definitions Peak amplitude and semi-amplitude For symmetric periodic waves, like sine waves or triangle waves, ''peak amplitude'' and ''semi amplitude'' are the same. Peak amplitude In audio system measurements, telecommunications and others where the measurand is a signal that swings above and below a reference value but is not sinusoidal, peak amplitude is often used. If the reference is zero, this is the maximum absolute value of the signal; if the reference is a mean value ( DC component), the peak amplitude is the maximum ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic function, periodic wave whose waveform (shape) is the trigonometric function, trigonometric sine, sine function. In mechanics, as a linear motion over time, this is ''simple harmonic motion''; as rotation, it corresponds to ''uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase (waves), phase) are linear combination, linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically ( fixed points, periodic orbits, or chaotic attractors) of a system as a function of a bifurcation parameter in the system. It is usual to represent stable values with a solid line and unstable values with a dotted line, although often the unstable points are omitted. Bifurcation diagrams enable the visualization of bifurcation theory. In the context of discrete-time dynamical systems, the diagram is also called orbit diagram. Logistic map An example is the bifurcation diagram of the logistic map: x_=rx_n(1-x_n). The bifurcation parameter ''r'' is shown on the horizontal axis of the plot and the vertical axis shows the set of values of the logistic function visited asymptotically from almost all initial conditions. The bifurcation diagram shows the forking of the periods of stable orbits from 1 to 2 to 4 to 8 etc. Each of these bifurcation poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Real Numbers
In mathematics, the set of positive real numbers, \R_ = \left\, is the subset of those real numbers that are greater than zero. The non-negative real numbers, \R_ = \left\, also include zero. Although the symbols \R_ and \R^ are ambiguously used for either of these, the notation \R_ or \R^ for \left\ and \R_^ or \R^_ for \left\ has also been widely employed, is aligned with the practice in algebra of denoting the exclusion of the zero element with a star, and should be understandable to most practicing mathematicians. In a complex plane, \R_ is identified with the positive real axis, and is usually drawn as a horizontal ray. This ray is used as reference in the polar form of a complex number. The real positive axis corresponds to complex numbers z = , z, \mathrm^, with argument \varphi = 0. Properties The set \R_ is closed under addition, multiplication, and division. It inherits a topology from the real line and, thus, has the structure of a multiplicative topological group or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |