|
Negative Binomial Distribution
In probability theory and statistics, the negative binomial distribution, also called a Pascal distribution, is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified/constant/fixed number of successes r occur. For example, we can define rolling a 6 on some dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success (r=3). In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution. An alternative formulation is to model the number of total trials (instead of the number of failures). In fact, for a specified (non-random) number of successes , the number of failures is random because the number of total trials is random. For example, we could use the negative binomial distribution to model the number of days (random) a certain machin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Distribution
In probability theory and statistics, the binomial distribution with parameters and is the discrete probability distribution of the number of successes in a sequence of statistical independence, independent experiment (probability theory), experiments, each asking a yes–no question, and each with its own Boolean-valued function, Boolean-valued outcome (probability), outcome: ''success'' (with probability ) or ''failure'' (with probability ). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., , the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the binomial test of statistical significance. The binomial distribution is frequently used to model the number of successes in a sample of size drawn with replacement from a population of size . If the sampling is carried out without replacement, the draws ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
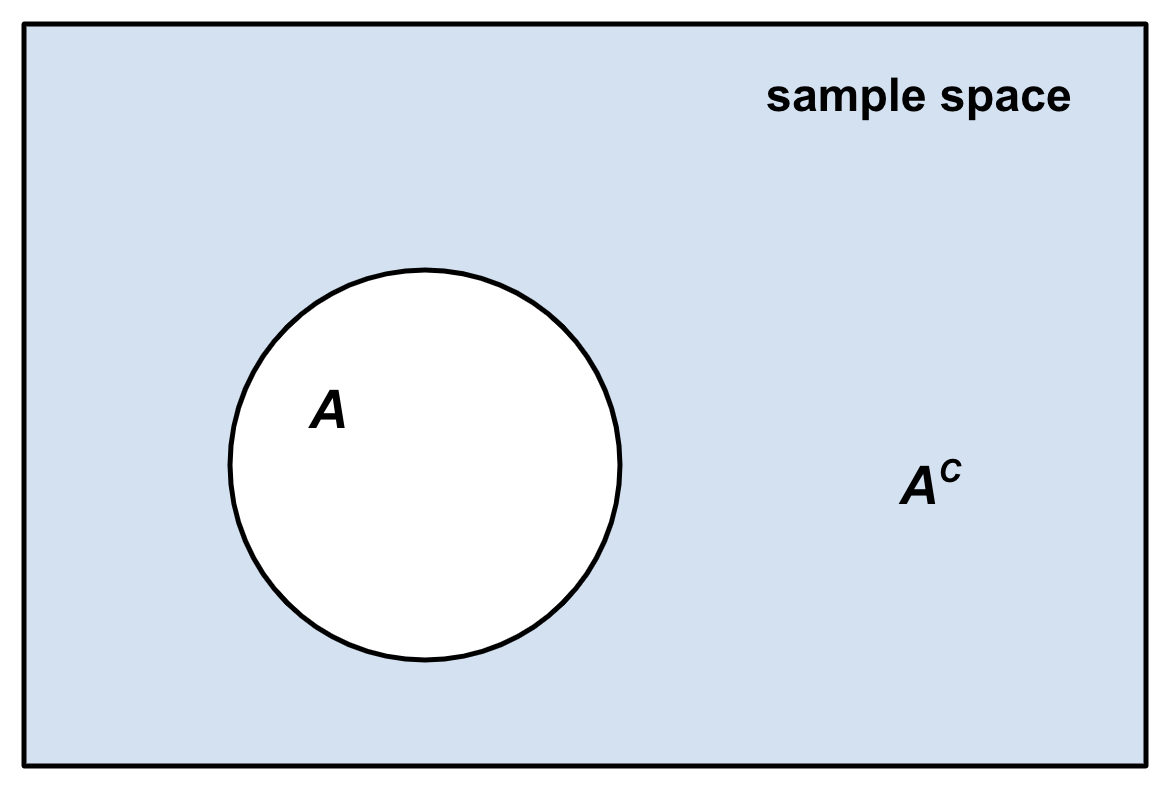
Complementary Event
In probability theory, the complement of any event ''A'' is the event ot ''A'' i.e. the event that ''A'' does not occur.Robert R. Johnson, Patricia J. Kuby: ''Elementary Statistics''. Cengage Learning 2007, , p. 229 () The event ''A'' and its complement ot ''A''are mutually exclusive and exhaustive. Generally, there is only one event ''B'' such that ''A'' and ''B'' are both mutually exclusive and exhaustive; that event is the complement of ''A''. The complement of an event ''A'' is usually denoted as ''A′'', ''Ac'', \neg''A'' or '. Given an event, the event and its complementary event define a Bernoulli trial: did the event occur or not? For example, if a typical coin is tossed and one assumes that it cannot land on its edge, then it can either land showing "heads" or "tails." Because these two outcomes are mutually exclusive (i.e. the coin cannot simultaneously show both heads and tails) and collectively exhaustive (i.e. there are no other possible outcom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Binomial Regression
Negative may refer to: Science and mathematics * Negative number * Minus sign (−), the mathematical symbol * Negative mass * Negative energy * Negative charge, one of the two types of electric charge * Negative (electrical polarity), in electric circuits * Negative result (other) * Negative lens, in optics Photography * Negative (photography), an image with inverted luminance or a strip of film with such an image * Original camera negative, the film in a motion picture camera which captures the original image * Paper negative, a negative image printed on paper used to create the final print of a photograph Linguistics * A negative answer, commonly expressed with the word No (word), ''no'' * A type of grammatical construction; see affirmative and negative *A double negative is a construction occurring when two forms of grammatical negation are used in the same sentence. Music * Negative (Finnish band), a Finnish band established in 1997 * Negative (Serbian ba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Length Of Stay
Length of stay (LOS) is the duration of a single episode of hospitalization. patient, Inpatient days are calculated by subtracting day of admission from day of :wikt:discharge, discharge. Analysis A common statistic associated with length of stay is the average length of stay (ALOS), a mean calculated by dividing the sum of inpatient days by the number of patients admissions with the same diagnosis-related group classification. A variation in the calculation of ALOS can be to consider only length of stay during the period under analysis. Length of stay is typically highly skewness, skewed and so statistical approaches taking that into account are recommended. While the mean length of stay is useful from the point of view of costs, it may be a poor statistic in terms of representing a typical length of stay, and the median may be preferred. It is useful to be able to predict an individual's expected length of stay or to model length of stay to determine factors that affect it. Vari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odds
In probability theory, odds provide a measure of the probability of a particular outcome. Odds are commonly used in gambling and statistics. For example for an event that is 40% probable, one could say that the odds are or When gambling, odds are often given as the ratio of the possible net profit ''to'' the possible net loss. However in many situations, you pay the possible loss ("stake" or "wager") up front and, if you win, you are paid the net win plus you also get your stake returned. So wagering 2 at , pays out , which is called When Moneyline odds are quoted as a positive number , it means that a wager pays When Moneyline odds are quoted as a negative number , it means that a wager pays Odds have a simple relationship with probability. When probability is expressed as a number between 0 and 1, the relationships between probability and odds are as follows. Note that if probability is to be expressed as a percentage these probability values should be multiplied ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clustering Coefficient
In graph theory, a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties; this likelihood tends to be greater than the average probability of a tie randomly established between two nodes (Holland and Leinhardt, 1971; Watts and Strogatz, 1998). Two versions of this measure exist: the global and the local. The global version was designed to give an overall indication of Clustering_coefficient#Global_clustering_coefficient, the clustering in the network, whereas the local gives an indication of the Clustering_coefficient#Local_clustering_coefficient, extent of "clustering" of a single node. Local clustering coefficient The local clustering coefficient of a vertex (graph theory), vertex (node) in a Graph (discrete mathematics), graph quantifies how close its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape Parameter
In probability theory and statistics, a shape parameter (also known as form parameter) is a kind of numerical parameter of a parametric family of probability distributionsEveritt B.S. (2002) Cambridge Dictionary of Statistics. 2nd Edition. CUP. that is neither a location parameter nor a scale parameter (nor a function of these, such as a rate parameter). Such a parameter must affect the ''shape (geometry), shape'' of a distribution rather than simply shifting it (as a location parameter does) or stretching/shrinking it (as a scale parameter does). For example, "peakedness" refers to how round the main peak is. Estimation Many estimators measure location or scale; however, estimators for shape parameters also exist. Most simply, they can be estimated in terms of the higher moment (mathematics), moments, using the Method of moments (statistics), method of moments, as in the ''skewness'' (3rd moment) or ''kurtosis'' (4th moment), if the higher moments are defined and finite. Estimato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extension To Real-valued R
Extension, extend or extended may refer to: Mathematics Logic or set theory * Axiom of extensionality * Extensible cardinal * Extension (model theory) * Extension (proof theory) * Extension (predicate logic), the set of tuples of values that satisfy the predicate * Extension (semantics), the set of things to which a property applies * Extension (simplicial set) * Extension by definitions * Extensional definition, a definition that enumerates every individual a term applies to * Extensionality Other uses * Extension of a function, defined on a larger domain * Extension of a polyhedron, in geometry * Extension of a line segment (finite) into an infinite line (e.g., extended base) * Exterior algebra, Grassmann's theory of extension, in geometry * Field extension, in Galois theory * Group extension, in abstract algebra and homological algebra * Homotopy extension property, in topology * Kolmogorov extension theorem, in probability theory * Linear extension, in order theory * S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Linear Model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by allowing the magnitude of the variance of each measurement to be a function of its predicted value. Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed. Intuition Ordinary linear regression predicts the expected value of a given unknown quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A model with exactly one explanatory variable is a ''simple linear regression''; a model with two or more explanatory variables is a multiple linear regression. This term is distinct from multivariate linear regression, which predicts multiple correlated dependent variables rather than a single dependent variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimation theory, estimated from the data. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |