|
Myriagon
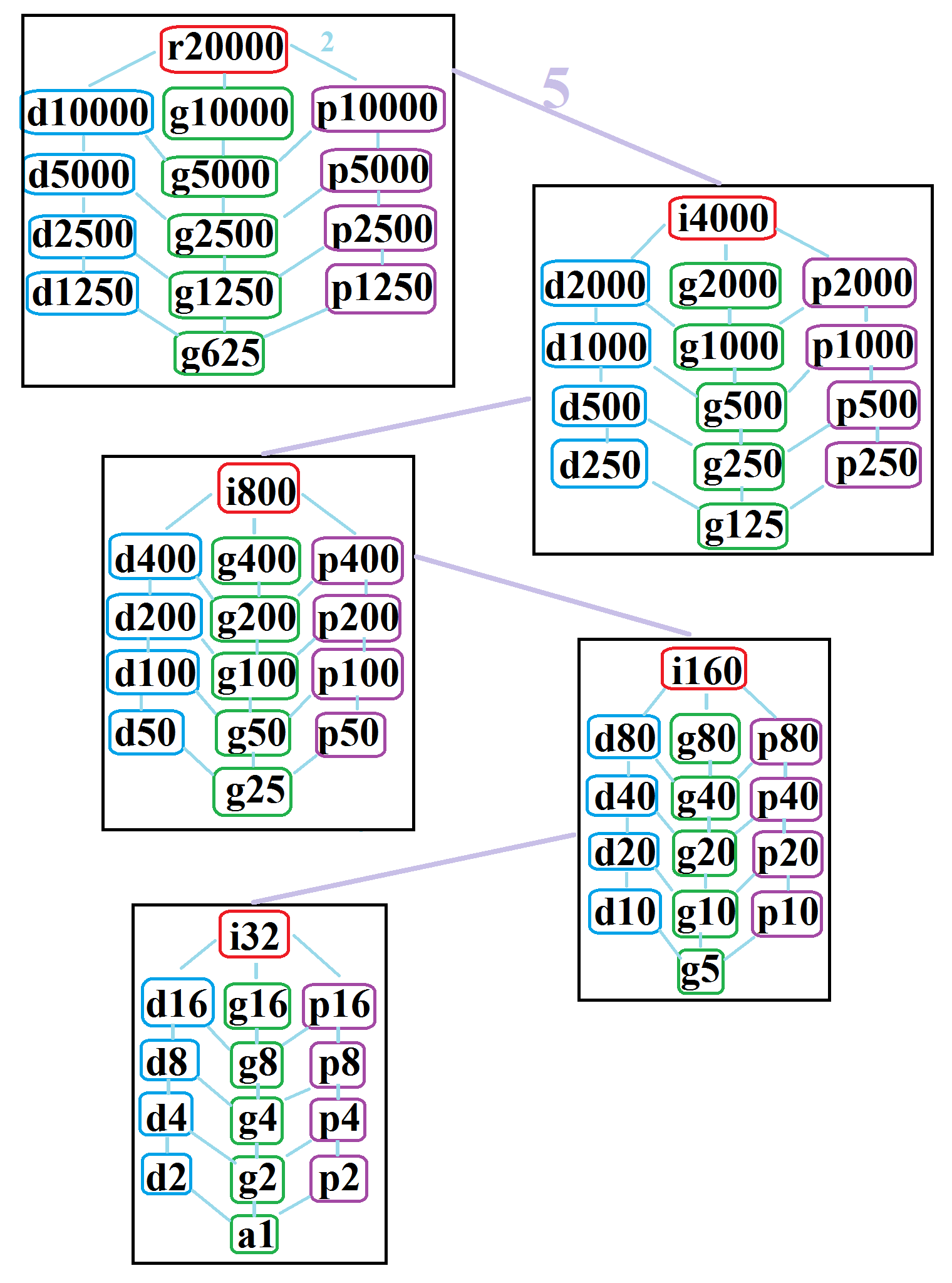
In geometry, a myriagon or 10000-gon is a polygon with 10000 sides. Several philosophers have used the regular myriagon to illustrate issues regarding thought. Meditation VI by Descartes (English translation). Regular myriagon A regular myriagon is represented by Schläfli symbol and can be constructed as a truncated 5000-gon, t, or a twice-truncated 2500-gon, tt, or a thrice-truncated 1250-gon, ttt, or a four-fold-truncated 625-gon, tttt. The measure of each internal angle in a regular myriagon is 179.964°. The area of a regular myriagon with sides of length ''a'' is given by :A = 2500a^2 \cot \frac The result differs from the area of its circumscribed circle by up to 400 parts per billion. Because 10,000 = 24 × 54, the number of sides is neither a product of distinct Fermat primes nor a power of two. Thus the regular myriagon is not a constructible polygon. Indeed, it is not even constructible with the use of an angle trisector, as the number of sides is neither a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chiliagon
In geometry, a chiliagon () or 1,000-gon is a polygon with 1,000 sides. Philosophers commonly refer to chiliagons to illustrate ideas about the nature and workings of thought, meaning, and mental representation. Regular chiliagon A '' regular chiliagon'' is represented by Schläfli symbol and can be constructed as a truncated 500-gon, t, or a twice-truncated 250-gon, tt, or a thrice-truncated 125-gon, ttt. The measure of each internal angle in a regular chiliagon is 179°38'24" or \fracrad. The area of a regular chiliagon with sides of length ''a'' is given by :A = 250a^2 \cot \frac \simeq 79577.2\,a^2 This result differs from the area of its circumscribed circle by less than 4 parts per million. Because 1,000 = 23 × 53, the number of sides is neither a product of distinct Fermat primes nor a power of two. Thus the regular chiliagon is not a constructible polygon. Indeed, it is not even constructible with the use of an angle trisector, as the number of sides is neith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex polygon, convex'' or ''star polygon, star''. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties These properties apply to all regular polygons, whether convex or star polygon, star: *A regular ''n''-sided polygon has rotational symmetry of order ''n''. *All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. *Together with the property of equal-length sides, this implies that every regular polygon also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain. The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' or ''corners''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a ''solid polygon''. The interior of a solid polygon is its ''body'', also known as a ''polygonal region'' or ''polygonal area''. In contexts where one is concerned only with simple and solid polygons, a ''polygon'' may refer only to a simple polygon or to a solid polygon. A polygonal chain may cross over itself, creating star polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flatland
''Flatland: A Romance of Many Dimensions'' is a satirical novella by the English schoolmaster Edwin Abbott Abbott, first published in 1884 by Seeley & Co. of London. Written pseudonymously by "A Square", the book used the fictional two-dimensional world of Flatland to comment on the hierarchy of Victorian culture, but the novella's more enduring contribution is its examination of dimensions. A sequel, '' Sphereland'', was written by Dionys Burger in 1957. Several films have been based on ''Flatland'', including the feature film '' Flatland'' (2007). Other efforts have been short or experimental films, including one narrated by Dudley Moore and the short films '' Flatland: The Movie'' (2007) and '' Flatland 2: Sphereland'' (2012). Plot The story describes a two-dimensional world inhabited by geometric figures (flatlanders); women are line segments, while men are polygons with various numbers of sides. The narrator is a square, a member of the caste of gentlemen and p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Figure
In geometry, a generalized polygon can be called a polygram, and named specifically by its number of sides. All polygons are polygrams, but they can also include disconnected sets of edges, called a compound polygon. For example, a regular pentagram, , has 5 sides, and the regular hexagram, or 2, has 6 sides divided into two triangles. A regular polygram can either be in a set of regular star polygons (for gcd(''p'',''q'') = 1, ''q'' > 1) or in a set of regular polygon compounds (if gcd(''p'',''q'') > 1). Etymology The polygram names combine a numeral prefix, such as ''penta-'', with the Greek suffix '' -gram'' (in this case generating the word ''pentagram''). The prefix is normally a Greek cardinal, but synonyms using other prefixes exist. The ''-gram'' suffix derives from ''γραμμῆς'' (''grammos'') meaning a line. Generalized regular polygons A regular polygram, as a general regular polygon, is denoted by its Schläfli symbol , where ''p'' and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coprime
In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equivalent to their greatest common divisor (GCD) being 1. One says also ''is prime to'' or ''is coprime with'' . The numbers 8 and 9 are coprime, despite the fact that neither—considered individually—is a prime number, since 1 is their only common divisor. On the other hand, 6 and 9 are not coprime, because they are both divisible by 3. The numerator and denominator of a reduced fraction are coprime, by definition. Notation and testing When the integers and are coprime, the standard way of expressing this fact in mathematical notation is to indicate that their greatest common divisor is one, by the formula or . In their 1989 textbook '' Concrete Mathematics'', Ronald Graham, Donald Knuth, and Oren Patashnik proposed an alte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, Decagram (geometry)#Related figures, certain notable ones can arise through truncation operations on regular simple or star polygons. Branko Grünbaum identified two primary usages of this terminology by Johannes Kepler, one corresponding to the regular star polygons with List of self-intersecting polygons, intersecting edges that do not generate new vertices, and the other one to the isotoxal Concave polygon, concave simple polygons.Grünbaum & Shephard (1987). Tilings and Patterns. Section 2.5 Polygram (geometry), Polygrams include polygons like the pentagram, but also compound figures like the hexagram. One definition of a ''star polygon'', used in turtle graphics, is a polygon having ''q'' ≥ 2 Turn (geometry), turns (''q'' is called the turning number or Density (polygon), density), like in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Horton Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician. He was active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches of recreational mathematics, most notably the invention of the cellular automaton called the Game of Life. Born and raised in Liverpool, Conway spent the first half of his career at the University of Cambridge before moving to the United States, where he held the John von Neumann Professorship at Princeton University for the rest of his career. On 11 April 2020, at age 82, he died of complications from COVID-19. Early life and education Conway was born on 26 December 1937 in Liverpool, the son of Cyril Horton Conway and Agnes Boyce. He became interested in mathematics at a very early age. By the time he was 11, his ambition was to become a mathematician. After leaving sixth form, he studied mathematics at Gonville and Caius Coll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, generated by a single element. That is, it is a set (mathematics), set of Inverse element, invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as an integer Exponentiation, power of g in multiplicative notation, or as an integer multiple of g in additive notation. This element g is called a ''Generating set of a group, generator'' of the group. Every infinite cyclic group is isomorphic to the additive group \Z, the integers. Every finite cyclic group of Order (group theory), order n is isomorphic to the additive group of Quotient group, Z/''n''Z, the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Symmetry
In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. In geometry, or refers to the symmetries of the -gon, a group of order . In abstract algebra, refers to this same dihedral group. This article uses the geometric convention, . Definition The word "dihedral" comes from "di-" and "-hedron". The latter comes from the Greek word hédra, which means "face of a geometrical solid". Overall it thus refers to the two faces of a polygon. Elements A regular polygon with n sides has 2n different symmetries: n rotational symmetries and n reflection symmetries. Usually, we take n \ge 3 here. The associated rotations and reflections make up the dihedral group \mathrm_n. If n is odd, each axis o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |