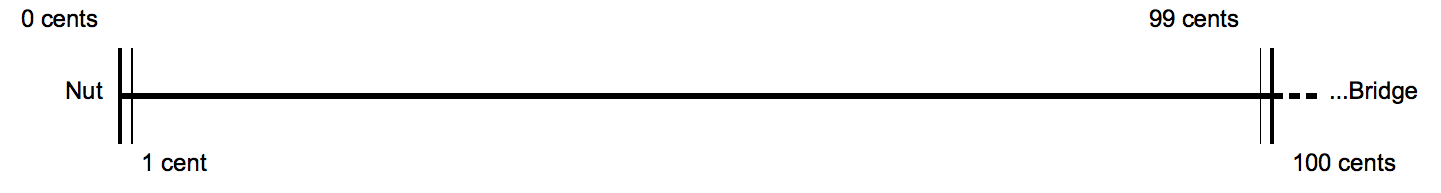|
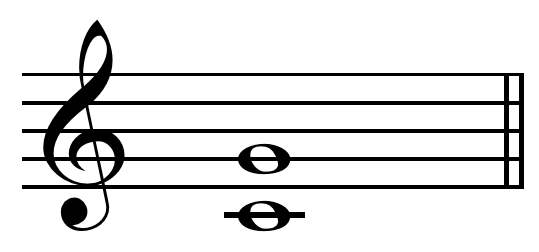
Major Third
In music theory, a third is a Interval (music), musical interval encompassing three staff positions (see Interval (music)#Number, Interval number for more details), and the major third () is a third spanning four Semitone, half steps or two Whole step, whole steps. Along with the minor third, the major third is one of two commonly occurring thirds. It is described as ''major'' because it is the larger interval of the two: The major third spans four semitones, whereas the minor third only spans three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished third, Diminished and augmented thirds are shown on the musical staff the same number of lines and spaces apart, but contain a different number of semitones in pitch (two and five). Harmonic and non-harmonic thirds The major third may be derived from the harmonic series (music), harmonic series as the interval be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Sixth
In music theory, a minor sixth is a musical interval encompassing six staff positions (see Interval number for more details), and is one of two commonly occurring sixths (the other one being the major sixth). It is qualified as ''minor'' because it is the smaller of the two: the minor sixth spans eight semitones, the major sixth nine. For example, the interval from A to F is a minor sixth, as the note F lies eight semitones above A, and there are six staff positions from A to F. Diminished and augmented sixths span the same number of staff positions, but consist of a different number of semitones (seven and ten respectively). Equal temperament In 12-tone equal temperament (12-ET), the minor sixth is enharmonically equivalent to the augmented fifth. It occurs in first inversion major and dominant seventh chords and second inversion minor chords. It is equal to eight semitones, i.e. a ratio of 28/12:1 or simplified to 22/3:1 (about 1.587), or 800 cents. Just temperament ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
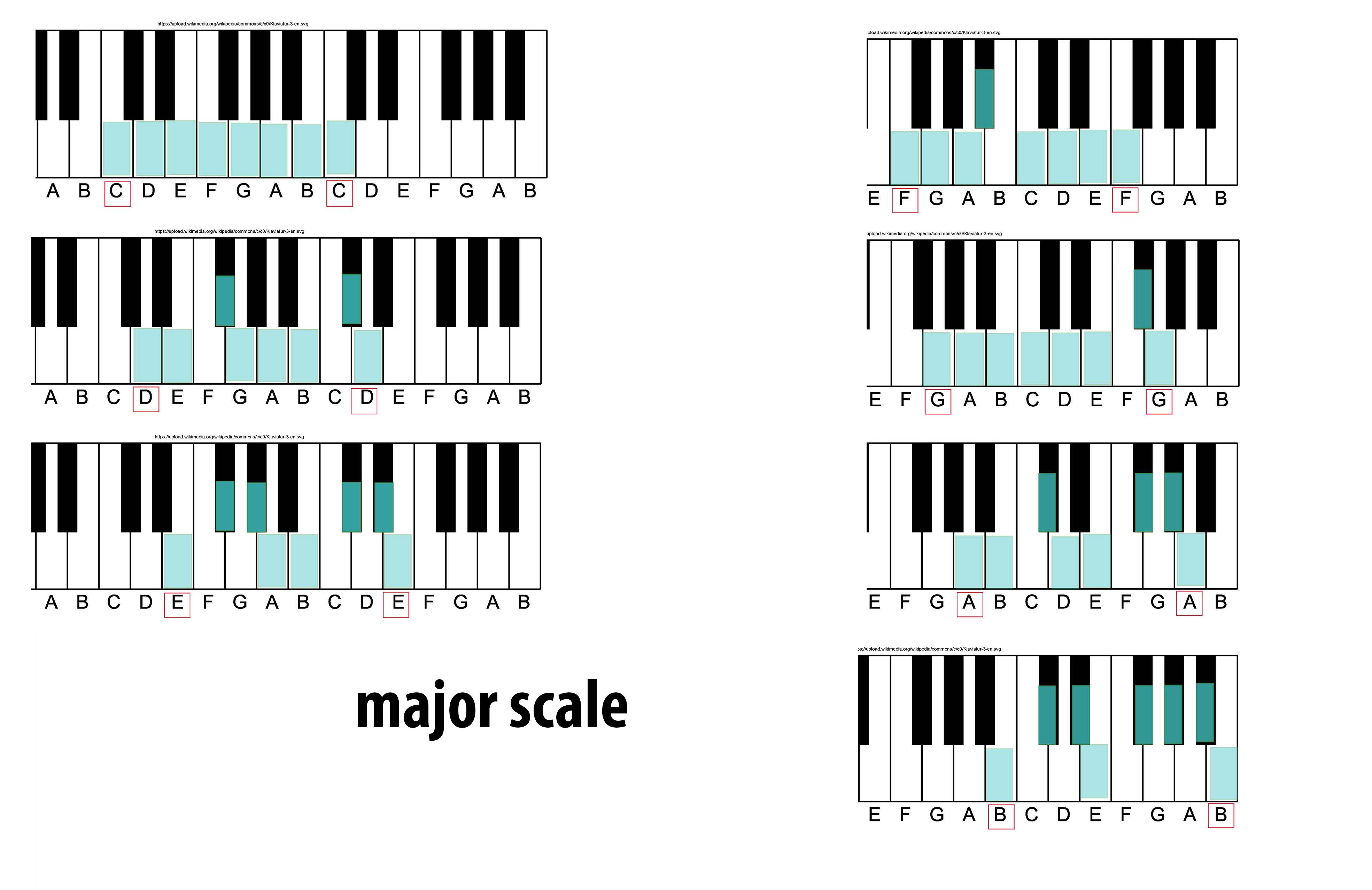
Major Scale
The major scale (or Ionian mode) is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double its frequency so that it is called a higher octave of the same note (from Latin "octavus", the eighth). The simplest major scale to write is C major, the only major scale not requiring sharps or flats: The major scale has a central importance in Western music, particularly that of the common practice period and in popular music. In Carnatic music, it is known as '' Sankarabharanam''. In Hindustani classical music, it is known as '' Bilaval''. Structure A major scale is a diatonic scale. The sequence of intervals between the notes of a major scale is: : whole, whole, half, whole, whole, whole, half where "whole" stands for a whole tone (a red u-shaped curve in the figure), and "half" stands for a semitone (a red angled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, ..., the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemy, Ptolemaic comma, or the diatonic comma is a small Comma (music), comma type interval (music), interval between two musical notes, equal to the frequency ratio (= 1.0125) (around 21.51 cent (music), cents). Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a ''Didymean comma'' because it is the amount by which Didymus the Musician, Didymus corrected the Pythagorean interval, Pythagorean major thir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ditone
In music, a ditone (, from , "of two tones") is the interval of a major third. The size of a ditone varies according to the sizes of the two tones of which it is compounded. The largest is the Pythagorean ditone, with a ratio of 81:64, also called a comma-redundant major third; the smallest is the interval with a ratio of 100:81, also called a comma-deficient major third. Pythagorean tuning The Pythagorean ditone is the major third in Pythagorean tuning, which has an interval ratio of 81:64, which is 407.82 cents. The Pythagorean ditone is evenly divisible by two major tones (9/8 or 203.91 cents) and is wider than a just major third (5/4, 386.31 cents) by a syntonic comma (81/80, 21.51 cents). Because it is a comma wider than a "perfect" major third of 5:4, it is called a "comma-redundant" interval. "The major third that appears commonly in the ythagoreansystem (C–E, D–F, etc.) is more properly known as the Pythagorean ditone and consists of two major and two minor semi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, to check intonation, or to compare the sizes of comparable intervals in different tuning systems. For humans, a single cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, \sqrt 200/math>, at Robert Holford Macdowell Bosanquet's suggestion. Making extensive measurements of musical instruments from around the world, Ellis used cents to report and compare the scales employed, and further described and utilized the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semitone
A semitone, also called a minor second, half step, or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale (or half of a whole step), visually seen on a keyboard as the distance between two keys that are adjacent to each other. For example, C is adjacent to C; the interval between them is a semitone. In a 12-note approximately equally divided scale, any interval can be defined in terms of an appropriate number of semitones (e.g. a whole tone or major second is 2 semitones wide, a major third 4 semitones, and a perfect fifth 7 semitones). In music theory, a distinction is made between a diatonic semitone, or minor second (an interval encompassing two different staff positions, e.g. from C to D) and a chromatic semitone or augmented unison (an interval between two notes at the same staff position, e.g. f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12 Equal Temperament
12 equal temperament (12-ET) is the musical system that divides the octave into 12 parts, all of which are Equal temperament, equally tempered (equally spaced) on a logarithmic scale, with a ratio equal to the Twelfth root of two, 12th root of 2 (\sqrt[12] ≈ 1.05946). That resulting smallest interval, the width of an octave, is called a semitone or half step. Twelve-tone equal temperament is the most widespread system in music today. It has been the predominant tuning system of Western music, starting with classical music, since the 18th century, and Europe almost exclusively used approximations of it for millennia before that. It has also been used in other cultures. In modern times, 12-ET is usually tuned relative to a standard pitch of 440 Hz, called A440 (pitch standard), A440, meaning one note, A (musical note), A4 (the A in the 4th octave of a typical 88-key piano), is tuned to 440 hertz and all other notes are defined as some multiple of semitones apart from it, ei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Cents
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, to check intonation, or to compare the sizes of comparable intervals in different tuning systems. For humans, a single cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, \sqrt 200/math>, at Robert Holford Macdowell Bosanquet's suggestion. Making extensive measurements of musical instruments from around the world, Ellis used cents to report and compare the scales employed, and further described and utilized the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Intonation
In music, just intonation or pure intonation is a musical tuning, tuning system in which the space between notes' frequency, frequencies (called interval (music), intervals) is a natural number, whole number ratio, ratio. Intervals spaced in this way are said to be pure, and are called just intervals. Just intervals (and chords created by combining them) consist of tones from a single harmonic series (music), harmonic series of an implied fundamental frequency, fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth (music), fourth. In Western musical practice, bowed instruments such as violins, violas, cellos, and double basses are tuned using pure fifths or fourths. In contrast, keyboard instruments are rarely tuned using only pure intervals—the desire fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Tuning
In music, there are two common meanings for tuning: * #Tuning practice, Tuning practice, the act of tuning an instrument or voice. * #Tuning systems, Tuning systems, the various systems of Pitch (music), pitches used to tune an instrument, and their theoretical bases. Tuning practice Tuning is the process of adjusting the pitch of one or many tones from musical instruments to establish typical intervals between these tones. Tuning is usually based on a fixed reference, such as A440 (pitch standard), A = 440 Hz. The term "''out of tune''" refers to a pitch/tone that is either too high (Sharp (music), sharp) or too low (Flat (music), flat) in relation to a given reference pitch. While an instrument might be in tune relative to its own range of notes, it may not be considered 'in tune' if it does not match the chosen reference pitch. Some instruments become 'out of tune' with temperature, humidity, damage, or simply time, and must be readjusted or repaired. Different method ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of the first five consecutive Musical note, notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the Tritone, diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the Harmonic series (music), harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant (music), dominant note is a perfect fifth above the tonic (music), tonic note. The perfect fifth is more consonance and dissonance, consonant, or stable, than any other interval except the unison and the octave. It occu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root (chord)
In the music theory of harmony, the root is a specific Note (music), note that names and typifies a given chord (music), chord. Chords are often spoken about in terms of their root, their Chord quality, quality, and their Chord extensions, extensions. When a chord is named without reference to quality, it is assumed to be major chord, major—for example, a "C chord" refers to a C major triad, containing the notes C, E, and G. In a given harmonic context, the root of a chord need not be in bass note, the bass position, as chords may be Inversion (music), inverted while retaining the same name, and therefore the same root. In tertian harmonic theory, wherein chords can be considered stacks of third intervals (e.g. in common practice period, common practice tonality), the root of a chord is the Musical note, note on which the subsequent thirds are stacked. For instance, the root of a triad (music), triad such as E Minor is E, independently of the vertical order in which the three n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |