|
Intersection (geometry)
In geometry, an intersection is a point, line, or curve common to two or more objects (such as lines, curves, planes, and surfaces). The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point (sometimes called a '' vertex'') or does not exist (if the lines are parallel). Other types of geometric intersection include: * Line–plane intersection * Line–sphere intersection * Intersection of a polyhedron with a line * Line segment intersection * Intersection curve Determination of the intersection of flats – linear geometric objects embedded in a higher-dimensional space – is a simple task of linear algebra, namely the solution of a system of linear equations. In general the determination of an intersection leads to non-linear equations, which can be solved numerically, for example using Newton iteration. Intersection problems between a line and a conic section (circle, ellipse, parabola, etc.) or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line–line Intersection
In Euclidean geometry, the intersection of a line and a line can be the empty set, a point (geometry), point, or another Line (geometry), line. Distinguishing these cases and finding the Intersection (Euclidean geometry), intersection have uses, for example, in computer graphics, motion planning, and collision detection. In three-dimensional Euclidean geometry, if two lines are not in the same plane (geometry), plane, they have no point of intersection and are called skew lines. If they are in the same plane, however, there are three possibilities: if they coincide (are not distinct lines), they have an infinitude of points in common (namely all of the points on either of them); if they are distinct but have the same slope, they are said to be parallel (geometry), parallel and have no points in common; otherwise, they have a single point of intersection. The distinguishing features of non-Euclidean geometry are the number and locations of possible intersections between two lines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
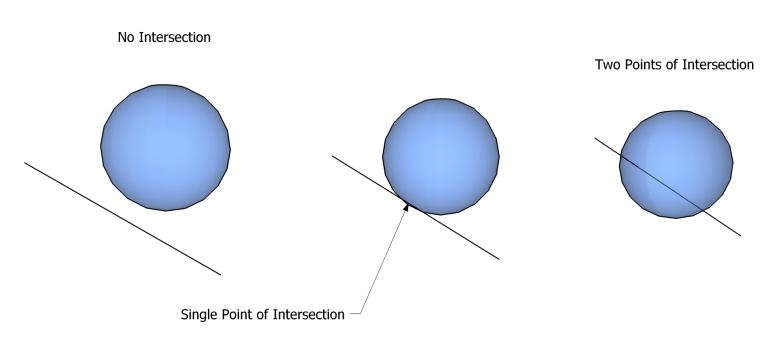
Line–sphere Intersection
In analytic geometry, a line and a sphere can intersect in three ways: # No intersection at all # Intersection in exactly one point # Intersection in two points. Methods for distinguishing these cases, and determining the coordinates for the points in the latter cases, are useful in a number of circumstances. For example, it is a common calculation to perform during ray tracing. Calculation using vectors in 3D In vector notation, the equations are as follows: Equation for a sphere :\left\Vert \mathbf - \mathbf \right\Vert^2=r^2 :*\mathbf : points on the sphere :*\mathbf : center point :*r : radius of the sphere Equation for a line starting at \mathbf :\mathbf=\mathbf + d\mathbf :*\mathbf : points on the line :*\mathbf : origin of the line :*d : distance from the origin of the line :*\mathbf : direction of line (a non-zero vector) Searching for points that are on the line and on the sphere means combining the equations and solving for d, involving the dot product of vector ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Solution
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two Lines
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and the only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures. Mathematics The number 2 is the second natural number after 1. Each natural number, including 2, is constructed by succession, that is, by adding 1 to the previous natural number. 2 is the smallest and the only even prime number, and the first Ramanujan prime. It is also the first superior highly composite number, and the first colossally abundant number. An integer is determined to be even if it is divisible by two. When written in base 10, all multiples of 2 will end in 0, 2, 4, 6, or 8; more generally, in any even base, even numbers will end with an even digit. A digon is a polygon with two sides (or edges) and two vertices. Two distinct points in a plane are always sufficient to define a unique line in a nontri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cramer's Rule
In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution. It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-sides of the equations. It is named after Gabriel Cramer, who published the rule for an arbitrary number of unknowns in 1750, although Colin Maclaurin also published special cases of the rule in 1748, and possibly knew of it as early as 1729. Cramer's rule, implemented in a naive way, is computationally inefficient for systems of more than two or three equations. In the case of equations in unknowns, it requires computation of determinants, while Gaussian elimination produces the result with the same (up to a constant factor independent of ) computational complexity as the computation of a single determinant. Moreo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form P = 0, where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For example, x^5-3x+1=0 is an algebraic equation with integer coefficients and :y^4 + \frac - \frac + xy^2 + y^2 + \frac = 0 is a multivariate polynomial equation over the rationals. For many authors, the term ''algebraic equation'' refers only to the univariate case, that is polynomial equations that involve only one variable. On the other hand, a polynomial equation may involve several variables (the ''multivariate'' case), in which case the term ''polynomial equation'' is usually preferred. Some but not all polynomial equations with rational coefficients have a solution that is an algebraic expression that can be found using a finite number of operations that involve only those same types of coefficients (that is, can be solved algebraically). This can be done for all such eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartic Equation
In mathematics, a quartic equation is one which can be expressed as a ''quartic function'' equaling zero. The general form of a quartic equation is :ax^4+bx^3+cx^2+dx+e=0 \, where ''a'' ≠ 0. The quartic is the highest order polynomial equation that can be solved by radicals in the general case. History Lodovico Ferrari is attributed with the discovery of the solution to the quartic in 1540, but since this solution, like all algebraic solutions of the quartic, requires the solution of a cubic to be found, it could not be published immediately. The solution of the quartic was published together with that of the cubic by Ferrari's mentor Gerolamo Cardano in the book '' Ars Magna'' (1545). The proof that this was the highest order general polynomial for which such solutions could be found was first given in the Abel–Ruffini theorem in 1824, proving that all attempts at solving the higher order polynomials would be futile. The notes left by Évariste Galois before ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |