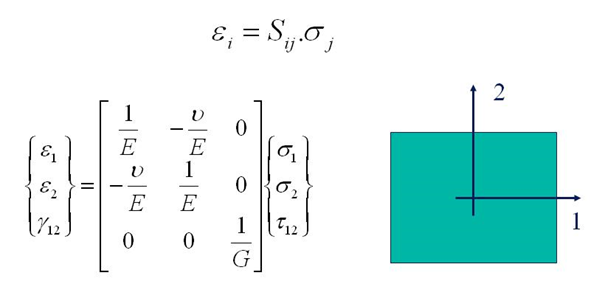|
Impulse Excitation Technique
The impulse excitation technique (IET) is a non-destructive material characterization technique to determine the elastic properties and internal friction of a material of interest. It measures the resonant frequencies in order to calculate the Young's modulus, shear modulus, Poisson's ratio and internal friction of predefined shapes like rectangular bars, cylindrical rods and disc shaped samples. The measurements can be performed at room temperature or at elevated temperatures (up to 1700 °C) under different atmospheres. The measurement principle is based on tapping the sample with a small projectile and recording the induced vibration signal with a piezoelectric sensor, microphone, laser vibrometer or accelerometer. To optimize the results a microphone or a laser vibrometer can be used as there is no contact between the test-piece and the sensor. Laser vibrometers are preferred to measure signals in vacuum. Afterwards, the acquired vibration signal in the time domain is co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Frequency
The fundamental frequency, often referred to simply as the ''fundamental'' (abbreviated as 0 or 1 ), is defined as the lowest frequency of a Periodic signal, periodic waveform. In music, the fundamental is the musical pitch (music), pitch of a note that is perceived as the lowest Harmonic series (music)#Partial, partial present. In terms of a superposition of Sine wave, sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency Zero-based numbering, counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc.) According to Benward and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropy
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthotropic
Orthotropic may refer to: * Orthotropic material is one that has different material properties or strengths in different orthogonal directions (e.g., glass-reinforced plastic, or wood) * Orthotropic deck, in bridge design, is one made from solid steel plate * Orthotropic movement, in botany, is a type of tropism In biology, a tropism is a phenomenon indicating the growth or turning movement of an organism, usually a plant, in response to an environmental stimulus (physiology), stimulus. In tropisms, this response is dependent on the direction of the s ... along the same axis as the stimulus * Orthotropics, a method claimed to be able to guide facial growth {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthotropic Material
In material science and solid mechanics, orthotropic materials have material properties at a particular point which differ along three orthogonal axes, where each axis has twofold rotational symmetry. These directional differences in strength can be quantified with Hankinson's equation. They are a subset of anisotropic materials, because their properties change when measured from different directions. A familiar example of an orthotropic material is wood. In wood, one can define three mutually perpendicular directions at each point in which the properties are different. It is most stiff (and strong) along the grain (axial direction), because most cellulose fibrils are aligned that way. It is usually least stiff in the radial direction (between the growth rings), and is intermediate in the circumferential direction. This anisotropy was provided by evolution, as it best enables the tree to remain upright. Because the preferred coordinate system is cylindrical-polar, this type of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Stress
Shear stress (often denoted by , Greek alphabet, Greek: tau) is the component of stress (physics), stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. ''Normal stress'', on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts. General shear stress The formula to calculate average shear stress or force per unit area is: \tau = ,where is the force applied and is the cross-sectional area. The area involved corresponds to the material face (geometry), face parallel to the applied force vector, i.e., with surface normal vector perpendicular to the force. Other forms Wall shear stress Wall shear stress expresses the retarding force (per unit area) from a wall in the layers of a fluid flowing next to the wall. It is defined as:\tau_w := \mu\left.\frac\_,where is the dynamic viscosity, is the flow velocity, and is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic Stress Strain Relation
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an isotropi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damped Sin
In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include viscous damping in a fluid (see viscous drag), surface friction, radiation, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Damping is not to be confused with friction, which is a type of dissipative force acting on a system. Friction can cause or be a factor of damping. Many systems exhibit oscillatory behavior when they are disturbed from their position of static equilibrium. A mass suspended from a spring, for example, might, if pulled and released, bounce up and down. On each bounce, the system tends to return to its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quality Control
Quality control (QC) is a process by which entities review the quality of all factors involved in production. ISO 9000 defines quality control as "a part of quality management focused on fulfilling quality requirements". This approach places emphasis on three aspects (enshrined in standards such as ISO 9001): # Elements such as controls, job management, defined and well managed processes, performance and integrity criteria, and identification of records # Competence, such as knowledge, skills, experience, and qualifications # Soft elements, such as personnel, integrity, confidence, organizational culture, motivation, team spirit, and quality relationships. Inspection is a major component of quality control, where physical product is examined visually (or the end results of a service are analyzed). Product inspectors will be provided with lists and descriptions of unacceptable product defects such as cracks or surface blemishes for example. History and introductio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Refractory
In materials science, a refractory (or refractory material) is a material that is resistant to decomposition by heat or chemical attack and that retains its strength and rigidity at high temperatures. They are inorganic, non-metallic compounds that may be porous or non-porous, and their crystallinity varies widely: they may be crystalline, polycrystalline, amorphous, or composite. They are typically composed of oxides, carbides or nitrides of the following elements: silicon, aluminium, magnesium, calcium, boron, chromium and zirconium. Many refractories are ceramics, but some such as graphite are not, and some ceramics such as clay pottery are not considered refractory. Refractories are distinguished from the '' refractory metals'', which are elemental metals and their alloys that have high melting temperatures. Refractories are defined by ASTM C71 as "non-metallic materials having those chemical and physical properties that make them applicable for structures, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ceramic Engineering
Ceramic engineering is the science and technology of creating objects from inorganic, non-metallic materials. This is done either by the action of heat, or at lower temperatures using precipitation reactions from high-purity chemical solutions. The term includes the purification of raw materials, the study and production of the chemical compounds concerned, their formation into components and the study of their structure, composition and properties. Ceramic materials may have a crystalline or partly crystalline structure, with long-range order on atomic scale. Glass-ceramics may have an amorphous or glassy structure, with limited or short-range atomic order. They are either formed from a molten mass that solidifies on cooling, formed and matured by the action of heat, or chemically synthesized at low temperatures using, for example, hydrothermal or sol-gel synthesis. The special character of ceramic materials gives rise to many applications in materials engineering, electri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultrasound Spectroscopy
Ultrasound is sound with frequencies greater than 20 kilohertz. This frequency is the approximate upper audible limit of human hearing in healthy young adults. The physical principles of acoustic waves apply to any frequency range, including ultrasound. Ultrasonic devices operate with frequencies from 20 kHz up to several gigahertz. Ultrasound is used in many different fields. Ultrasonic devices are used to detect objects and measure distances. Ultrasound imaging or sonography is often used in medicine. In the nondestructive testing of products and structures, ultrasound is used to detect invisible flaws. Industrially, ultrasound is used for cleaning, mixing, and accelerating chemical processes. Animals such as bats and porpoises use ultrasound for locating prey and obstacles. History Acoustics, the science of sound, starts as far back as Pythagoras in the 6th century BC, who wrote on the mathematical properties of stringed instruments. Echolocation in bats was d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |