|
Geocentric Gravitational Constant
In celestial mechanics, the standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of the bodies. For two bodies the parameter may be expressed as G(m1+m2), or as GM when one body is much larger than the other. \mu=GM \ For several objects in the Solar System, the value of ''μ'' is known to greater accuracy than either ''G'' or ''M''. The SI units of the standard gravitational parameter are . However, units of are frequently used in the scientific literature and in spacecraft navigation. Definition Small body orbiting a central body The central body in an orbital system can be defined as the one whose mass (''M'') is much larger than the mass of the orbiting body (''m''), or . This approximation is standard for planets orbiting the Sun or most moons and greatly simplifies equations. Under Newton's law of universal gravitation, if the distance between the bodies is ''r'', the force exerted on the sm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mercury (planet)
Mercury is the smallest planet in the Solar System and the closest to the Sun. Its orbit around the Sun takes 87.97 Earth days, the shortest of all the Sun's planets. It is named after the Roman god ' ( Mercury), god of commerce, messenger of the gods, and mediator between gods and mortals, corresponding to the Greek god Hermes (). Like Venus, Mercury orbits the Sun within Earth's orbit as an inferior planet, and its apparent distance from the Sun as viewed from Earth never exceeds 28°. This proximity to the Sun means the planet can only be seen near the western horizon after sunset or the eastern horizon before sunrise, usually in twilight. At this time, it may appear as a bright star-like object, but is more difficult to observe than Venus. From Earth, the planet telescopically displays the complete range of phases, similar to Venus and the Moon, which recurs over its synodic period of approximately 116 days. The synodic proximity of Mercury to Earth makes Mercury mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metre
The metre (British spelling) or meter (American spelling; see spelling differences) (from the French unit , from the Greek noun , "measure"), symbol m, is the primary unit of length in the International System of Units (SI), though its prefixed forms are also used relatively frequently. The metre was originally defined in 1793 as one ten-millionth of the distance from the equator to the North Pole along a great circle, so the Earth's circumference is approximately km. In 1799, the metre was redefined in terms of a prototype metre bar (the actual bar used was changed in 1889). In 1960, the metre was redefined in terms of a certain number of wavelengths of a certain emission line of krypton-86. The current definition was adopted in 1983 and modified slightly in 2002 to clarify that the metre is a measure of proper length. From 1983 until 2019, the metre was formally defined as the length of the path travelled by light in a vacuum in of a second. After the 2019 redefiniti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
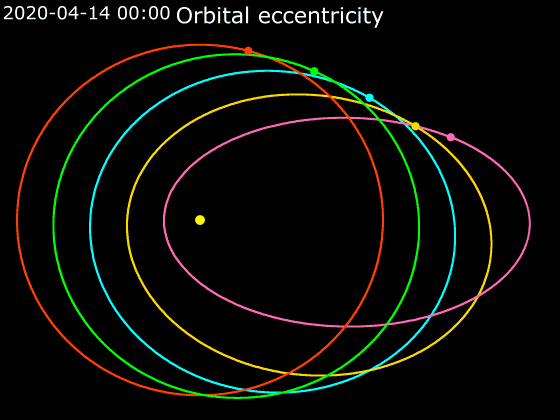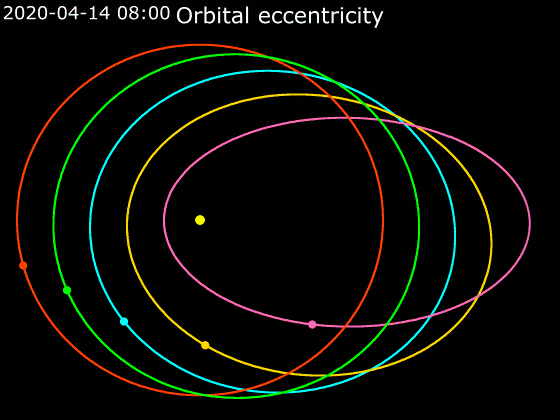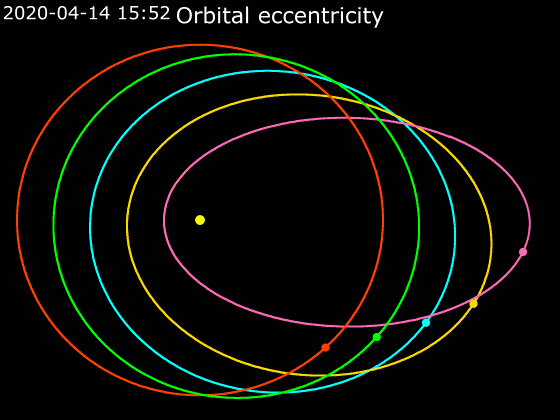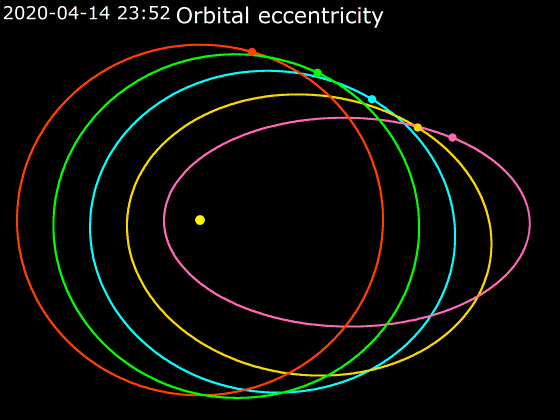
Kepler's Laws Of Planetary Motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the cente ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Orbit
In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 (thus excluding the circular orbit). In a wider sense, it is a Kepler's orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1. In a gravitational two-body problem with negative energy, both bodies follow similar elliptic orbits with the same orbital period around their common barycenter. Also the relative position of one body with respect to the other follows an elliptic orbit. Examples of elliptic orbits include: Hohmann transfer orbit, Molniya orbit, and tundra orbit. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies m1 and m2, the orbital speed (v\,) of one bod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Period
The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. For celestial objects in general, the sidereal period ( sidereal year) is referred to by the orbital period, determined by a 360° revolution of one body around its primary, e.g. Earth around the Sun, relative to the fixed stars projected in the sky. Orbital periods can be defined in several ways. The tropical period is more particularly about the position of the parent star. It is the basis for the solar year, and respectively the calendar year. The synodic period incorporates not only the orbital relation to the parent star, but also to other celestial objects, making it not a mere different approach to the orbit of an object around its parent, but a period of orbital relations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Speed
Angular may refer to: Anatomy * Angular artery, the terminal part of the facial artery * Angular bone, a large bone in the lower jaw of amphibians and reptiles * Angular incisure, a small anatomical notch on the stomach * Angular gyrus, a region of the brain in the parietal lobe * Angular vein, formed by the junction of the frontal vein and supraorbital vein Other uses * Angular (web framework), an open-source web platform ** AngularJS, the first incarnation of Angular * Angle, having an angle or angles * Angular diameter The angular diameter, angular size, apparent diameter, or apparent size is an angular distance describing how large a sphere or circle appears from a given point of view. In the vision sciences, it is called the visual angle, and in optics, it is ..., describing how large a sphere or circle appears from a given point of view ** Angular diameter distance, used in astronomy * Angular Recording Corporation, a British independent record label See also * Ang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Speed
In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body. The term can be used to refer to either the mean orbital speed (i.e. the average speed over an entire orbit) or its instantaneous speed at a particular point in its orbit. The maximum (instantaneous) orbital speed occurs at periapsis (perigee, perihelion, etc.), while the minimum speed for objects in closed orbits occurs at apoapsis (apogee, aphelion, etc.). In ideal two-body systems, objects in open orbits continue to slow down forever as their distance to the barycenter increases. When a system approximates a two-body system, instantaneous orbital speed at a given point of the orbit can be computed from its distance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the spoke of a chariot wheel. as a function of axial position ../nowiki>" Spherical coordinates In a spherical coordinate system, the radius describes the distance of a point from a fixed origin. Its position if further defined by the polar angle measured between the radial direction and a fixed zenith direction, and the azimuth angle, the angle between the orthogonal projection of the radial direction on a reference plane that passes through the origin and is orthogonal to the zenith, and a fixed reference direction in that plane. See also *Bend radius *Filling radius in Riemannian geometry *Radius of convergence *Radius of convexity * Radius of curvature *Radius of gyration ''Radius of gyration'' or gyradius of a body about the axis of ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. Listed below is a circular orbit in astrodynamics or celestial mechanics under standard assumptions. Here the centripetal force is the gravitational force, and the axis mentioned above is the line through the center of the central mass perpendicular to the plane of motion. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version. Circular acceleration Transverse acceleration (perpendicular to velocity) causes change in direction. If it is constant in magnitude and changing in direction with the velocity, circular motion ensues. Taking two derivatives of the particle's coordinates with respect to time gives the centripetal acceleration : a\, = \frac \, = where: *v\, is orbital velocity of orbiting body, *r\, is radius of the cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Law Of Universal Gravitation
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers.It was shown separately that separated spherically symmetrical masses attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the " first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors. This is a general physical law derived from empirical observations by what Isaac Newton called inductive reasoning. It is a part of classical mechanics and was formulated in Newton's work '' Philosophiæ Naturalis Principia Mathematica'' ("the ''Principia''"), first published on 5 July 1687. When Newton presented Book 1 of the unpublished text in April 1686 to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbiting Body
In astrodynamics, an orbiting body is any physical body that orbits a more massive one, called the primary body. The orbiting body is properly referred to as the secondary body (m_2), which is less massive than the primary body (m_1). Thus, m_2 m_2. Under standard assumptions in astrodynamics, the barycenter of the two bodies is a focus of both orbits. An orbiting body may be a spacecraft (i.e. an artificial satellite) or a natural satellite, such as a planet, dwarf planet, moon, moonlet, asteroid, or comet. A system of two orbiting bodies is modeled by the Two-Body Problem and a system of three orbiting bodies is modeled by the Three-Body Problem. These problems can be generalized to an N-body problem. While there are a few analytical solutions to the n-body problem, it can be reduced to a 2-body system if the secondary body stays out of other bodies' Sphere of Influence and remains in the primary body's sphere of influence. See also * Barycenter * Double planet *Pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |