|
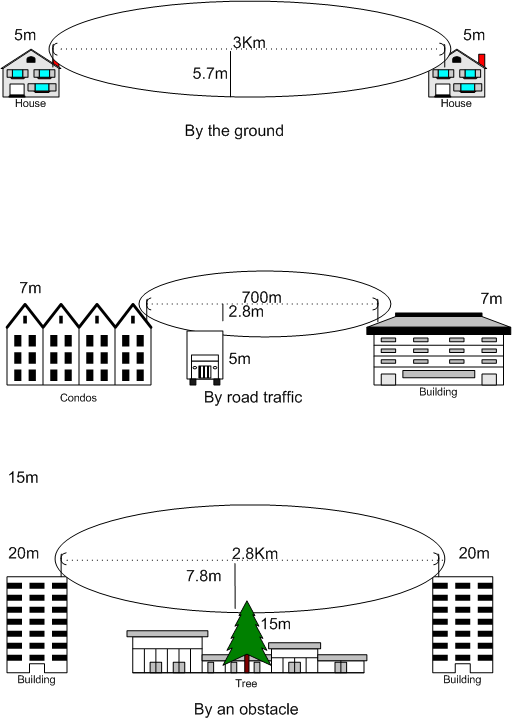
Fresnel Zone
A Fresnel zone ( ), named after physicist Augustin-Jean Fresnel, is one of a series of confocal prolate ellipsoidal regions of space between and around a transmitter and a receiver. The primary wave will travel in a relative straight line from the transmitter to the receiver. Aberrant transmitted radio, sound, or light waves which are transmitted at the same time can follow slightly different paths before reaching a receiver, especially if there are obstructions or deflecting objects between the two. The two waves can arrive at the receiver at slightly different times and the aberrant wave may arrive out of phase with the primary wave due to the different path lengths. Depending on the magnitude of the phase difference between the two waves, the waves can interfere constructively or destructively. The size of the calculated Fresnel zone at any particular distance from the transmitter and receiver can help to predict whether obstructions or discontinuities along the path w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fresnel Zone Disrupted
Augustin-Jean Fresnel (10 May 1788 – 14 July 1827) was a French civil engineer and physicist whose research in optics led to the almost unanimous acceptance of the wave theory of light, excluding any remnant of Newton's corpuscular theory, from the late 1830s until the end of the 19th century. He is perhaps better known for inventing the catadioptric (reflective/refractive) Fresnel lens and for pioneering the use of "stepped" lenses to extend the visibility of lighthouses, saving countless lives at sea. The simpler dioptric (purely refractive) stepped lens, first proposed by Count Buffon and independently reinvented by Fresnel, is used in screen magnifiers and in condenser lenses for overhead projectors. By expressing Christiaan Huygens, Huygens's principle of secondary waves and Thomas Young (scientist), Young's principle of interference (wave propagation), interference in quantitative terms, and supposing that simple colors consist of sine wave, sinusoidal waves, Fre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipath Propagation
In radio communication, multipath is the propagation phenomenon that results in radio signals reaching the receiving antenna by two or more paths. Causes of multipath include atmospheric ducting, ionospheric reflection and refraction, and reflection from water bodies and terrestrial objects such as mountains and buildings. When the same signal is received over more than one path, it can create interference and phase shifting of the signal. Destructive interference causes fading; this may cause a radio signal to become too weak in certain areas to be received adequately. For this reason, this effect is also known as multipath interference or multipath distortion. Where the magnitudes of the signals arriving by the various paths have a distribution known as the Rayleigh distribution, this is known as Rayleigh fading. Where one component (often, but not necessarily, a line of sight component) dominates, a Rician distribution provides a more accurate model, and this is known a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex (curve)
In the geometry of plane curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature, and some authors define a vertex to be more specifically a local extremum of curvature. However, other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant. For space curves, on the other hand, a vertex is a point where the torsion vanishes. Examples A hyperbola has two vertices, one on each branch; they are the closest of any two points lying on opposite branches of the hyperbola, and they lie on the principal axis. On a parabola, the sole vertex lies on the axis of symmetry and in a quadratic of the form: :ax^2 + bx + c\,\! it can be found by completing the square or by differentiation., p. 127. On an ellipse, two of the four vertices lie on the major axis and two lie on the minor axis. For a circle, which has constant curvature, every point is a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Approximation
The binomial approximation is useful for approximately calculating powers of sums of 1 and a small number ''x''. It states that : (1 + x)^\alpha \approx 1 + \alpha x. It is valid when , x, -1 and \alpha \geq 1. Derivations Using linear approximation The function : f(x) = (1 + x)^ is a smooth function for ''x'' near 0. Thus, standard linear approximation tools from calculus apply: one has : f'(x) = \alpha (1 + x)^ and so : f'(0) = \alpha. Thus : f(x) \approx f(0) + f'(0)(x - 0) = 1 + \alpha x. By Taylor's theorem, the error in this approximation is equal to \frac \cdot (1 + \zeta)^ for some value of \zeta that lies between 0 and . For example, if x < 0 and , the error is at most . In little o notation, one can say that the error is , meaning that |
Wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats. It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings, and is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter '' lambda'' (λ). The term ''wavelength'' is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids. Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths. Wavelength depends on the medium (for example, vacuum, air, or water) tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rule Of Thumb
In English, the phrase ''rule of thumb'' refers to an approximate method for doing something, based on practical experience rather than theory. This usage of the phrase can be traced back to the 17th century and has been associated with various trades where quantities were measured by comparison to the width or length of a thumb. A modern folk etymology holds that the phrase is derived from the maximum width of a stick allowed for wife-beating under English common law, but no such law ever existed. This belief may have originated in a rumored statement by 18th-century judge Sir Francis Buller that a man may beat his wife with a stick no wider than his thumb. The rumor produced numerous jokes and satirical cartoons at Buller's expense, but there is no record that he made such a statement. English jurist Sir William Blackstone wrote in his ''Commentaries on the Laws of England'' of an "old law" that once allowed "moderate" beatings by husbands, but he did not mention thumbs or an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interference (communication)
In telecommunications, an interference is that which modifies a signal in a disruptive manner, as it travels along a communication channel between its source and receiver. The term is often used to refer to the addition of unwanted signals to a useful signal. Common examples include: * Electromagnetic interference (EMI) * Co-channel interference (CCI), also known as crosstalk * Adjacent-channel interference (ACI) * Intersymbol interference (ISI) * Inter-carrier interference (ICI), caused by doppler shift in OFDM modulation (multitone modulation). * Common-mode interference (CMI) * Conducted interference Noise is a form of interference but not all interference is noise. Radio resource management aims at reducing and controlling the co-channel and adjacent-channel interference. Interference alignment A solution to interference problems in wireless communication networks is interference alignment, which was crystallized by Syed Ali Jafar at the University of California, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line-of-sight Propagation
Line-of-sight propagation is a characteristic of electromagnetic radiation or acoustic wave propagation which means waves travel in a direct path from the source to the receiver. Electromagnetic transmission includes light emissions traveling in a straight line. The rays or waves may be diffracted, refracted, reflected, or absorbed by the atmosphere and obstructions with material and generally cannot travel over the horizon or behind obstacles. In contrast to line-of-sight propagation, at low frequency (below approximately 3 MHz) due to diffraction, radio waves can travel as ground waves, which follow the contour of the Earth. This enables AM radio stations to transmit beyond the horizon. Additionally, frequencies in the shortwave bands between approximately 1 and 30 MHz, can be refracted back to Earth by the ionosphere, called skywave or "skip" propagation, thus giving radio transmissions in this range a potentially global reach. However, at frequencies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal-to-noise Ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to the noise power, often expressed in decibels. A ratio higher than 1:1 (greater than 0 dB) indicates more signal than noise. SNR, bandwidth, and channel capacity of a communication channel are connected by the Shannon–Hartley theorem. Definition Signal-to-noise ratio is defined as the ratio of the power of a signal (meaningful input) to the power of background noise (meaningless or unwanted input): : \mathrm = \frac, where is average power. Both signal and noise power must be measured at the same or equivalent points in a system, and within the same system bandwidth. Depending on whether the signal is a constant () or a random variable (), the signal-to-noise ratio for random noise becomes: : \mathrm = \frac where E refers to the expected value, i.e. in this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave. In electrodynamics, the strength and direction of an electric field is defined by its electric field vector. In the case of a circularly polarized wave, as seen in the accompanying animation, the tip of the electric field vector, at a given point in space, relates to the phase of the light as it travels through time and space. At any instant of time, the electric field vector of the wave indicates a point on a helix oriented along the direction of propagation. A circularly polarized wave can rotate in one of two possible senses: clockwise or ''right-handed circular polarization (RHCP)'' in which the electric field vector rotates in a right-hand sense with respect to the direction of propagation, and counter-cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Shift
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \phi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \phi(t) is also a periodic function, with the same period as F, that repeatedly scans the same range o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |