|
Forward Difference Operator
A finite difference is a mathematical expression of the form . If a finite difference is divided by , one gets a difference quotient. The approximation of derivatives by finite differences plays a central role in finite difference methods for the numerical solution of differential equations, especially boundary value problems. The difference operator, commonly denoted \Delta is the operator that maps a function to the function \Delta /math> defined by :\Delta x)= f(x+1)-f(x). A difference equation is a functional equation that involves the finite difference operator in the same way as a differential equation involves derivatives. There are many similarities between difference equations and differential equations, specially in the solving methods. Certain recurrence relations can be written as difference equations by replacing iteration notation with finite differences. In numerical analysis, finite differences are widely used for approximating derivatives, and the term "fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Quotient
In single-variable calculus, the difference quotient is usually the name for the expression : \frac which when taken to the limit as ''h'' approaches 0 gives the derivative of the function ''f''. The name of the expression stems from the fact that it is the quotient of the difference of values of the function by the difference of the corresponding values of its argument (the latter is (''x'' + ''h'') - ''x'' = ''h'' in this case). The difference quotient is a measure of the average rate of change of the function over an interval (in this case, an interval of length ''h''). The limit of the difference quotient (i.e., the derivative) is thus the instantaneous rate of change. By a slight change in notation (and viewpoint), for an interval 'a'', ''b'' the difference quotient : \frac is called the mean (or average) value of the derivative of ''f'' over the interval 'a'', ''b'' This name is justified by the mean value theorem, which states that for a differentiable function ''f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal
In mathematics, an infinitesimal number is a quantity that is closer to zero than any standard real number, but that is not zero. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " infinity- th" item in a sequence. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another. Infinitesimal numbers were introduced in the development of calculus, in which the derivative was first conceived as a ratio of two infinitesimal quantities. This definition was not rigorously formalized. As calculus developed further, infinitesimals were replaced by limits, which can be calculated using the standard real numbers. Infinitesimals regained popularit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Expansion
In mathematics, an asymptotic expansion, asymptotic series or Poincaré expansion (after Henri Poincaré) is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular, often infinite, point. Investigations by revealed that the divergent part of an asymptotic expansion is latently meaningful, i.e. contains information about the exact value of the expanded function. The most common type of asymptotic expansion is a power series in either positive or negative powers. Methods of generating such expansions include the Euler–Maclaurin summation formula and integral transforms such as the Laplace and Mellin transforms. Repeated integration by parts will often lead to an asymptotic expansion. Since a '' convergent'' Taylor series fits the definition of asymptotic expansion as well, the phrase "asymptotic series" usually implies a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Transform
In combinatorics, the binomial transform is a sequence transformation (i.e., a transform of a sequence) that computes its forward differences. It is closely related to the Euler transform, which is the result of applying the binomial transform to the sequence associated with its ordinary generating function. Definition The binomial transform, ''T'', of a sequence, , is the sequence defined by :s_n = \sum_^n (-1)^k a_k. Formally, one may write :s_n = (Ta)_n = \sum_^n T_ a_k for the transformation, where ''T'' is an infinite-dimensional operator with matrix elements ''T''''nk''. The transform is an involution, that is, :TT = 1 or, using index notation, :\sum_^\infty T_T_ = \delta_ where \delta_ is the Kronecker delta. The original series can be regained by :a_n=\sum_^n (-1)^k s_k. The binomial transform of a sequence is just the ''n''th forward differences of the sequence, with odd differences carrying a negative sign, namely: :\begin s_0 &= a_0 \\ s_1 &= - (\Delta a) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be ''finite'', as in these examples, or ''infi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal's Triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy. The rows of Pascal's triangle are conventionally enumerated starting with row n = 0 at the top (the 0th row). The entries in each row are numbered from the left beginning with k = 0 and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas the numbers 1 and 3 in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Coefficient
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is written \tbinom. It is the coefficient of the term in the polynomial expansion of the binomial power ; this coefficient can be computed by the multiplicative formula :\binom nk = \frac, which using factorial notation can be compactly expressed as :\binom = \frac. For example, the fourth power of is :\begin (1 + x)^4 &= \tbinom x^0 + \tbinom x^1 + \tbinom x^2 + \tbinom x^3 + \tbinom x^4 \\ &= 1 + 4x + 6 x^2 + 4x^3 + x^4, \end and the binomial coefficient \tbinom =\tfrac = \tfrac = 6 is the coefficient of the term. Arranging the numbers \tbinom, \tbinom, \ldots, \tbinom in successive rows for n=0,1,2,\ldots gives a triangular array called Pascal's triangle, satisfying the recurrence relation :\binom = \binom + \binom. The binomial coefficients occur in many areas of mathematics, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Derivative
In mathematics, the symmetric derivative is an operation generalizing the ordinary derivative. It is defined asThomson, p. 1. : \lim_ \frac. The expression under the limit is sometimes called the symmetric difference quotient. A function is said to be symmetrically differentiable at a point ''x'' if its symmetric derivative exists at that point. If a function is differentiable (in the usual sense) at a point, then it is also symmetrically differentiable, but the converse is not true. A well-known counterexample is the absolute value function , which is not differentiable at , but is symmetrically differentiable here with symmetric derivative 0. For differentiable functions, the symmetric difference quotient does provide a better numerical approximation of the derivative than the usual difference quotient. The symmetric derivative at a given point equals the arithmetic mean of the left and right derivatives at that point, if the latter two both exist. Neither Rolle's theorem nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
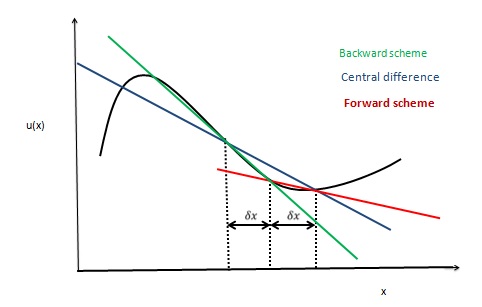
Central Difference Scheme
In applied mathematics, the central differencing scheme is a finite difference method that optimizes the approximation for the differential operator in the central node of the considered patch and provides numerical solutions to differential equations. It is one of the schemes used to solve the integrated convection–diffusion equation and to calculate the transported property Φ at the e and w faces, where ''e'' and ''w'' are short for ''east'' and ''west'' (compass directions being customarily used to indicate directions on computational grids). The method's advantages are that it is easy to understand and implement, at least for simple material relations; and that its convergence rate is faster than some other finite differencing methods, such as forward and backward differencing. The right side of the convection-diffusion equation, which basically highlights the diffusion terms, can be represented using central difference approximation. To simplify the solution and analysis, li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor's Theorem
In calculus, Taylor's theorem gives an approximation of a ''k''-times differentiable function around a given point by a polynomial of degree ''k'', called the ''k''th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order ''k'' of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial. Taylor's theorem is named after the mathematician Brook Taylor, who stated a version of it in 1715, although an earlier version of the result was already mentioned in 1671 by James Gregory. Taylor's theorem is taught in introductory-level calculus courses and is one of the central elementary tools in mathematical analysis. It gives simple arithmetic formula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Function
Although the function (sin ''x'')/''x'' is not defined at zero, as ''x'' becomes closer and closer to zero, (sin ''x'')/''x'' becomes arbitrarily close to 1. In other words, the limit of (sin ''x'')/''x'', as ''x'' approaches zero, equals 1. In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input. Formal definitions, first devised in the early 19th century, are given below. Informally, a function ''f'' assigns an output ''f''(''x'') to every input ''x''. We say that the function has a limit ''L'' at an input ''p,'' if ''f''(''x'') gets closer and closer to ''L'' as ''x'' moves closer and closer to ''p''. More specifically, when ''f'' is applied to any input ''sufficiently'' close to ''p'', the output value is forced ''arbitrarily'' close to ''L''. On the other hand, if some inputs very close to ''p'' are taken to outputs that stay a fixed distance apart, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |