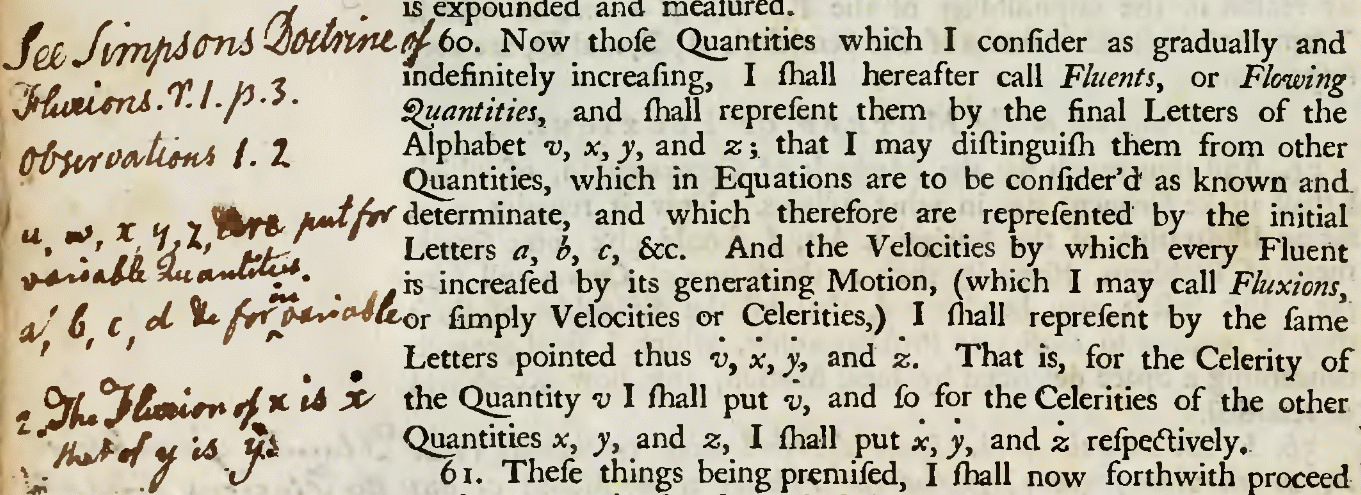|
Fluxion
A fluxion is the instantaneous rate of change, or gradient, of a fluent (a time-varying quantity, or function) at a given point. Fluxions were introduced by Isaac Newton to describe his form of a time derivative (a derivative with respect to time). Newton introduced the concept in 1665 and detailed them in his mathematical treatise, ''Method of Fluxions''. Fluxions and fluents made up Newton's early calculus. History Fluxions were central to the Leibniz–Newton calculus controversy, when Newton sent a letter to Gottfried Wilhelm Leibniz explaining them, but concealing his words in code due to his suspicion. He wrote: The gibberish string was in fact a hash code (by denoting the frequency of each letter) of the Latin phrase ''Data æqvatione qvotcvnqve flventes qvantitates involvente, flvxiones invenire: et vice versa'', meaning: "Given an equation that consists of any number of flowing quantities, to find the fluxions: and vice versa". Example If the fluent is defined as y=t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz–Newton Calculus Controversy
In the history of calculus, the calculus controversy (german: Prioritätsstreit, lit=priority dispute) was an argument between the mathematicians Isaac Newton and Gottfried Wilhelm Leibniz over who had first invented calculus. The question was a major intellectual controversy, which began simmering in 1699 and broke out in full force in 1711. Leibniz had published his work first, but Newton's supporters accused Leibniz of plagiarizing Newton's unpublished ideas. Leibniz died in disfavor in 1716 after his patron, the Elector Georg Ludwig of Hanover, became King George I of Great Britain in 1714. The modern consensus is that the two men developed their ideas independently. Newton said he had begun working on a form of calculus (which he called " the method of fluxions and fluents") in 1666, at the age of 23, but did not publish it except as a minor annotation in the back of one of his publications decades later (a relevant Newton manuscript of October 1666 is now published among ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Calculus
Calculus, originally called infinitesimal calculus, is a mathematical discipline focused on limits, continuity, derivatives, integrals, and infinite series. Many elements of calculus appeared in ancient Greece, then in China and the Middle East, and still later again in medieval Europe and in India. Infinitesimal calculus was developed in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz independently of each other. An argument over priority led to the Leibniz–Newton calculus controversy which continued until the death of Leibniz in 1716. The development of calculus and its uses within the sciences have continued to the present day. Etymology In mathematics education, ''calculus'' denotes courses of elementary mathematical analysis, which are mainly devoted to the study of functions and limits. The word ''calculus'' is Latin for "small pebble" (the diminutive of ''calx,'' meaning "stone"), a meaning which still persists in medicine. Because such pebbles were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Fluxions
''Method of Fluxions'' ( la, De Methodis Serierum et Fluxionum) is a mathematical treatise by Sir Isaac Newton which served as the earliest written formulation of modern calculus. The book was completed in 1671, and published in 1736. Fluxion is Newton's term for a derivative. He originally developed the method at Woolsthorpe Manor during the closing of Cambridge during the Great Plague of London from 1665 to 1667, but did not choose to make his findings known (similarly, his findings which eventually became the ''Philosophiae Naturalis Principia Mathematica'' were developed at this time and hidden from the world in Newton's notes for many years). Gottfried Leibniz developed his form of calculus independently around 1673, 7 years after Newton had developed the basis for differential calculus, as seen in surviving documents like “the method of fluxions and fluents..." from 1666. Leibniz however published his discovery of differential calculus in 1684, nine years before Newton f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluent (mathematics)
A fluent is a time-varying quantity or variable. The term was used by Isaac Newton in his early calculus to describe his form of a function. The concept was introduced by Newton in 1665 and detailed in his mathematical treatise, ''Method of Fluxions''. Newton described any variable that changed its value as a fluent – for example, the velocity of a ball thrown in the air. The derivative of a fluent is known as a fluxion, the main focus of Newton's calculus. A fluent can be found from its corresponding fluxion through integration. See also *''Method of Fluxions'' *History of calculus *Leibniz–Newton calculus controversy *Derivative *Newton's notation *Fluxion A fluxion is the instantaneous rate of change, or gradient, of a fluent (a time-varying quantity, or function) at a given point. Fluxions were introduced by Isaac Newton to describe his form of a time derivative (a derivative with respect to ti ... References {{Isaac Newton, state=collapsed Mathematical analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a "natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal
In mathematics, an infinitesimal number is a quantity that is closer to zero than any standard real number, but that is not zero. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " infinity- th" item in a sequence. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another. Infinitesimal numbers were introduced in the development of calculus, in which the derivative was first conceived as a ratio of two infinitesimal quantities. This definition was not rigorously formalized. As calculus developed further, infinitesimals were replaced by limits, which can be calculated using the standard real numbers. Infinitesimals regained popularit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. It has two major branches, differential calculus and integral calculus; the former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus, and they make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. Infinitesimal calculus was developed independently in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz. Later work, including (ε, δ)-definition of limit, codify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Notation
In differential calculus, there is no single uniform notation for differentiation. Instead, various notations for the derivative of a function or variable have been proposed by various mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation (and its opposite operation, the antidifferentiation or indefinite integration) are listed below. Leibniz's notation The original notation employed by Gottfried Leibniz is used throughout mathematics. It is particularly common when the equation is regarded as a functional relationship between dependent and independent variables and . Leibniz's notation makes this relationship explicit by writing the derivative as :\frac. Furthermore, the derivative of at is therefore written :\frac(x)\text\frac\text\frac f(x). Higher derivatives are written as :\frac, \frac, \frac, \ldots, \frac. This i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Calculus
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve. The primary objects of study in differential calculus are the derivative of a function, related notions such as the differential, and their applications. The derivative of a function at a chosen input value describes the rate of change of the function near that input value. The process of finding a derivative is called differentiation. Geometrically, the derivative at a point is the slope of the tangent line to the graph of the function at that point, provided that the derivative exists and is defined at that point. For a real-valued function of a single real variable, the derivative of a function at a point generally determines the best linear approximation to the function at that point. Differential calculus and integral calculus are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperreal Number
In mathematics, the system of hyperreal numbers is a way of treating infinite and infinitesimal (infinitely small but non-zero) quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form :1 + 1 + \cdots + 1 (for any finite number of terms). Such numbers are infinite, and their reciprocals are infinitesimals. The term "hyper-real" was introduced by Edwin Hewitt in 1948. The hyperreal numbers satisfy the transfer principle, a rigorous version of Leibniz's heuristic law of continuity. The transfer principle states that true first-order statements about R are also valid in *R. For example, the commutative law of addition, , holds for the hyperreals just as it does for the reals; since R is a real closed field, so is *R. Since \sin()=0 for all integers ''n'', one also has \sin()=0 for all hyperintegers H. The transfer principle for ultrapowers is a consequence of Łoś' theorem of 1955. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonstandard Analysis
The history of calculus is fraught with philosophical debates about the meaning and logical validity of fluxions or infinitesimal numbers. The standard way to resolve these debates is to define the operations of calculus using epsilon–delta procedures rather than infinitesimals. Nonstandard analysis instead reformulates the calculus using a logically rigorous notion of infinitesimal numbers. Nonstandard analysis originated in the early 1960s by the mathematician Abraham Robinson. He wrote: ... the idea of infinitely small or ''infinitesimal'' quantities seems to appeal naturally to our intuition. At any rate, the use of infinitesimals was widespread during the formative stages of the Differential and Integral Calculus. As for the objection ... that the distance between two distinct real numbers cannot be infinitely small, Gottfried Wilhelm Leibniz argued that the theory of infinitesimals implies the introduction of ideal numbers which might be infinitely small or infinitely ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Berkeley
George Berkeley (; 12 March 168514 January 1753) – known as Bishop Berkeley (Bishop of Cloyne of the Anglican Church of Ireland) – was an Anglo-Irish philosopher whose primary achievement was the advancement of a theory he called "immaterialism" (later referred to as " subjective idealism" by others). This theory denies the existence of material substance and instead contends that familiar objects like tables and chairs are ideas perceived by the mind and, as a result, cannot exist without being perceived. Berkeley is also known for his critique of abstraction, an important premise in his argument for immaterialism. In 1709, Berkeley published his first major work, '' An Essay Towards a New Theory of Vision'', in which he discussed the limitations of human vision and advanced the theory that the proper objects of sight are not material objects, but light and colour. This foreshadowed his chief philosophical work, ''A Treatise Concerning the Principles of Human Knowledg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |