|
Free Nutation
Nutation () is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behaviour of a mechanism. In an appropriate reference frame it can be defined as a change in the second Euler angle. If it is not caused by forces external to the body, it is called free nutation or Euler nutation (after Leonhard Euler). A pure nutation is a movement of a rotational axis such that the first Euler angle is constant. Therefore it can be seen that the circular red arrow in the diagram indicates the combined effects of precession and nutation, while nutation in the absence of precession would only change the tilt from vertical (second Euler angle). However, in spacecraft dynamics, precession (a change in the first Euler angle) is sometimes referred to as nutation. In a rigid body If a top is set at a tilt on a horizontal surface and spun rapidly, its rotational axis starts precessing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nutation
Nutation () is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behaviour of a mechanism. In an appropriate reference frame it can be defined as a change in the second Euler angle. If it is not caused by forces external to the body, it is called free nutation or Euler nutation (after Leonhard Euler). A pure nutation is a movement of a rotational axis such that the first Euler angle is constant. Therefore it can be seen that the circular red arrow in the diagram indicates the combined effects of precession and nutation, while nutation in the absence of precession would only change the tilt from vertical (second Euler angle). However, in spacecraft dynamics, precession (a change in the first Euler angle) is sometimes referred to as nutation. In a rigid body If a top is set at a tilt on a horizontal surface and spun rapidly, its rotational axis starts precess ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Potential
In classical mechanics, the gravitational potential is a scalar potential associating with each point in space the work (energy transferred) per unit mass that would be needed to move an object to that point from a fixed reference point in the conservative gravitational field. It is analogous to the electric potential with mass playing the role of charge. The reference point, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance. Their similarity is correlated with both associated fields having conservative forces. Mathematically, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies. Potential energy The gravitational potential (''V'') at a location is the gravitational potential ener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
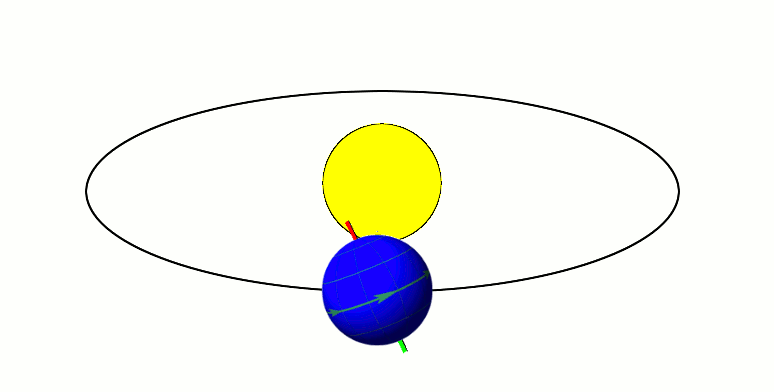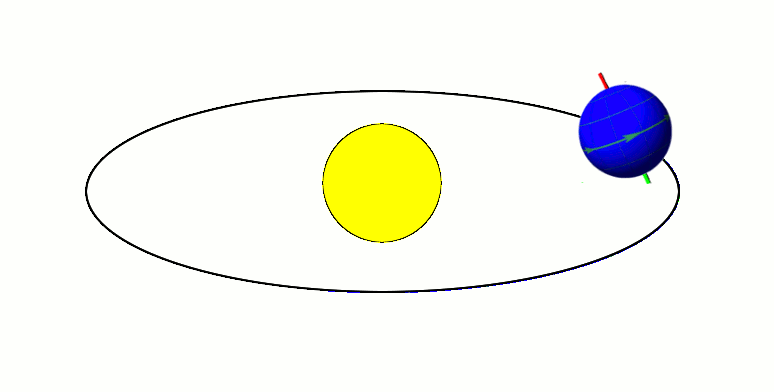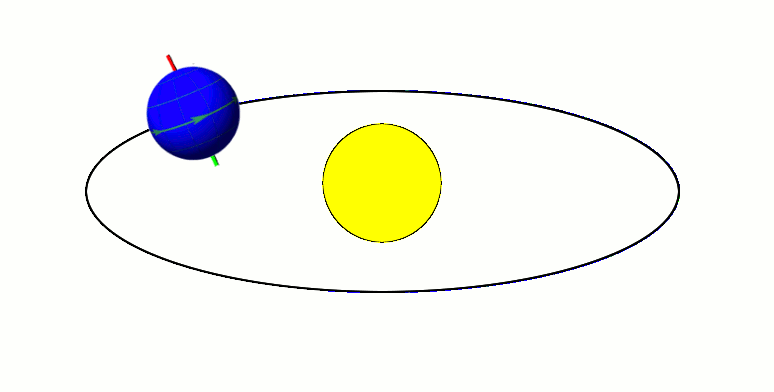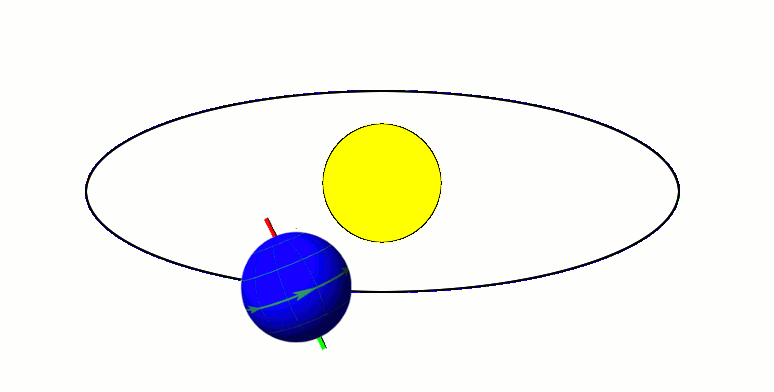
Axial Tilt
In astronomy, axial tilt, also known as obliquity, is the angle between an object's rotational axis and its orbital axis, which is the line perpendicular to its orbital plane; equivalently, it is the angle between its equatorial plane and orbital plane. It differs from orbital inclination. At an obliquity of 0 degrees, the two axes point in the same direction; that is, the rotational axis is perpendicular to the orbital plane. The rotational axis of Earth, for example, is the imaginary line that passes through both the North Pole and South Pole, whereas the Earth's orbital axis is the line perpendicular to the imaginary plane through which the Earth moves as it revolves around the Sun; the Earth's obliquity or axial tilt is the angle between these two lines. Over the course of an orbital period, the obliquity usually does not change considerably, and the orientation of the axis remains the same relative to the background of stars. This causes one pole to be pointed mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trópico De Cáncer En México - Carretera 83 (Vía Corta) Zaragoza-Victoria, Km 27+800
Trópico (Spanish and Portuguese for ‘tropic’) or Tropico may refer to: Computing * ''Tropico'' (series), a simulation, city-building video game franchise ** Tropico (video game), the first game in the series *Tropicos, an online botanical database Film and television * ''Tropico'' (2013 film), an American short film written by and starring Lana Del Rey * Tropico (upcoming film), an American film noir thriller * ''Trópico'' (TV series), a 2007 Venezuelan-Dominican telenovela Music * Davide Petrella, Italian singer-songwriter also known as Tropico * ''Tropico'' (Pat Benatar album), 1984 * ''Trópico'' (Ricardo Arjona album), 2009 *''Tropico'', an album by Gato Barbieri Leandro "Gato" Barbieri (November 28, 1932 – April 2, 2016) was an Argentine jazz tenor saxophonist who rose to fame during the free jazz movement in the 1960s and is known for his Latin jazz recordings of the 1970s. His nickname, Gato, is Spa ..., 1978 *''Tropico'', an album by Tony Esposito, 1996 Pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth's Rotation
Earth's rotation or Earth's spin is the rotation of planet Earth around its own Rotation around a fixed axis, axis, as well as changes in the orientation (geometry), orientation of the rotation axis in space. Earth rotates eastward, in prograde motion. As viewed from the northern polar star Polaris, Earth turns counterclockwise. The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where Earth's axis of rotation meets its surface. This point is distinct from Earth's north magnetic pole. The South Pole is the other point where Earth's axis of rotation intersects its surface, in Antarctica. Earth rotates once in about 24 hours with respect to the Sun, but once every 23 hours, 56 minutes and 4 seconds with respect to other distant stars (#Stellar and sidereal day, see below). Earth's rotation is slowing slightly with time; thus, a day was shorter in the past. This is due to the tidal acceleration, tidal effects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Bradley
James Bradley (September 1692 – 13 July 1762) was an English astronomer and priest who served as the third Astronomer Royal from 1742. He is best known for two fundamental discoveries in astronomy, the aberration of light (1725–1728), and the nutation of the Earth's axis (1728–1748). These two discoveries were called "the most brilliant and useful of the century" by Jean Baptiste Joseph Delambre, historian of astronomy, mathematical astronomer and director of the Paris Observatory. In his ''History of astronomy in the 18th century'' (1821), Delambre stated:"It is to these two discoveries by Bradley that we owe the exactness of modern astronomy. ... This double service assures to their discoverer the most distinguished place (after Hipparchus and Kepler) above the greatest astronomers of all ages and all countries." Biography Bradley was born at Sherborne, near Cheltenham in Gloucestershire, to William Bradley and Jane Pound in September 1692. His nephew John wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Precession
In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism. In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years.Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) ''Explanatory Supplement to the Astronomical Almanac''. Sausalito: University Science Books. p. 99. This is similar to the precession of a spinning top, with the axis tracing out a pair of cones joined at their apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis— nutation and polar motion—are much smaller in magnitude. Earth's precession was historically called the precession of the equinoxes, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t. Notation A variety of notations are used to denote the time derivative. In addition to the normal ( Leibniz's) notation, :\frac A very common short-hand notation used, especially in physics, is the 'over-dot'. I.E. :\dot (This is called Newton's notation) Higher time derivatives are also used: the second derivative with respect to time is written as :\frac with the corresponding shorthand of \ddot. As a generalization, the time derivative of a vector, say: : \mathbf v = \left v_1,\ v_2,\ v_3, \ldots \right is defined as the vector whose components are the derivatives of the components of the original vector. That is, : \frac = \left \frac,\frac ,\frac , \ldots \right . Use in physics Time derivatives are a key concept in physics. For example, for a changing position x, its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real number, real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as Series (mathematics), infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic function, periodic pheno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Function
In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d, that is, a polynomial function of degree three. In many texts, the ''coefficients'' , , , and are supposed to be real numbers, and the function is considered as a real function that maps real numbers to real numbers or as a complex function that maps complex numbers to complex numbers. In other cases, the coefficients may be complex numbers, and the function is a complex function that has the set of the complex numbers as its codomain, even when the domain is restricted to the real numbers. Setting produces a cubic equation of the form :ax^3+bx^2+cx+d=0, whose solutions are called roots of the function. The derivative of a cubic function is a quadratic function. A cubic function with real coefficients has either one or three real roots ( which may not be distinct); all odd-degree polynomials with real coefficients have at least one real root. The graph of a cubic function always has a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Of Motion
In mechanics, a constant of motion is a physical quantity conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a ''mathematical'' constraint, the natural consequence of the equations of motion, rather than a ''physical'' constraint (which would require extra constraint forces). Common examples include energy, linear momentum, angular momentum and the Laplace–Runge–Lenz vector (for inverse-square force laws). Applications Constants of motion are useful because they allow properties of the motion to be derived without solving the equations of motion. In fortunate cases, even the trajectory of the motion can be derived as the intersection of isosurfaces corresponding to the constants of motion. For example, Poinsot's construction shows that the torque-free rotation of a rigid body is the intersection of a sphere (conservation of total angular momentum) and an ellipsoid (conservation of energy), a trajectory that might be otherw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, ''Mécanique analytique''. Lagrangian mechanics describes a mechanical system as a pair consisting of a configuration space (physics), configuration space ''M'' and a smooth function L within that space called a ''Lagrangian''. For many systems, , where ''T'' and ''V'' are the Kinetic energy, kinetic and Potential energy, potential energy of the system, respectively. The stationary action principle requires that the Action (physics)#Action (functional), action functional of the system derived from ''L'' must remain at a stationary point (specifically, a Maximum and minimum, maximum, Maximum and minimum, minimum, or Saddle point, saddle point) throughout the time evoluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |