|
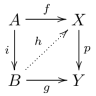
Factorization System
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory. Definition A factorization system (''E'', ''M'') for a category C consists of two classes of morphisms In mathematics, a morphism is a concept of category theory that generalizes structure-preserving maps such as homomorphism between algebraic structures, functions from a set to another set, and continuous functions between topological spaces. Al ... ''E'' and ''M'' of C such that: #''E'' and ''M'' both contain all isomorphisms of C and are closed under composition. #Every morphism ''f'' of C can be factored as f=m\circ e for some morphisms e\in E and m\in M. #The factorization is ''functorial'': if u and v are two morphisms such that vme=m'e'u for some morphisms e, e'\in E and m, m'\in M, then there exists a unique morphism w making the following diagram ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Comma Category
In mathematics, a comma category (a special case being a slice category) is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a Category (mathematics), category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by William Lawvere, F. W. Lawvere (Lawvere, 1963 p. 36), although the technique did not become generally known until many years later. Several mathematical concepts can be treated as comma categories. Comma categories also guarantee the existence of some Limit (category theory), limits and colimits. The name comes from the notation originally used by Lawvere, which involved the comma punctuation mark. The name persists even though standard notation has changed, since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category" (Lawvere, 1963 p. 13). Definition The most general comma ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Peter J
Peter may refer to: People * List of people named Peter, a list of people and fictional characters with the given name * Peter (given name) ** Saint Peter (died 60s), apostle of Jesus, leader of the early Christian Church * Peter (surname), a surname (including a list of people with the name) Culture * Peter (actor) (born 1952), stage name Shinnosuke Ikehata, a Japanese dancer and actor * ''Peter'' (1934 film), a film directed by Henry Koster * ''Peter'' (2021 film), a Marathi language film * "Peter" (''Fringe'' episode), an episode of the television series ''Fringe'' * ''Peter'' (novel), a 1908 book by Francis Hopkinson Smith * "Peter" (short story), an 1892 short story by Willa Cather * ''Peter'' (album), a 1972 album by Peter Yarrow * ''Peter'', a 1993 EP by Canadian band Eric's Trip * "Peter", 2024 song by Taylor Swift from '' The Tortured Poets Department: The Anthology'' Animals * Peter (Lord's cat), cat at Lord's Cricket Ground in London * Peter (chief mouse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Limit (category Theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as product (category theory), products, pullback (category theory), pullbacks and inverse limits. The duality (category theory), dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushout (category theory), pushouts and direct limits. Limits and colimits, like the strongly related notions of universal property, universal properties and adjoint functors, exist at a high level of abstraction. In order to understand them, it is helpful to first study the specific examples these concepts are meant to generalize. Definition Limits and colimits in a category (mathematics), category C are defined by means of diagrams in C. Formally, a diagram (category theory), diagram of shape J in C is a functor from J to C: :F:J\to C. The category J is thought of as an index category, and the diagram F is tho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Weak Equivalence (homotopy Theory)
In mathematics, a weak equivalence is a notion from homotopy theory that in some sense identifies objects that have the same "shape". This notion is formalized in the axiomatic definition of a model category. A model category is a category with classes of morphisms called weak equivalences, fibrations, and cofibrations, satisfying several axioms. The associated homotopy category of a model category has the same objects, but the morphisms are changed in order to make the weak equivalences into isomorphisms. It is a useful observation that the associated homotopy category depends only on the weak equivalences, not on the fibrations and cofibrations. Topological spaces Model categories were defined by Quillen as an axiomatization of homotopy theory that applies to topological spaces, but also to many other categories in algebra and geometry. The example that started the subject is the category of topological spaces with Serre fibrations as fibrations and weak homotopy equival ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Model Category
A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , . Models can be divided into physical models (e.g. a ship model or a fashion model) and abstract models (e.g. a set of mathematical equations describing the workings of the atmosphere for the purpose of weather forecasting). Abstract or conceptual models are central to philosophy of science. In scholarly research and applied science, a model should not be confused with a theory: while a model seeks only to represent reality with the purpose of better understanding or predicting the world, a theory is more ambitious in that it claims to be an explanation of reality. Types of model ''Model'' in specific contexts As a noun, ''model'' has specific meanings in certain fields, derived from its original meaning of "structural design or layout": * Model (art), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Right Lifting Property
In mathematics, in particular in category theory, the lifting property is a property of a pair of morphisms in a category. It is used in homotopy theory within algebraic topology to define properties of morphisms starting from an explicitly given class of morphisms. It appears in a prominent way in the theory of model categories, an axiomatic framework for homotopy theory introduced by Daniel Quillen. It is also used in the definition of a factorization system, and of a weak factorization system, notions related to but less restrictive than the notion of a model category. Several elementary notions may also be expressed using the lifting property starting from a list of (counter)examples. Formal definition A morphism i in a category has the ''left lifting property'' with respect to a morphism p, and p also has the ''right lifting property'' with respect to i, sometimes denoted i\perp p or i\downarrow p, iff the following implication holds for each morphism f and g in the category: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Factorization System Orthogonality
In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several '' factors'', usually smaller or simpler objects of the same kind. For example, is an ''integer factorization'' of , and is a ''polynomial factorization'' of . Factorization is not usually considered meaningful within number systems possessing division, such as the real or complex numbers, since any x can be trivially written as (xy)\times(1/y) whenever y is not zero. However, a meaningful factorization for a rational number or a rational function can be obtained by writing it in lowest terms and separately factoring its numerator and denominator. Factorization was first considered by ancient Greek mathematicians in the case of integers. They proved the fundamental theorem of arithmetic, which asserts that every positive integer may be factored into a product of prime numbers, which cannot be furth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Commutative Diagram
350px, The commutative diagram used in the proof of the five lemma In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra. Description A commutative diagram often consists of three parts: * objects (also known as ''vertices'') * morphisms (also known as ''arrows'' or ''edges'') * paths or composites Arrow symbols In algebra texts, the type of morphism can be denoted with different arrow usages: * A monomorphism may be labeled with a \hookrightarrow or a \rightarrowtail. * An epimorphism may be labeled with a \twoheadrightarrow. * An isomorphism may be labeled with a \overset. * The dashed arrow typically represents the claim that the indicated morphism exists (whenever the rest of the diagram holds); the arrow may be optionally labeled as \e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Isomorphisms
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is derived . The interest in isomorphisms lies in the fact that two isomorphic objects have the same properties (excluding further information such as additional structure or names of objects). Thus isomorphic structures cannot be distinguished from the point of view of structure only, and may often be identified. In mathematical jargon, one says that two objects are the same up to an isomorphism. A common example where isomorphic structures cannot be identified is when the structures are substructures of a larger one. For example, all subspaces of dimension one of a vector space are isomorphic and cannot be identified. An automorphism is an isomorphism from a structure to itself. An isomorphism between two structures is a cano ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |