|
F-divergence
In probability theory, an f-divergence is a certain type of function D_f(P\, Q) that measures the difference between two probability distributions P and Q. Many common divergences, such as KL-divergence, Hellinger distance, and total variation distance, are special cases of f-divergence. History These divergences were introduced by Alfréd Rényi in the same paper where he introduced the well-known Rényi entropy. He proved that these divergences decrease in Markov Process, Markov processes. ''f''-divergences were studied further independently by , and and are sometimes known as Csiszár f-divergences, Csiszár–Morimoto divergences, or Ali–Silvey distances. Definition Non-singular case Let P and Q be two probability distributions over a space \Omega, such that P\ll Q, that is, P is Absolute continuity#Absolute continuity of measures, absolutely continuous with respect to Q (meaning Q>0 wherever P>0). Then, for a convex function f: [0, +\infty)\to(-\infty, +\infty] ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Variation Distance
In probability theory, the total variation distance is a statistical distance between probability distributions, and is sometimes called the statistical distance, statistical difference or variational distance. Definition Consider a measurable space (\Omega, \mathcal) and probability measures P and Q defined on (\Omega, \mathcal). The total variation distance between P and Q is defined as :\delta(P,Q)=\sup_\left, P(A)-Q(A)\. This is the largest absolute difference between the probabilities that the two probability distributions assign to the same event. Properties The total variation distance is an F-divergence, ''f''-divergence and an integral probability metric. Relation to other distances The total variation distance is related to the Kullback–Leibler divergence by Pinsker's inequality, Pinsker’s inequality: :\delta(P,Q) \le \sqrt. One also has the following inequality, due to Bretagnolle–Huber inequality, Bretagnolle and Huber (see also ), which has the advantage ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hellinger Distance
In probability and statistics, the Hellinger distance (closely related to, although different from, the Bhattacharyya distance) is used to quantify the similarity between two probability distributions. It is a type of ''f''-divergence. The Hellinger distance is defined in terms of the Hellinger integral, which was introduced by Ernst Hellinger in 1909. It is sometimes called the Jeffreys distance. Definition Measure theory To define the Hellinger distance in terms of measure theory, let P and Q denote two probability measures on a measure space \mathcal that are absolutely continuous with respect to an auxiliary measure \lambda. Such a measure always exists, e.g \lambda = (P + Q). The square of the Hellinger distance between P and Q is defined as the quantity :H^2(P,Q) = \frac\displaystyle \int_ \left(\sqrt - \sqrt\right)^2 \lambda(dx). Here, P(dx) = p(x)\lambda(dx) and Q(dx) = q(x) \lambda(dx), i.e. p and q are the Radon–Nikodym derivatives of ''P'' and ''Q'' respect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
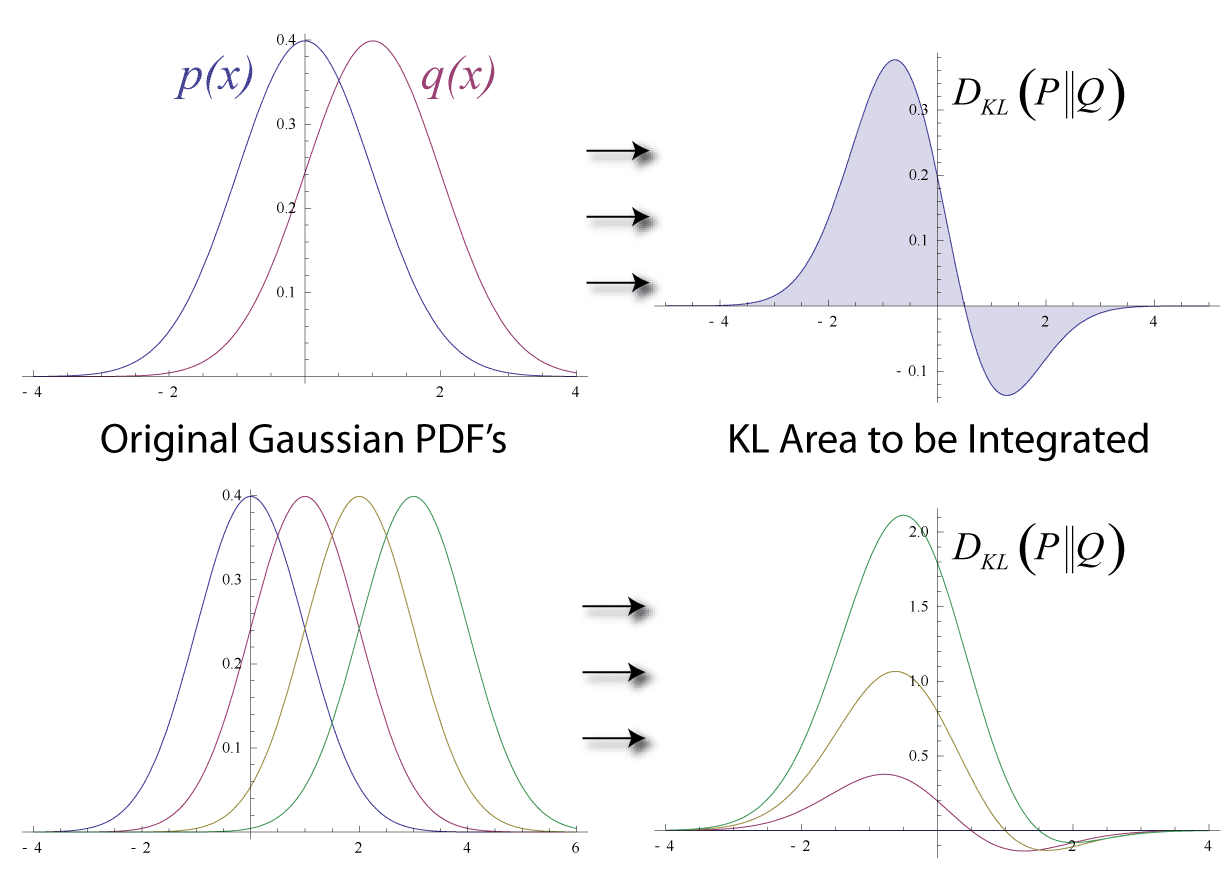
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Process
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). Markov processes are named in honor of the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes. They provide the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability distributions, and have found application in areas including Bayesian statistics, biology, chemistry, economics, finance, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jensen–Shannon Divergence
In probability theory and statistics, the Jensen–Shannon divergence, named after Johan Jensen and Claude Shannon, is a method of measuring the similarity between two probability distributions. It is also known as information radius (IRad) or total divergence to the average. It is based on the Kullback–Leibler divergence, with some notable (and useful) differences, including that it is symmetric and it always has a finite value. The square root of the Jensen–Shannon divergence is a metric often referred to as Jensen–Shannon distance. The similarity between the distributions is greater when the Jensen-Shannon distance is closer to zero. Definition Consider the set M_+^1(A) of probability distributions where A is a set provided with some σ-algebra of measurable subsets. In particular we can take A to be a finite or countable set with all subsets being measurable. The Jensen–Shannon divergence (JSD) is a symmetrized and smoothed version of the Kullback–Leibler divergen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cramér–Rao Bound
In estimation theory and statistics, the Cramér–Rao bound (CRB) relates to estimation of a deterministic (fixed, though unknown) parameter. The result is named in honor of Harald Cramér and Calyampudi Radhakrishna Rao, but has also been derived independently by Maurice Fréchet, Georges Darmois, and by Alexander Aitken and Harold Silverstone. It is also known as Fréchet-Cramér–Rao or Fréchet-Darmois-Cramér-Rao lower bound. It states that the precision of any unbiased estimator is at most the Fisher information; or (equivalently) the reciprocal of the Fisher information is a lower bound on its variance. An unbiased estimator that achieves this bound is said to be (fully) '' efficient''. Such a solution achieves the lowest possible mean squared error among all unbiased methods, and is, therefore, the minimum variance unbiased (MVU) estimator. However, in some cases, no unbiased technique exists which achieves the bound. This may occur either if for any unbiased ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Domain
In convex analysis, a branch of mathematics, the effective domain extends of the domain of a function defined for functions that take values in the extended real number line [-\infty, \infty] = \mathbb \cup \. In convex analysis and variational analysis, a point at which some given Extended real number line, extended real-valued function is minimized is typically sought, where such a point is called a global minimum point. The effective domain of this function is defined to be the set of all points in this function's domain at which its value is not equal to +\infty. It is defined this way because it is only these points that have even a remote chance of being a global minimum point. Indeed, it is common practice in these fields to set a function equal to +\infty at a point specifically to that point from even being considered as a potential solution (to the minimization problem). Points at which the function takes the value -\infty (if any) belong to the effective domain because s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Conjugate
In mathematics and mathematical optimization, the convex conjugate of a function is a generalization of the Legendre transformation which applies to non-convex functions. It is also known as Legendre–Fenchel transformation, Fenchel transformation, or Fenchel conjugate (after Adrien-Marie Legendre and Werner Fenchel). The convex conjugate is widely used for constructing the dual problem in optimization theory, thus generalizing Lagrangian duality. Definition Let X be a real topological vector space and let X^ be the dual space to X. Denote by :\langle \cdot , \cdot \rangle : X^ \times X \to \mathbb the canonical dual pairing, which is defined by \left\langle x^*, x \right\rangle \mapsto x^* (x). For a function f : X \to \mathbb \cup \ taking values on the extended real number line, its is the function :f^ : X^ \to \mathbb \cup \ whose value at x^* \in X^ is defined to be the supremum: :f^ \left( x^ \right) := \sup \left\, or, equivalently, in terms of the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |