|
Extension
Extension, extend or extended may refer to: Mathematics Logic or set theory * Axiom of extensionality * Extensible cardinal * Extension (model theory) * Extension (predicate logic), the set of tuples of values that satisfy the predicate * Extension (semantics), the set of things to which a property applies * Extension by definitions * Extensional definition, a definition that enumerates every individual a term applies to * Extensionality Other uses * Extension of a polyhedron, in geometry * Exterior algebra, Grassmann's theory of extension, in geometry * Homotopy extension property, in topology * Kolmogorov extension theorem, in probability theory * Linear extension, in order theory * Sheaf extension, in algebraic geometry * Tietze extension theorem, in topology * Whitney extension theorem, in differential geometry * Group extension, in abstract algebra and homological algebra Music * Extension (music), notes that fit outside the standard range * ''Extended'' (Solar Fiel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Extension
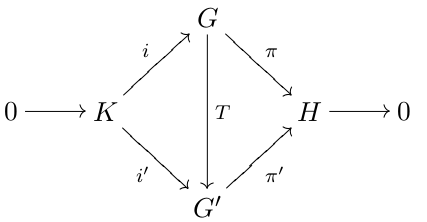
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Extension
In order theory, a branch of mathematics, a linear extension of a partial order is a total order (or linear order) that is compatible with the partial order. As a classic example, the lexicographic order of totally ordered sets is a linear extension of their product order. Definitions Given any partial orders \,\leq\, and \,\leq^*\, on a set X, \,\leq^*\, is a linear extension of \,\leq\, exactly when (1) \,\leq^*\, is a total order and (2) for every x, y \in X, if x \leq y, then x \leq^* y. It is that second property that leads mathematicians to describe \,\leq^*\, as extending \,\leq. Alternatively, a linear extension may be viewed as an order-preserving bijection from a partially ordered set P to a chain C on the same ground set. Order-extension principle The statement that every partial order can be extended to a total order is known as the order-extension principle. A proof using the axiom of choice was first published by Edward Marczewski in 1930. Marczewski ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extension (semantics)
In any of several fields of study that treat the use of signs — for example, in linguistics, logic, mathematics, semantics, semiotics, and philosophy of language — the extension of a concept, idea, or sign consists of the things to which it applies, in contrast with its comprehension or intension, which consists very roughly of the ideas, properties, or corresponding signs that are implied or suggested by the concept in question. In philosophical semantics or the philosophy of language, the 'extension' of a concept or expression is the set of things it extends to, or applies to, if it is the sort of concept or expression that a single object by itself can satisfy. Concepts and expressions of this sort are monadic or "one-place" concepts and expressions. So the extension of the word "dog" is the set of all (past, present and future) dogs in the world: the set includes Fido, Rover, Lassie, Rex, and so on. The extension of the phrase "Wikipedia reader" includes each pers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
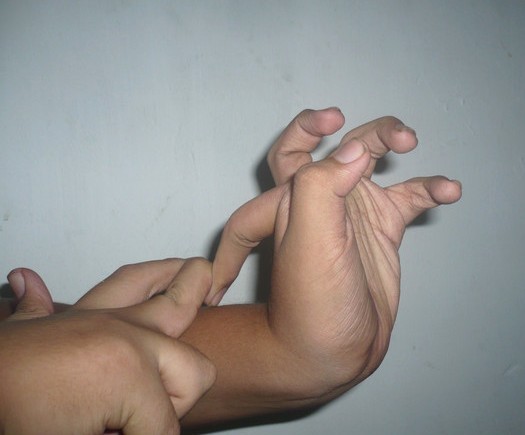
Extension (anatomy)
Motion, the process of movement, is described using specific anatomical terms. Motion includes movement of organs, joints, limbs, and specific sections of the body. The terminology used describes this motion according to its direction relative to the anatomical position of the body parts involved. Anatomists and others use a unified set of terms to describe most of the movements, although other, more specialized terms are necessary for describing unique movements such as those of the hands, feet, and eyes. In general, motion is classified according to the anatomical plane it occurs in. ''Flexion'' and ''extension'' are examples of ''angular'' motions, in which two axes of a joint are brought closer together or moved further apart. ''Rotational'' motion may occur at other joints, for example the shoulder, and are described as ''internal'' or ''external''. Other terms, such as ''elevation'' and ''depression'', describe movement above or below the horizontal plane. Many anatom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extensions (The Manhattan Transfer Album)
Extension, extend or extended may refer to: Mathematics Logic or set theory * Axiom of extensionality * Extensible cardinal * Extension (model theory) * Extension (predicate logic), the set of tuples of values that satisfy the predicate * Extension (semantics), the set of things to which a property applies * Extension by definitions * Extensional definition, a definition that enumerates every individual a term applies to * Extensionality Other uses * Extension of a polyhedron, in geometry * Exterior algebra, Grassmann's theory of extension, in geometry * Homotopy extension property, in topology * Kolmogorov extension theorem, in probability theory * Linear extension, in order theory * Sheaf extension, in algebraic geometry * Tietze extension theorem, in topology * Whitney extension theorem, in differential geometry * Group extension, in abstract algebra and homological algebra Music * Extension (music), notes that fit outside the standard range * ''Extended'' (Solar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extension (geology)
Extensional tectonics is concerned with the structures formed by, and the tectonic processes associated with, the stretching of a planetary body's crust or lithosphere. Deformation styles The types of structure and the geometries formed depend on the amount of stretching involved. Stretching is generally measured using the parameter ''β'', known as the ''beta factor'', where : \beta = \frac \,, ''t''0 is the initial crustal thickness and ''t''1 is the final crustal thickness. It is also the equivalent of the strain parameter ''stretch''. Low beta factor In areas of relatively low crustal stretching, the dominant structures are high to moderate angle normal faults, with associated half grabens and tilted fault blocks. High beta factor In areas of high crustal stretching, individual extensional faults may become rotated to too low a dip to remain active and a new set of faults may be generated. Large displacements may juxtapose syntectonic sediments against metamorphic r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extension (music)
In music, an extension is a set of musical notes that lie outside the standard range or tessitura. Staff A note that lies outside the lines of a musical staff is an extension of the staff. The note will lie on a ledger line. Middle C, for example, is an extension note on both treble and bass clefs, however is not outside the grand staff. Soprano C and Deep C lie two ledger lines above treble and below bass respectively (as well as the grand staff). Instruments An instrumental extension is a range of playable notes outside the normal range of the instrument. A baritone horn, if played by a skillful player, can be played an octave above the normal range. Since this is not standard, these notes would be an extension. (See also: Crook (music)). With the bowed string instruments, lower pitches than the standard range are sometimes used through scordatura in which the lowest string is tuned down a note or two. The double bass sometimes uses a C extension extending the ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extensionality
In logic, extensionality, or extensional equality, refers to principles that judge objects to be equal if they have the same external properties. It stands in contrast to the concept of intensionality, which is concerned with whether the internal definitions of objects are the same. Example Consider the two functions ''f'' and ''g'' mapping from and to natural numbers, defined as follows: * To find ''f''(''n''), first add 5 to ''n'', then multiply by 2. * To find ''g''(''n''), first multiply ''n'' by 2, then add 10. These functions are extensionally equal; given the same input, both functions always produce the same value. But the definitions of the functions are not equal, and in that intensional sense the functions are not the same. Similarly, in natural language there are many predicates (relations) that are intensionally different but are extensionally identical. For example, suppose that a town has one person named Joe, who is also the oldest person in the town. Then, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Extension Property
In mathematics, in the area of algebraic topology, the homotopy extension property indicates which homotopies defined on a subspace can be extended to a homotopy defined on a larger space. The homotopy extension property of cofibrations is dual to the homotopy lifting property that is used to define fibrations. Definition Let X\,\! be a topological space, and let A \subset X. We say that the pair (X,A)\,\! has the homotopy extension property if, given a homotopy f_t\colon A \rightarrow Y and a map \tilde_0\colon X \rightarrow Y such that \left.\tilde_0\_A = f_0, there exists an ''extension'' of f_t to a homotopy \tilde_t\colon X \rightarrow Y such that \left.\tilde_t\_A = f_t.A. Dold, ''Lectures on Algebraic Topology'', pp. 84, Springer That is, the pair (X,A)\,\! has the homotopy extension property if any map G\colon ((X\times \) \cup (A\times I)) \rightarrow Y can be extended to a map G'\colon X\times I \rightarrow Y (i.e. G\,\! and G'\,\! agree on their common domain). If ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extension By Definitions
In mathematical logic, more specifically in the proof theory of first-order theories, extensions by definitions formalize the introduction of new symbols by means of a definition. For example, it is common in naive set theory to introduce a symbol \emptyset for the set which has no member. In the formal setting of first-order theories, this can be done by adding to the theory a new constant \emptyset and the new axiom \forall x(x\notin\emptyset), meaning "for all ''x'', ''x'' is not a member of \emptyset". It can then be proved that doing so adds essentially nothing to the old theory, as should be expected from a definition. More precisely, the new theory is a conservative extension of the old one. Definition of relation symbols ''Let'' T be a first-order theory and \phi(x_1,\dots,x_n) a formula of T such that x_1, ..., x_n are distinct and include the variables free in \phi(x_1,\dots,x_n). Form a new first-order theory T' from T by adding a new n-ary relation symbol R, the lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extension Of A Polyhedron
In convex geometry and polyhedral combinatorics, the extension complexity is a convex polytope P is the smallest number of facets among convex polytopes Q that have P as a projection. In this context, Q is called an extended formulation of P; it may have much higher dimension than P. The extension complexity depends on the precise shape of P, not just on its combinatorial structure. For instance, regular polygons with n sides have extension complexity O(\log n) (expressed using big O notation), but some other convex n-gons have extension complexity at least proportional to \sqrt. If a polytope describing the feasible solutions to a combinatorial optimization problem has low extension complexity, this could potentially be used to devise efficient algorithms for the problem, using linear programming on its extended formulation. For this reason, researchers have studied the extension complexity of the polytopes arising in this way. For instance, it is known that the matching polyto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |