|
Exsecant
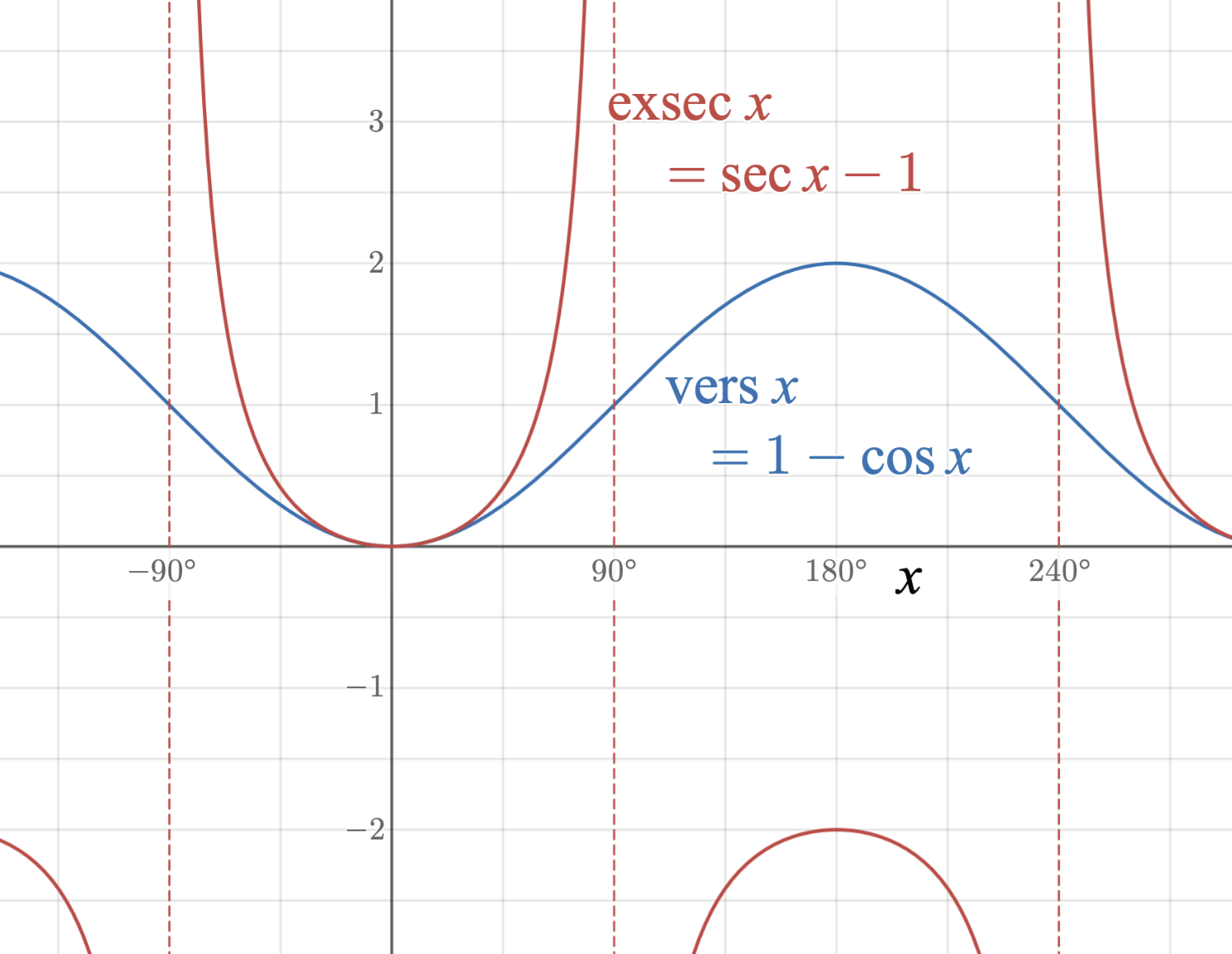
The external secant function (abbreviated exsecant, symbolized exsec) is a trigonometric function defined in terms of the secant function: \operatorname \theta = \sec\theta - 1 = \frac - 1. It was introduced in 1855 by American civil engineer Charles Haslett, who used it in conjunction with the existing versine function, \operatorname\theta = 1 - \cos\theta, for designing and measuring circular sections of railroad track. It was adopted by surveyors and civil engineers in the United States for railroad and road design, and since the early 20th century has sometimes been briefly mentioned in American trigonometry textbooks and general-purpose engineering manuals. For completeness, a few books also defined a coexsecant or excosecant function (symbolized coexsec or excsc), \operatorname \theta = \csc\theta - 1, the exsecant of the complementary angle, though it was not used in practice. While the exsecant has occasionally found other applications, today it is obscure and main ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exsecant And Versine
The external secant function (abbreviated exsecant, symbolized exsec) is a trigonometric function defined in terms of the secant (trigonometry), secant function: \operatorname \theta = \sec\theta - 1 = \frac - 1. It was introduced in 1855 by American civil engineering, civil engineer Charles Haslett, who used it in conjunction with the existing versine function, \operatorname\theta = 1 - \cos\theta, for designing and measuring circular arc, circular sections of railroad track. It was adopted by surveying, surveyors and civil engineers in the United States for railroad and geometric design of roads, road design, and since the early 20th century has sometimes been briefly mentioned in American trigonometry textbooks and general-purpose engineering manuals. For completeness, a few books also defined a coexsecant or excosecant function (symbolized coexsec or excsc), \operatorname \theta = \csc\theta - 1, the exsecant of the complementary angle, though it was not used in practice. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Design Of Roads
The geometric design of roads is the branch of highway engineering concerned with the positioning of the physical elements of the roadway according to standards and constraints. The basic objectives in geometric design are to optimize efficiency and safety while minimizing cost and environmental damage. Geometric design also affects an emerging fifth objective called "livability", which is defined as designing roads to foster broader community goals, including providing access to employment, schools, businesses and residences, accommodate a range of travel modes such as walking, bicycling, transit, and automobiles, and minimizing fuel use, emissions and environmental damage. Geometric roadway design can be broken into three main parts: alignment, profile, and cross-section. Combined, they provide a three-dimensional layout for a roadway. * The alignment is the route of the road, defined as a series of horizontal tangents and curves. * The profile is the vertical aspect of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their multiplicative inverse, reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding Inverse trigonometric functions, inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secant (trigonometry)
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secant Function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To exte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Fincke
Thomas Fincke (6 January 1561 – 24 April 1656) was a Danish mathematician and physicist, and a professor at the University of Copenhagen for more than 60 years. Biography Thomas Jacobsen Fincke was born in Flensburg in Schleswig. Fincke was the son of Councillor Jacob Fincke and Anna Thorsmede. He completed his primary schooling at Flensburg. From 1577, he studied mathematics, rhetoric and other philosophical studies for five years at the University of Strasbourg. Fincke's lasting achievement is found in his book ''Geometria rotundi'' (1583), in which he introduced the modern names of the trigonometric functions tangent and secant. In 1590, he became professor of mathematics at the University of Copenhagen. In 1603 he also obtained a professorship in medicine. Personal life He was married to Ivaria Jungesdatter Ivers (1574–1614). His son Jacob Fincke (1592–1663) was a professor of physics. His daughters married scientist Caspar Bartholin the Elder (1585–1629), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a polymath. He was born in the city of Pisa, then part of the Duchy of Florence. Galileo has been called the father of observational astronomy, modern-era classical physics, the scientific method, and modern science. Galileo studied speed and velocity, gravity and free fall, the principle of relativity, inertia, projectile motion and also worked in applied science and technology, describing the properties of the pendulum and "hydrostatic balances". He was one of the earliest Renaissance developers of the thermoscope and the inventor of various sector (instrument), military compasses. With an improved telescope he built, he observed the stars of the Milky Way, the phases of Venus, the Galilean moons, four largest satellites of Jupiter, Saturn's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surveying
Surveying or land surveying is the technique, profession, art, and science of determining the land, terrestrial Plane (mathematics), two-dimensional or Three-dimensional space#In Euclidean geometry, three-dimensional positions of Point (geometry), points and the Euclidean distance, distances and angles between them. These points are usually on the surface of the Earth, and they are often used to establish maps and boundaries for ownership, locations, such as the designated positions of structural components for construction or the surface location of subsurface features, or other purposes required by government or civil law, such as property sales. A professional in land surveying is called a land surveyor. Surveyors work with elements of geodesy, geometry, trigonometry, regression analysis, physics, engineering, metrology, programming languages, and the law. They use equipment, such as total stations, robotic total stations, theodolites, Satellite navigation, GNSS receivers, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Common Logarithm
In mathematics, the common logarithm (aka "standard logarithm") is the logarithm with base 10. It is also known as the decadic logarithm, the decimal logarithm and the Briggsian logarithm. The name "Briggsian logarithm" is in honor of the British mathematician Henry Briggs who conceived of and developed the values for the "common logarithm". Historically', the "common logarithm" was known by its Latin name ''logarithmus decimalis'' or ''logarithmus decadis''. The mathematical notation for using the common logarithm is , , or sometimes with a capital ; on calculators, it is printed as "log", but mathematicians usually mean natural logarithm (logarithm with base ≈ 2.71828) rather than common logarithm when writing "log". Before the early 1970s, handheld electronic calculators were not available, and mechanical calculators capable of multiplication were bulky, expensive and not widely available. Instead, tables of base-10 logarithms were used in science, engineering and navi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (geometry)
A chord (from the Latin ''chorda'', meaning " bowstring") of a circle is a straight line segment whose endpoints both lie on a circular arc. If a chord were to be extended infinitely on both directions into a line, the object is a ''secant line''. The perpendicular line passing through the chord's midpoint is called '' sagitta'' (Latin for "arrow"). More generally, a chord is a line segment joining two points on any curve, for instance, on an ellipse. A chord that passes through a circle's center point is the circle's ''diameter''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Angle
A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B. Central angles are subtended by an arc between those two points, and the arc length is the central angle of a circle of radius one (measured in radians). The central angle is also known as the arc's angular distance. The arc length spanned by a central angle on a sphere is called '' spherical distance''. The size of a central angle is or (radians). When defining or drawing a central angle, in addition to specifying the points and , one must specify whether the angle being defined is the convex angle (<180°) or the reflex angle (>180°). Equivalently, one must specify whether the movement from point to point is clockwise or counterclockwise. Formulas If the intersection points and of the legs of the angle with the circle form a diameter, then is a straight angle. (In radians, .) Let be the min ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersecting Secants Theorem
In Euclidean geometry, the intersecting secants theorem or just secant theorem describes the relation of line segments created by two intersecting secants and the associated circle. For two lines and that intersect each other at and for which all lie on the same circle, the following equation holds: , PA, \cdot, PD, = , PB, \cdot, PC, The theorem follows directly from the fact that the triangles and are similar. They share and as they are inscribed angles over . The similarity yields an equation for ratios which is equivalent to the equation of the theorem given above: \frac=\frac \Leftrightarrow , PA, \cdot, PD, =, PB, \cdot, PC, Next to the intersecting chords theorem In Euclidean geometry, the intersecting chords theorem, or just the chord theorem, is a statement that describes a relation of the four line segments created by two intersecting chords within a circle. It states that the products of the lengt ... and the tangent-secant theorem, the intersec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |