|
Digital Filters
In signal processing, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is typically an electronic circuit operating on continuous-time analog signals. A digital filter system usually consists of an analog-to-digital converter (ADC) to sample the input signal, followed by a microprocessor and some peripheral components such as memory to store data and filter coefficients etc. Program Instructions (software) running on the microprocessor implement the digital filter by performing the necessary mathematical operations on the numbers received from the ADC. In some high performance applications, an FPGA or ASIC is used instead of a general purpose microprocessor, or a specialized digital signal processor (DSP) with specific paralleled architecture for expediting operations such as f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FIR Filter General
Firs (''Abies'') are a genus of 48–56 species of evergreen coniferous trees in the family Pinaceae. They are found on mountains throughout much of North and Central America, Europe, Asia, and North Africa. The genus is most closely related to ''Cedrus'' (cedar). The genus name is derived from the Latin "to rise" in reference to the height of its species. The common English name originates with the Old Norse, fyri, or the Old Danish, fyr. They are large trees, reaching heights of tall with trunk diameters of when mature. Firs can be distinguished from other members of the pine family by the way in which their needle-like leaves are attached singly to the branches with a base resembling a suction cup, and by their cones, which, like those of true cedars, stand upright on the branches like candles and disintegrate at maturity. Identification of the different species is based on the size and arrangement of the leaves, the size and shape of the cones, and whether the bract s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
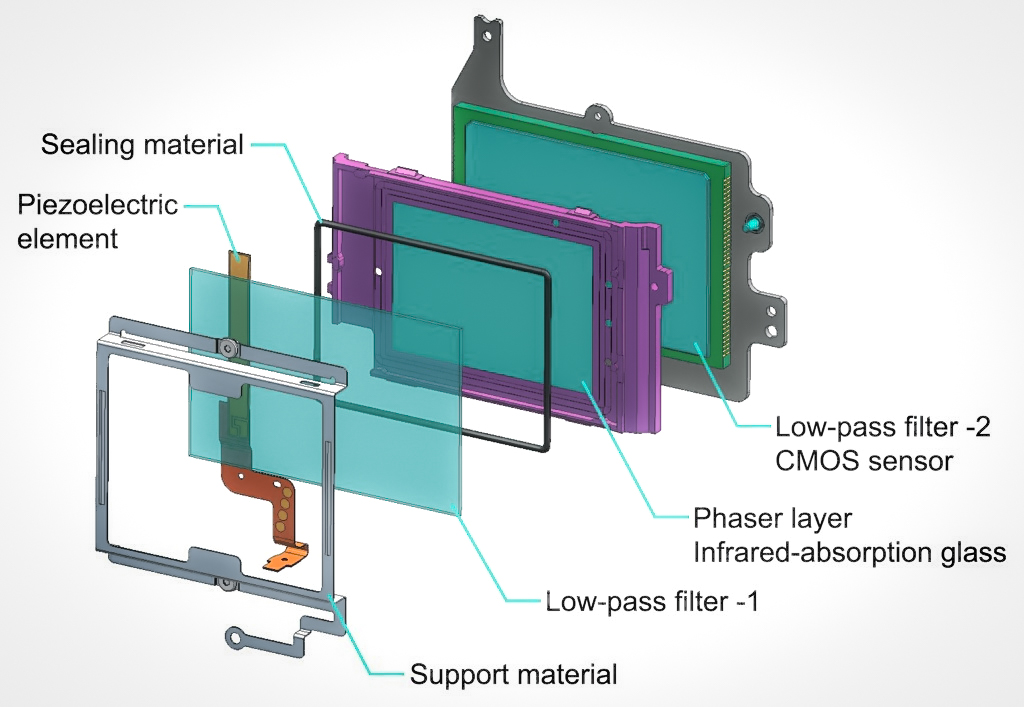
Anti-aliasing Filter
An anti-aliasing filter (AAF) is a filter used before a signal sampler to restrict the bandwidth of a signal to satisfy the Nyquist–Shannon sampling theorem over the band of interest. Since the theorem states that unambiguous reconstruction of the signal from its samples is possible when the power of frequencies above the Nyquist frequency is zero, a brick wall filter is an idealized but impractical AAF. A practical AAF makes a trade off between reduced bandwidth and increased aliasing. A practical anti-aliasing filter will typically permit some aliasing to occur or attenuate or otherwise distort some in-band frequencies close to the Nyquist limit. For this reason, many practical systems sample higher than would be theoretically required by a perfect AAF in order to ensure that all frequencies of interest can be reconstructed, a practice called oversampling. Optical applications The Pentax K-3 from Ricoh introduced a unique sensor-based anti-aliasing filter. The fil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise: \delta_ = \begin 0 &\text i \neq j, \\ 1 &\text i=j. \end or with use of Iverson brackets: \delta_ = =j, where the Kronecker delta is a piecewise function of variables and . For example, , whereas . The Kronecker delta appears naturally in many areas of mathematics, physics and engineering, as a means of compactly expressing its definition above. In linear algebra, the identity matrix has entries equal to the Kronecker delta: I_ = \delta_ where and take the values , and the inner product of vectors can be written as \mathbf\cdot\mathbf = \sum_^n a_\delta_b_ = \sum_^n a_ b_. Here the Euclidean vectors are defined as -tuples: \mathbf = (a_1, a_2, \dots, a_n) and \mathbf= (b_1, b_2, ..., b_n) and the last step is obtained by using the values of the Kronecker del ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Impulse Response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time (or possibly as a function of some other independent variable that parameterizes the dynamic behavior of the system). In all these cases, the dynamic system and its impulse response may be actual physical objects, or may be mathematical systems of equations describing such objects. Since the impulse function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function has), the impulse response defines the response of a linear time-invariant system for all frequencies. Mathematical consideratio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
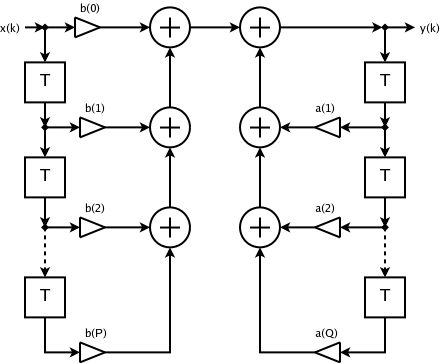
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the output s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1 (number)
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Denominator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A ''common'', ''vulgar'', or ''simple'' fraction (examples: \tfrac and \tfrac) consists of a numerator, displayed above a line (or before a slash like ), and a non-zero denominator, displayed below (or after) that line. Numerators and denominators are also used in fractions that are not ''common'', including compound fractions, complex fractions, and mixed numerals. In positive common fractions, the numerator and denominator are natural numbers. The numerator represents a number of equal parts, and the denominator indicates how many of those parts make up a unit or a whole. The denominator cannot be zero, because zero parts can never make up a whole. For example, in the fraction , the numerator 3 indicates that the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) which does not become exactly zero past a certain point, but continues indefinitely. This is in contrast to a finite impulse response (FIR) system in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive Filter
In signal processing, a recursive filter is a type of filter which re-uses one or more of its outputs as an input. This feedback typically results in an unending impulse response (commonly referred to as ''infinite impulse response'' (IIR)), characterised by either exponentially growing, decaying, or sinusoid A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in ...al signal output components. However, a recursive filter does not always have an infinite impulse response. Some implementations of moving average filter are recursive filters but with a finite impulse response. Non-recursive Filter Example: y = 0.5x − 1+ 0.5x Recursive Filter Example: y = 0.5y − 1+ 0.5x Examples of recursive filters * Kalman filter Signal processing {{signal-processing-stub Weblinks IIR F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain (z-domain or z-plane) representation. It can be considered as a discrete-time equivalent of the Laplace transform (s-domain). This similarity is explored in the theory of time-scale calculus. Whereas the continuous-time Fourier transform is evaluated on the Laplace s-domain's imaginary line, the discrete-time Fourier transform is evaluated over the unit circle of the z-domain. What is roughly the s-domain's left half-plane, is now the inside of the complex unit circle; what is the z-domain's outside of the unit circle, roughly corresponds to the right half-plane of the s-domain. One of the means of designing digital filters is to take analog designs, subject them to a bilinear transform which maps them from the s-domain to the z-domain, and then produce the digital filter by inspection, manipulation, or numeric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Equation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer Function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a mathematical function that theoretically models the system's output for each possible input. They are widely used in electronics and control systems. In some simple cases, this function is a two-dimensional graph of an independent scalar input versus the dependent scalar output, called a transfer curve or characteristic curve. Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory. The dimensions and units of the transfer function model the output response of the device for a range of possible inputs. For example, the transfer function of a two-port electronic circuit like an amplifier might be a two-dimensional graph of the scalar voltage at the output as a function of the scalar voltage applied to the input; the tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |