|
Degenerate Conic
In geometry, a degenerate conic is a conic (a second-degree plane curve, defined by a polynomial equation of degree two) that fails to be an irreducible variety, irreducible curve. This means that the defining equation is factorable over the complex numbers (or more generally over an algebraically closed field) as the product of two linear polynomials.Some authors consider conics without real points as degenerate, but this is not a commonly accepted convention. Using the alternative definition of the conic as the intersection in three-dimensional space of a plane (geometry), plane and a double cone (geometry), cone, a conic is degenerate if the plane goes through the vertex of the cones. In the real plane, a degenerate conic can be two lines that may or may not be parallel, a single line (either two coinciding lines or the union of a line and the line at infinity), a single point (in fact, two complex conjugate lines), or the null set (twice the line at infinity or two parallel c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apollonian Circles
In geometry, Apollonian circles are two families (pencils) of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. They were discovered by Apollonius of Perga, a renowned Greek geometer. Definition The Apollonian circles are defined in two different ways by a line segment denoted ''CD''. Each circle in the first family (the blue circles in the figure) is associated with a positive real number ''r'', and is defined as the locus of points ''X'' such that the ratio of distances from ''X'' to ''C'' and to ''D'' equals ''r'', :\left\. For values of ''r'' close to zero, the corresponding circle is close to ''C'', while for values of ''r'' close to ∞, the corresponding circle is close to ''D''; for the intermediate value ''r'' = 1, the circle degenerates to a line, the perpendicular bisector of ''CD''. The equation defining these circles as a locus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compactification (mathematics)
In mathematics, in general topology, compactification is the process or result of making a topological space into a compact space. A compact space is a space in which every open cover of the space contains a finite subcover. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape". An example Consider the real line with its ordinary topology. This space is not compact; in a sense, points can go off to infinity to the left or to the right. It is possible to turn the real line into a compact space by adding a single "point at infinity" which we will denote by ∞. The resulting compactification can be thought of as a circle (which is compact as a closed and bounded subset of the Euclidean plane). Every sequence that ran off to infinity in the real line will then converge to ∞ in this compactification. Intuitively, the process can be pictured as follow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Varieties
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition. Conventions regarding the definition of an algebraic variety differ slightly. For example, some definitions require an algebraic variety to be irreducible, which means that it is not the union of two smaller sets that are closed in the Zariski topology. Under this definition, non-irreducible algebraic varieties are called algebraic sets. Other conventions do not require irreducibility. The fundamental theorem of algebra establishes a link between algebra and geometry by showing that a monic polynomial (an algebraic object) in one variable with complex number coefficients is determine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
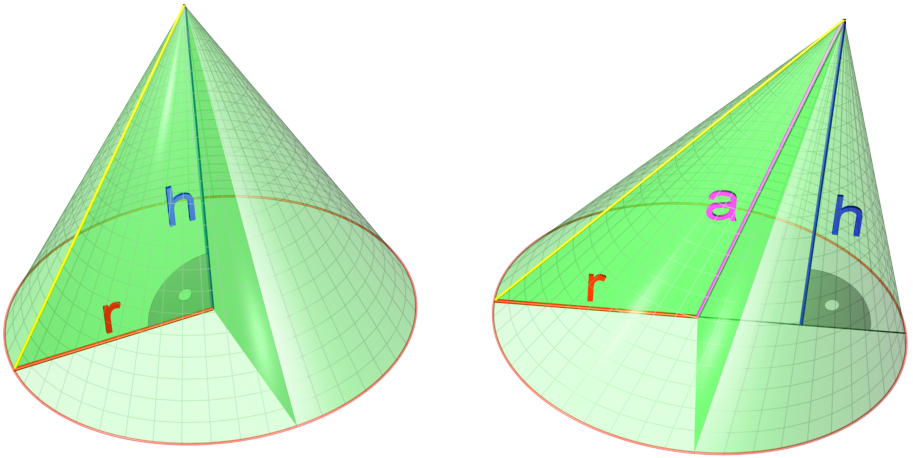
Apex (geometry)
In geometry, an apex (plural apices) is the vertex which is in some sense the "highest" of the figure to which it belongs. The term is typically used to refer to the vertex opposite from some " base". The word is derived from the Latin for 'summit, peak, tip, top, extreme end'. Isosceles triangles In an isosceles triangle, the apex is the vertex where the two sides of equal length meet, opposite the unequal third side. Pyramids and cones In a pyramid or cone A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines con ..., the apex is the vertex at the "top" (opposite the base). In a pyramid, the vertex is the point that is part of all the lateral faces, or where all the lateral edges meet. References {{elementary-geometry-stub Parts of a triangle Polyhedra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cone
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a specia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry. The discriminant of the quadratic polynomial ax^2+bx+c is :b^2-4ac, the quantity which appears under the square root in the quadratic formula. If a\ne 0, this discriminant is zero if and only if the polynomial has a double root. In the case of real coefficients, it is positive if the polynomial has two distinct real roots, and negative if it has two distinct complex conjugate roots. Similarly, the discriminant of a cubic polynomial is zero if and only if the polynomial has a multiple root. In the case of a cubic with real coefficients, the discriminant is positive if the polynomial has three distinct real roots, and negat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Lines
In geometry, parallel lines are coplanar straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. ''Parallel curves'' are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called '' skew lines''. Parallel lines are the subject of Euclid's parallel postulate. Parallelism is primarily a property of affine geometries and Euclidean geometry is a special instance of this type of geometry. In some other geometries, such as hyperbolic geometry, lines can have analogous properties that are referred to as parallelism. Symbol The parallel symbol is \parallel. For example, AB \parallel CD indicates that line ''AB'' is parallel to line ''CD''. In the Unicode character set, the "parallel" and "not parallel" signs have code ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersecting Lines
In geometry, an intersection is a point, line, or curve common to two or more objects (such as lines, curves, planes, and surfaces). The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point or does not exist (if the lines are parallel). Other types of geometric intersection include: * Line–plane intersection * Line–sphere intersection * Intersection of a polyhedron with a line * Line segment intersection * Intersection curve Determination of the intersection of flats – linear geometric objects embedded in a higher-dimensional space – is a simple task of linear algebra, namely the solution of a system of linear equations. In general the determination of an intersection leads to non-linear equations, which can be solved numerically, for example using Newton iteration. Intersection problems between a line and a conic section (circle, ellipse, parabola, etc.) or a quadric (sphere, cylinder, hyperboloid, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. If is the point set of an affine space, then every affine transformation on can b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)
