|
Distance Matrix
In mathematics, computer science and especially graph theory, a distance matrix is a square matrix (two-dimensional array) containing the distances, taken pairwise, between the elements of a set. Depending upon the application involved, the ''distance'' being used to define this matrix may or may not be a metric (mathematics), metric. If there are elements, this matrix will have size . In graph-theoretic applications, the elements are more often referred to as points, nodes or vertices. Non-metric distance matrix In general, a distance matrix is a weighted adjacency matrix of some graph. In a Network (mathematics), network, a directed graph with weights assigned to the arcs, the distance between two nodes of the network can be defined as the minimum of the sums of the weights on the shortest paths joining the two nodes (where the number of steps in the path is bounded). This distance function, while well defined, is not a metric. There need be no restrictions on the weights oth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hollow Matrix
In mathematics, a hollow matrix may refer to one of several related classes of matrix: a sparse matrix; a matrix with a large block of zeroes; or a matrix with diagonal entries all zero. Definitions Sparse A ''hollow matrix'' may be one with "few" non-zero entries: that is, a sparse matrix. Block of zeroes A ''hollow matrix'' may be a square matrix with an block of zeroes where . Diagonal entries all zero A ''hollow matrix'' may be a square matrix whose diagonal elements are all equal to zero. That is, an matrix is hollow if whenever (i.e. for all ). The most obvious example is the real skew-symmetric matrix. Other examples are the adjacency matrix of a finite simple graph, and a distance matrix or Euclidean distance matrix. In other words, any square matrix that takes the form \begin 0 & \ast & & \ast & \ast \\ \ast & 0 & & \ast & \ast \\ & & \ddots \\ \ast & \ast & & 0 & \ast \\ \ast & \ast & & \ast & 0 \end is a hollow matrix, where the symbol \a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
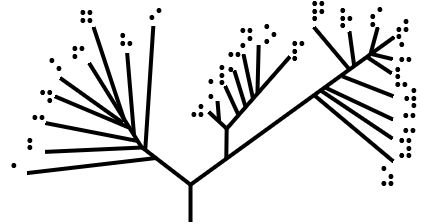
Ultrametric Tree
In mathematics, an ultrametric space is a metric space in which the triangle inequality is strengthened to d(x,z)\leq\max\left\ for all x, y, and z. Sometimes the associated metric is also called a non-Archimedean metric or super-metric. Formal definition An ultrametric on a set is a real-valued function :d\colon M \times M \rightarrow \mathbb (where denote the real numbers), such that for all : # ; # (''symmetry''); # ; # if then ; # (strong triangle inequality or ultrametric inequality). An ultrametric space is a pair consisting of a set together with an ultrametric on , which is called the space's associated distance function (also called a metric). If satisfies all of the conditions except possibly condition 4, then is called an ultrapseudometric on . An ultrapseudometric space is a pair consisting of a set and an ultrapseudometric on . In the case when is an Abelian group (written additively) and is generated by a length function \, \cdot\, (so that d(x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Clock
The molecular clock is a figurative term for a technique that uses the mutation rate of biomolecules to deduce the time in prehistory when two or more life forms diverged. The biomolecular data used for such calculations are usually nucleotide sequences for DNA, RNA, or amino acid sequences for proteins. Early discovery and genetic equidistance The notion of the existence of a so-called "molecular clock" was first attributed to Émile Zuckerkandl and Linus Pauling who, in 1962, noticed that the number of amino acid differences in hemoglobin between different lineages changes roughly linearly with time, as estimated from fossil evidence. They generalized this observation to assert that the rate of evolutionary change of any specified protein was approximately constant over time and over different lineages (known as the molecular clock hypothesis). The genetic equidistance phenomenon was first noted in 1963 by Emanuel Margoliash, who wrote: "It appears that the number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Additive Distance Matrix
Additive may refer to: Mathematics * Additive function, a function in number theory * Additive map, a function that preserves the addition operation * Additive set-function see Sigma additivity * Additive category, a preadditive category with finite biproducts * Additive inverse, an arithmetic concept * Additive prime, a prime number where the sum of its digits is a number which is also a prime number. Science * Additive color, as opposed to subtractive color * Additive model, a statistical regression model * Additive synthesis, an audio synthesis technique * Additive genetic effects * Additive quantity, a physical quantity that is additive for subsystems; see Intensive and extensive properties Engineering * Feed additive * Gasoline additive, a substance used to improve the performance of a fuel, lower emissions or clean the engine * Oil additive, a substance used to improve the performance of a lubricant * Weakly additive, the quality of preferences in some logistics problems * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phylogenetic Tree
A phylogenetic tree or phylogeny is a graphical representation which shows the evolutionary history between a set of species or taxa during a specific time.Felsenstein J. (2004). ''Inferring Phylogenies'' Sinauer Associates: Sunderland, MA. In other words, it is a branching diagram or a tree showing the evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical or genetic characteristics. In evolutionary biology, all life on Earth is theoretically part of a single phylogenetic tree, indicating common ancestry. Phylogenetics is the study of phylogenetic trees. The main challenge is to find a phylogenetic tree representing optimal evolutionary ancestry between a set of species or taxa. Computational phylogenetics (also phylogeny inference) focuses on the algorithms involved in finding optimal phylogenetic tree in the phylogenetic landscape. Phylogenetic trees may be rooted or unrooted. In a ''rooted'' p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bioinformatics
Bioinformatics () is an interdisciplinary field of science that develops methods and Bioinformatics software, software tools for understanding biological data, especially when the data sets are large and complex. Bioinformatics uses biology, chemistry, physics, computer science, data science, computer programming, information engineering, mathematics and statistics to analyze and interpret biological data. The process of analyzing and interpreting data can sometimes be referred to as computational biology, however this distinction between the two terms is often disputed. To some, the term ''computational biology'' refers to building and using models of biological systems. Computational, statistical, and computer programming techniques have been used for In silico, computer simulation analyses of biological queries. They include reused specific analysis "pipelines", particularly in the field of genomics, such as by the identification of genes and single nucleotide polymorphis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamming Distance
In information theory, the Hamming distance between two String (computer science), strings or vectors of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of ''substitutions'' required to change one string into the other, or equivalently, the minimum number of ''errors'' that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming. A major application is in coding theory, more specifically to block codes, in which the equal-length strings are Vector space, vectors over a finite field. Definition The Hamming distance between two equal-length strings of symbols is the number of positions at which the corresponding symbols are different. Examples The symbols may be letters, bits, or decimal digits, am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block Code
In coding theory, block codes are a large and important family of Channel coding, error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of ''all'' block codes in a unified way. Such limitations often take the form of ''bounds'' that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors. Examples of block codes are Reed–Solomon codes, Hamming codes, Hadamard codes, Expander codes, Golay code (other), Golay codes, Reed–Muller codes and Polar code (coding theory), Polar codes. These examples also belong to the class of linear codes, and hence they are called linear block codes. More particularly, these codes are known as algebraic block ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coding Theory
Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and computer data storage, data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data. There are four types of coding: # Data compression (or ''source coding'') # Error detection and correction, Error control (or ''channel coding'') # Cryptography, Cryptographic coding # Line code, Line coding Data compression attempts to remove unwanted redundancy from the data from a source in order to transmit it more efficiently. For example, DEFLATE data compression makes files small ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gower's Distance
In statistics, Gower's distance between two mixed-type objects is a similarity measure that can handle different types of data within the same dataset and is particularly useful in cluster analysis Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more Similarity measure, similar (in some specific sense defined by the ... or other multivariate statistical techniques. Data can be binary, ordinal, or continuous variables. It works by normalizing the differences between each pair of variables and then computing a weighted average of these differences. The distance was defined in 1971 by Gower and it takes values between 0 and 1 with smaller values indicating higher similarity. Definition For two objects i and j having p descriptors, the similarity S is defined as: S_ = \frac, where the w_ are non-negative weights usually set to 1 and s_ is the similarit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Distance Matrix
In mathematics, a Euclidean distance matrix is an matrix representing the spacing of a set of points in Euclidean space. For points x_1,x_2,\ldots,x_n in -dimensional space , the elements of their Euclidean distance matrix are given by squares of distances between them. That is :\begin A & = (a_); \\ a_ & = d_^2 \;=\; \lVert x_i - x_j\rVert^2 \end where \, \cdot\, denotes the Euclidean norm on . :A = \begin 0 & d_^2 & d_^2 & \dots & d_^2 \\ d_^2 & 0 & d_^2 & \dots & d_^2 \\ d_^2 & d_^2 & 0 & \dots & d_^2 \\ \vdots&\vdots & \vdots & \ddots&\vdots& \\ d_^2 & d_^2 & d_^2 & \dots & 0 \\ \end In the context of (not necessarily Euclidean) distance matrices, the entries are usually defined directly as distances, not their squares. However, in the Euclidean case, squares of distances are used to avoid computing square roots and to simplify relevant theorems and algorithms. Euclidean distance matrices are closely related to Gram matrices (matrices of dot products, describing nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |