|
Crisis (dynamical Systems)
In applied mathematics and astrodynamics, in the theory of dynamical systems, a crisis is the sudden appearance or disappearance of a strange attractor as the parameters of a dynamical system are varied. This global bifurcation occurs when a chaotic attractor comes into contact with an unstable periodic orbit or its stable manifold. As the orbit approaches the unstable orbit it will diverge away from the previous attractor, leading to a qualitatively different behaviour. Crises can produce intermittent behaviour. Grebogi, Ott, Romeiras, and Yorke distinguished between three types of crises: * The first type, a boundary or an exterior crisis, the attractor is suddenly destroyed as the parameters are varied. In the postbifurcation state the motion is transiently chaotic, moving chaotically along the former attractor before being attracted to a fixed point, periodic orbit, quasiperiodic orbit, another strange attractor, or diverging to infinity. * In the second type of crisis, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcations And Crises Of Ikeda Attractor
Bifurcation or bifurcated may refer to: Science and technology * Bifurcation theory, the study of sudden changes in dynamical systems ** Bifurcation, of an incompressible flow, modeled by squeeze mapping the fluid flow * River bifurcation, the forking of a river into its distributaries * Bifurcation lake, a lake that flows into two different drainage basins * Bifurcated bonding, a single hydrogen atom participates in two hydrogen bonds * Bifurcated stick grip, a type of aircraft control column Other uses * Bifurcation (law), the division of issues in a trial See also * Aortic bifurcation, the point at which the abdominal aorta bifurcates into the left and right common iliac arteries * Tracheal bifurcation, or the carina of trachea (Latin: ''bifurcatio tracheae'') * Bifurcation diagram * Bifurcate merging, a kinship system * False dilemma A false dilemma, also referred to as false dichotomy or false binary, is an informal fallacy based on a premise that erroneously limits wha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
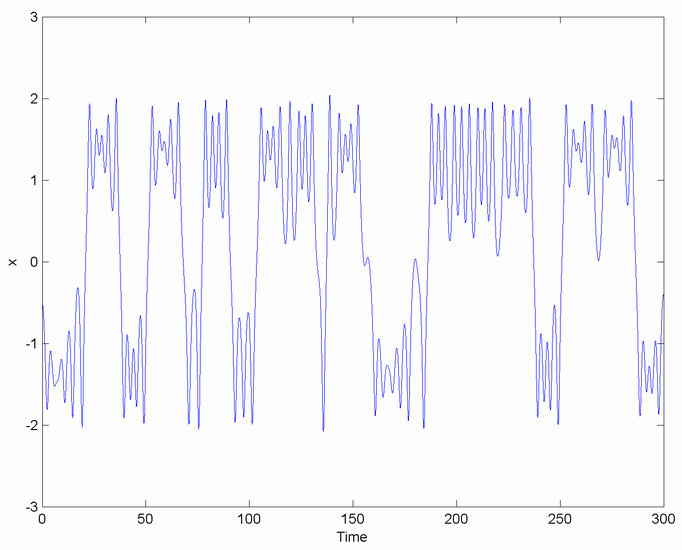
Intermittency
In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics ( Pomeau–Manneville dynamics), or different forms of chaotic dynamics (crisis-induced intermittency). Experimentally, intermittency appears as long periods of almost periodic behavior interrupted by chaotic behavior. As control variables change, the chaotic behavior become more frequent until the system is fully chaotic. This progression is known as the intermittency route to chaos. Pomeau and Manneville described three routes to intermittency where a nearly periodic system shows irregularly spaced bursts of chaos. These (type I, II and III) correspond to the approach to a saddle-node bifurcation, a subcritical Hopf bifurcation, or an inverse period-doubling bifurcation. In the apparently periodic phases the behaviour is only nearly periodic, slowly drifting away from an unstable periodic orbit. Eventually the system gets far enough away from the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Portrait
In mathematics, a phase portrait is a geometric representation of the orbits of a dynamical system in the phase plane. Each set of initial conditions is represented by a different point or curve. Phase portraits are an invaluable tool in studying dynamical systems. They consist of a plot of typical trajectories in the phase space. This reveals information such as whether an attractor, a repellor or limit cycle is present for the chosen parameter value. The concept of topological equivalence is important in classifying the behaviour of systems by specifying when two different phase portraits represent the same qualitative dynamic behavior. An attractor is a stable point which is also called a "sink". The repeller is considered as an unstable point, which is also known as a "source". A phase portrait graph of a dynamical system depicts the system's trajectories (with arrows) and stable steady states (with dots) and unstable steady states (with circles) in a phase space. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically ( fixed points, periodic orbits, or chaotic attractors) of a system as a function of a bifurcation parameter in the system. It is usual to represent stable values with a solid line and unstable values with a dotted line, although often the unstable points are omitted. Bifurcation diagrams enable the visualization of bifurcation theory. In the context of discrete-time dynamical systems, the diagram is also called orbit diagram. Logistic map An example is the bifurcation diagram of the logistic map: x_=rx_n(1-x_n). The bifurcation parameter ''r'' is shown on the horizontal axis of the plot and the vertical axis shows the set of values of the logistic function visited asymptotically from almost all initial conditions. The bifurcation diagram shows the forking of the periods of stable orbits from 1 to 2 to 4 to 8 etc. Each of these bifurcation poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intermittency
In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics ( Pomeau–Manneville dynamics), or different forms of chaotic dynamics (crisis-induced intermittency). Experimentally, intermittency appears as long periods of almost periodic behavior interrupted by chaotic behavior. As control variables change, the chaotic behavior become more frequent until the system is fully chaotic. This progression is known as the intermittency route to chaos. Pomeau and Manneville described three routes to intermittency where a nearly periodic system shows irregularly spaced bursts of chaos. These (type I, II and III) correspond to the approach to a saddle-node bifurcation, a subcritical Hopf bifurcation, or an inverse period-doubling bifurcation. In the apparently periodic phases the behaviour is only nearly periodic, slowly drifting away from an unstable periodic orbit. Eventually the system gets far enough away from the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basin Of Attraction
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed. In finite-dimensional systems, the evolving variable may be represented algebraically as an ''n''-dimensional vector. The attractor is a region in ''n''-dimensional space. In physical systems, the ''n'' dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in economic systems, they may be separate variables such as the inflation rate and the unemployment rate. If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented geometrically in two or three dimensions, (as for example in the three-dimensional case depicted to the right). An attractor can be a point, a finite set of points, a curve, a manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiperiodic Motion
In mathematics and theoretical physics, quasiperiodic motion is motion on a torus that never comes back to the same point. This behavior can also be called quasiperiodic evolution, dynamics, or flow. The torus may be a generalized torus so that the neighborhood of any point is more than two-dimensional. At each point of the torus there is a direction of motion that remains on the torus. Once a flow on a torus is defined or fixed, it determines trajectories. If the trajectories come back to a given point after a certain time then the motion is periodic with that period, otherwise it is quasiperiodic. The quasiperiodic motion is characterized by a finite set of frequencies which can be thought of as the frequencies at which the motion goes around the torus in different directions. For instance, if the torus is the surface of a doughnut, then there is the frequency at which the motion goes around the doughnut and the frequency at which it goes inside and out. But the set of frequenci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation (mathematics), transformation. Specifically, for function (mathematics), functions, a fixed point is an element that is mapped to itself by the function. Any set of fixed points of a transformation is also an invariant set. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain of a function, domain and the codomain of , and . In particular, cannot have any fixed point if its domain is disjoint from its codomain. If is defined on the real numbers, it corresponds, in graphical terms, to a curve in the Euclidean plane, and each fixed-point corresponds to an intersection of the curve with the line , cf. picture. For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set. Physical example The gravitational tidal forces acting on the rings of Saturn provide an easy-to-visualize physical example. The tidal forces flatten the ring into the equatorial plane, even as they stretch it out in the radial direction. Imagining the rings to be sand or gravel particles ("dust") in orbit around Saturn, the tidal forces are such that any perturbations that push particles above or below the equatorial plane results in that particle feeling a restoring force, pushing it back into the plane. Particles effectively oscillate in a harmonic well, damped by collisions. The stable direction is perpendicular to the ring. The unstable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the profession, professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of Mathematical analysis, applied analysis, most notably differential equations; approximation theory (broadly construed, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Orbit
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time. Iterated functions Given a mapping from a set into itself, :f: X \to X, a point in is called periodic point if there exists an >0 so that :\ f_n(x) = x where is the th iterate of . The smallest positive integer satisfying the above is called the ''prime period'' or ''least period'' of the point . If every point in is a periodic point with the same period , then is called ''periodic'' with period (this is not to be confused with the notion of a periodic function). If there exist distinct and such that :f_n(x) = f_m(x) then is called a preperiodic point. All periodic points are preperiodic. If is a diffeomorphism of a differentiable manifold, so that the derivative f_n^\prime is defined, then one says that a periodic point is ''hyperbolic'' if :, f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |