|
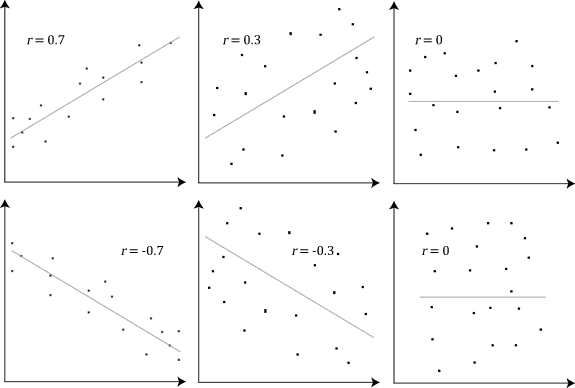
Correlations
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Examples2
In statistics, correlation or dependence is any statistical relationship, whether causality, causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are ''line (geometry), linearly'' related. Familiar examples of dependent phenomena include the correlation between the human height, height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causality, causal relationship, because extreme weather causes people to use more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
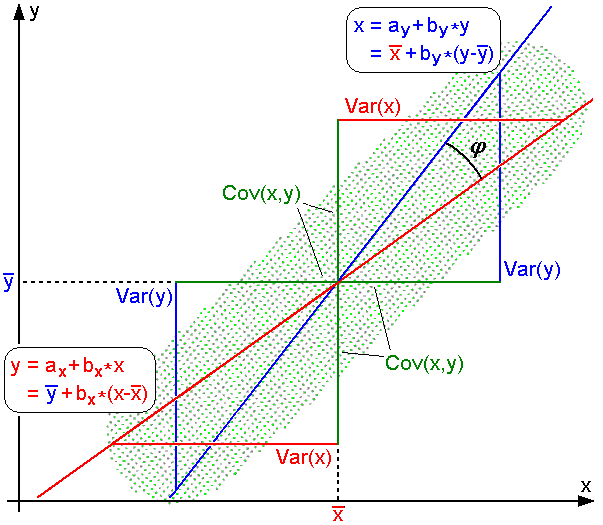
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The naming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spearman's Rank Correlation Coefficient
In statistics, Spearman's rank correlation coefficient or Spearman's ''ρ'' is a number ranging from -1 to 1 that indicates how strongly two sets of ranks are correlated. It could be used in a situation where one only has ranked data, such as a tally of gold, silver, and bronze medals. If a statistician wanted to know whether people who are high ranking in sprinting are also high ranking in long-distance running, they would use a Spearman rank correlation coefficient. The coefficient is named after Charles Spearman and often denoted by the Greek letter \rho (rho) or as r_s. It is a nonparametric measure of rank correlation ( statistical dependence between the rankings of two variables). It assesses how well the relationship between two variables can be described using a monotonic function. The Spearman correlation between two variables is equal to the Pearson correlation between the rank values of those two variables; while Pearson's correlation assesses linear relationshi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information content, amount of information" (in Units of information, units such as shannon (unit), shannons (bits), Nat (unit), nats or Hartley (unit), hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of Entropy (information theory), entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the Pearson correlation coefficient, correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Causality
Causality is an influence by which one Event (philosophy), event, process, state, or Object (philosophy), object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cause is at least partly responsible for the effect, and the effect is at least partly dependent on the cause. The cause of something may also be described as the reason for the event or process. In general, a process can have multiple causes,Compare: which are also said to be ''causal factors'' for it, and all lie in its past. An effect can in turn be a cause of, or causal factor for, many other effects, which all lie in its future. Some writers have held that causality is metaphysics , metaphysically prior to notions of time and space. Causality is an abstraction that indicates how the world progresses. As such it is a basic concept; it is more apt to be an explanation of other concepts of progression than something to be explained by other more fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Data
In statistics, bivariate data is data on each of two variables, where each value of one of the variables is paired with a value of the other variable. It is a specific but very common case of multivariate data. The association can be studied via a tabular or graphical display, or via sample statistics which might be used for inference. Typically it would be of interest to investigate the possible association between the two variables. The method used to investigate the association would depend on the level of measurement of the variable. This association that involves exactly two variables can be termed a bivariate correlation, or bivariate association. For two quantitative variables (interval or ratio in level of measurement), a scatterplot can be used and a correlation coefficient or regression model can be used to quantify the association. For two qualitative variables (nominal or ordinal in level of measurement), a contingency table can be used to view the data, and a meas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karl Pearson
Karl Pearson (; born Carl Pearson; 27 March 1857 – 27 April 1936) was an English biostatistician and mathematician. He has been credited with establishing the discipline of mathematical statistics. He founded the world's first university statistics department at University College London in 1911, and contributed significantly to the field of biometrics and meteorology. Pearson was also a proponent of Social Darwinism and eugenics, and his thought is an example of what is today described as scientific racism. Pearson was a protégé and biographer of Sir Francis Galton. He edited and completed both William Kingdon Clifford's ''Common Sense of the Exact Sciences'' (1885) and Isaac Todhunter's ''History of the Theory of Elasticity'', Vol. 1 (1886–1893) and Vol. 2 (1893), following their deaths. Early life and education Pearson was born in Islington, London, into a Quaker family. His father was William Pearson QC of the Inner Temple, and his mother Fanny (née Smit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncorrelated
In probability theory and statistics, two real-valued random variables, X, Y, are said to be uncorrelated if their covariance, \operatorname ,Y= \operatorname Y- \operatorname \operatorname /math>, is zero. If two variables are uncorrelated, there is no linear relationship between them. Uncorrelated random variables have a Pearson correlation coefficient, when it exists, of zero, except in the trivial case when either variable has zero variance (is a constant). In this case the correlation is undefined. In general, uncorrelatedness is not the same as orthogonality, except in the special case where at least one of the two random variables has an expected value of 0. In this case, the covariance is the expectation of the product, and X and Y are uncorrelated if and only if In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The bicondit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Independence
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Dependence
In the theory of vector spaces, a set of vectors is said to be if there exists no nontrivial linear combination of the vectors that equals the zero vector. If such a linear combination exists, then the vectors are said to be . These concepts are central to the definition of dimension. A vector space can be of finite dimension or infinite dimension depending on the maximum number of linearly independent vectors. The definition of linear dependence and the ability to determine whether a subset of vectors in a vector space is linearly dependent are central to determining the dimension of a vector space. Definition A sequence of vectors \mathbf_1, \mathbf_2, \dots, \mathbf_k from a vector space is said to be ''linearly dependent'', if there exist scalars a_1, a_2, \dots, a_k, not all zero, such that :a_1\mathbf_1 + a_2\mathbf_2 + \cdots + a_k\mathbf_k = \mathbf, where \mathbf denotes the zero vector. This implies that at least one of the scalars is nonzero, say a_1\ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Interval
In mathematics, a real interval is the set (mathematics), set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a Bounded set, bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite. For example, the set of real numbers consisting of , , and all numbers in between is an interval, denoted and called the unit interval; the set of all positive real numbers is an interval, denoted ; the set of all real numbers is an interval, denoted ; and any single real number is an interval, denoted . Intervals are ubiquitous in mathematical analysis. For example, they occur implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function is an interval; integrals of real functions are defined over an int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |