|
Constant Problem
In mathematics, the constant problem is the problem of deciding whether a given expression is equal to zero. The problem This problem is also referred to as the identity problem or the method of zero estimates. It has no formal statement as such but refers to a general problem prevalent in transcendental number theory. Often proofs in transcendence theory are proofs by contradiction. Specifically, they use some auxiliary function to create an integer ''n'' ≥ 0, which is shown to satisfy ''n'' < 1. Clearly, this means that ''n'' must have the value zero, and so a contradiction arises if one can show that in fact ''n'' is ''not'' zero. In many transcendence proofs, proving that ''n'' ≠ 0 is very difficult, and hence a lot of work has been done to develop methods that can be used to prove the non-vanishing of certain expressions. The sheer generality of the problem is what makes it difficult to prove general results or come up with general met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the matrix and the linear map represented, on a given basis (linear algebra), basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible matrix, invertible and the corresponding linear map is an linear isomorphism, isomorphism. However, if the determinant is zero, the matrix is referred to as singular, meaning it does not have an inverse. The determinant is completely determined by the two following properties: the determinant of a product of matrices is the product of their determinants, and the determinant of a triangular matrix is the product of its diagonal entries. The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Relation Algorithm
An integer is the number zero ( 0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number ( −1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richardson's Theorem
In mathematics, Richardson's theorem establishes the undecidability of the equality of real numbers defined by expressions involving integers, , ln 2, and exponential and sine functions. It was proved in 1968 by the mathematician and computer scientist Daniel Richardson of the University of Bath. Specifically, the class of expressions for which the theorem holds is that generated by rational numbers, the number π, the number ln 2, the variable ''x'', the operations of addition, subtraction, multiplication, composition, and the sin, exp, and abs functions. For some classes of expressions generated by other primitives than in Richardson's theorem, there exist algorithms that can determine whether an expression is zero. Statement of the theorem Richardson's theorem can be stated as follows: Let ''E'' be a set of expressions that represent \R\to\R functions. Suppose that ''E'' includes these expressions: * ''x'' (representing the identity function) * ''ex'' (representing th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
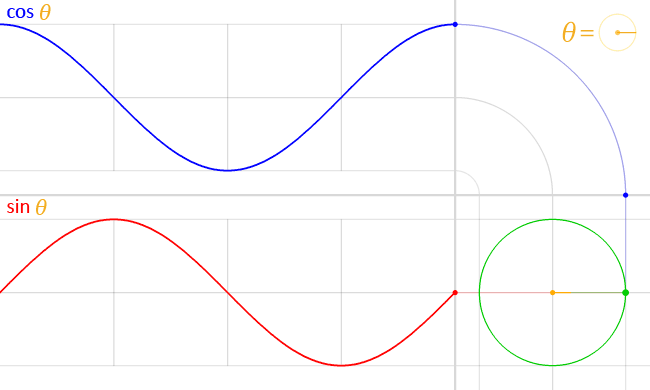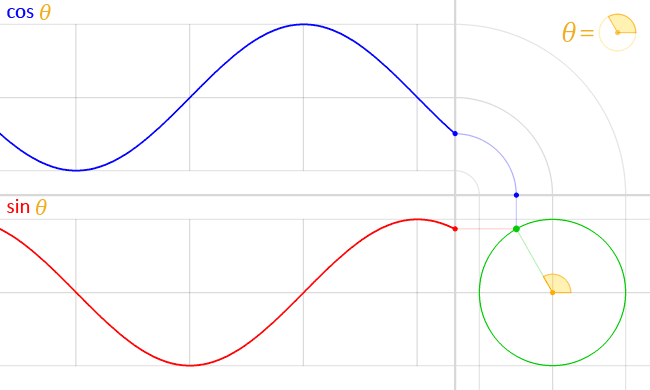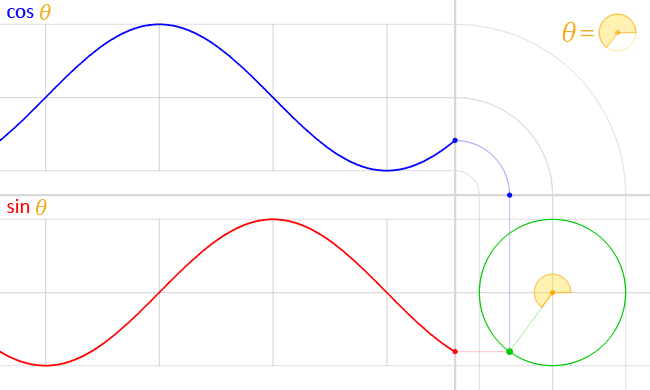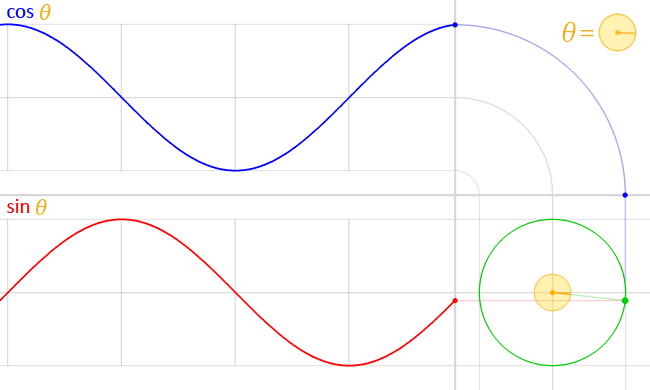
Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real number, real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as Series (mathematics), infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic function, periodic pheno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Of Computation
''Mathematics of Computation'' is a bimonthly mathematics journal focused on computational mathematics. It was established in 1943 as ''Mathematical Tables and Other Aids to Computation'', obtaining its current name in 1960. Articles older than five years are available electronically free of charge. Abstracting and indexing The journal is abstracted and indexed in Mathematical Reviews, Zentralblatt MATH, Science Citation Index, CompuMath Citation Index, and Current Contents/Physical, Chemical & Earth Sciences. According to the '' Journal Citation Reports'', the journal has a 2020 impact factor of 2.417. References External links * Delayed open access journals English-language journals Mathematics journals Academic journals established in 1943 American Mathematical Society academic journals Bimonthly journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undecidable Problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether an arbitrary program eventually halts when run. Background A decision problem is a question which, for every input in some infinite set of inputs, requires a "yes" or "no" answer. Those inputs can be numbers (for example, the decision problem "is the input a prime number?") or values of some other kind, such as strings of a formal language. The formal representation of a decision problem is a subset of the natural numbers. For decision problems on natural numbers, the set consists of those numbers that the decision problem answers "yes" to. For example, the decision problem "is the input even?" is formalized as the set of even numbers. A decision pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decidability (logic)
In logic, a true/false decision problem is decidable if there exists an effective method for deriving the correct answer. Zeroth-order logic (propositional logic) is decidable, whereas first-order and higher-order logic are not. Logical systems are decidable if membership in their set of logically valid formulas (or theorems) can be effectively determined. A theory (set of sentences closed under logical consequence) in a fixed logical system is decidable if there is an effective method for determining whether arbitrary formulas are included in the theory. Many important problems are undecidable, that is, it has been proven that no effective method for determining membership (returning a correct answer after finite, though possibly very long, time in all cases) can exist for them. Decidability of a logical system Each logical system comes with both a syntactic component, which among other things determines the notion of provability, and a semantic component, which determine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |