|
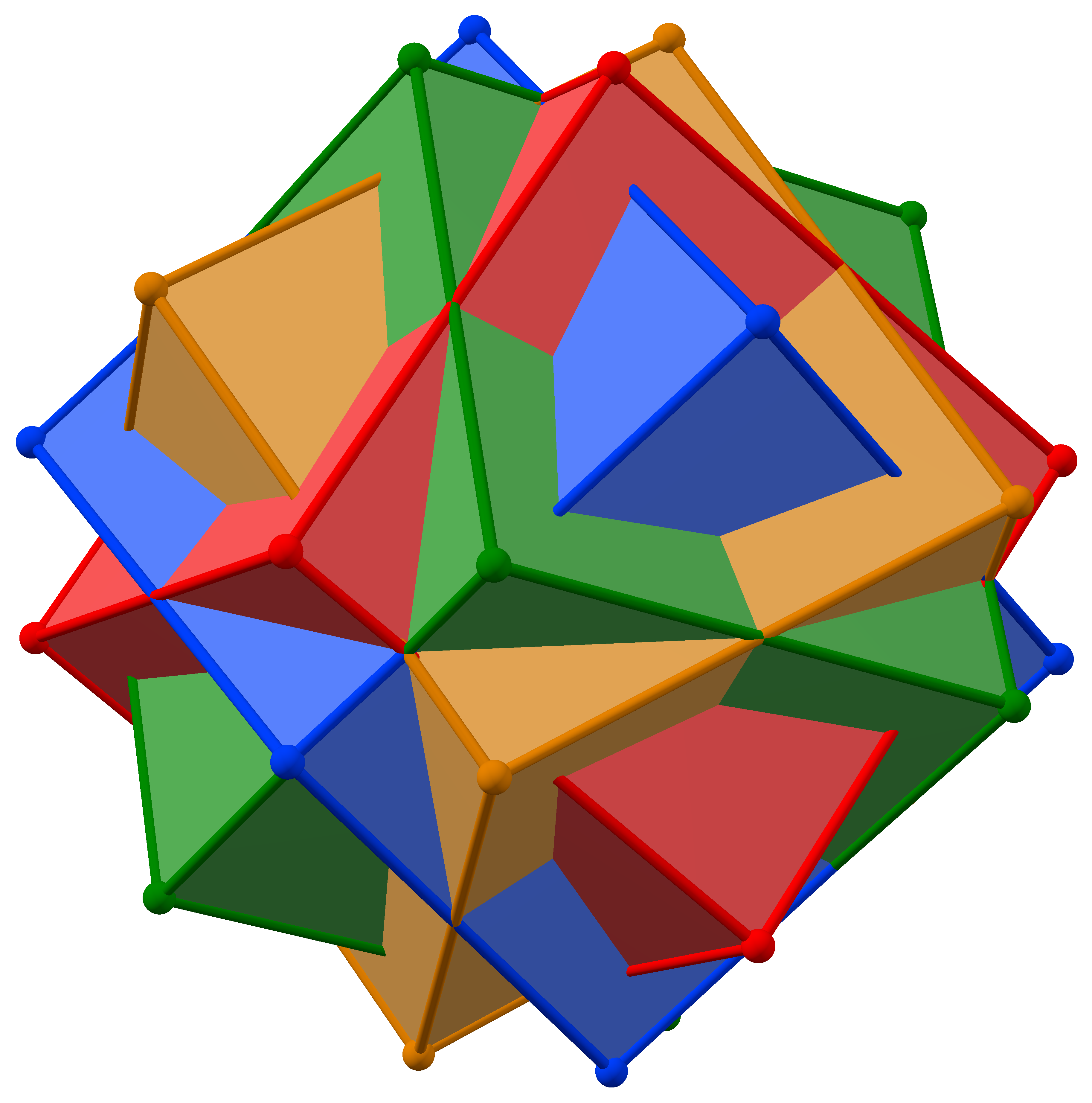
Compound Of Four Octahedra
The compound of four octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 4 octahedron, octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis (that passes through the centres of two opposite octahedral faces). Its dual is the compound of four cubes. Cartesian coordinates Cartesian coordinates for the vertices of this compound are all the permutations of : (±2, ±1, ±2) See also *Compound of three octahedra *Compound of five octahedra *Compound of ten octahedra *Compound of twenty octahedra *Compound of four cubes References *. Polyhedral compounds {{polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
UC12-4 Octahedra
UC1 may refer to: * ** , a German World War I submarine * German Type UC I submarine of World War II * , a Danish private electric sub See also * UC (other) {{Letter-NumberCombDisambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polyhedron Compound
In geometry, a uniform polyhedron compound is a polyhedral compound whose constituents are identical (although possibly enantiomorphous) uniform polyhedra, in an arrangement that is also uniform, i.e. the symmetry group of the compound acts transitively on the compound's vertices. The uniform polyhedron compounds were first enumerated by John Skilling in 1976, with a proof that the enumeration is complete. The following table lists them according to his numbering. The prismatic compounds of prisms ( UC20 and UC21) exist only when , and when and are coprime In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equiv .... The uniform prismatic compounds of antiprisms ( UC22, UC23, UC24 and UC25) exist only when , and when and are coprime. Furthermore, when , the antiprisms dege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Four Cubes
The compound of four cubes or Bakos compound is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge. Its Cartesian coordinates are (±3, ±3, ±3) and the permutations of (±5, ±1, ±1). Extension with fifth cube The eight vertices on the 3-fold symmetry axes can be seen as the vertices of a fifth cube of the same size.The Wolfram pagCube 5-Compoundshows a small picture of this extension under the name "first cube 4-compound". Also Grant Sanderson has used a picture of it to illustrate the term ''symmetry''. Referring to the images below, the four old cubes are called colored, and the new one black. Each colored cube has two opposite vertices on a 3-fold symmetry axis, which are shared with the black cube. (In the picture both 3-fold vertices of the green cube are visible.) The remaining six vertices of each colored cube correspond to the faces of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Twenty Octahedra
The compound of twenty octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra (considered as triangular antiprisms). It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide. Related polyhedra This compound shares its edge arrangement with the great dirhombicosidodecahedron, the great disnub dirhombidodecahedron, and the compound of twenty tetrahemihexahedra. It may be constructed as the exclusive or of the two enantiomorphs of the great snub dodecicosidodecahedron. See also *Compound of three octahedra *Compound of four octahedra *Compound of five octahedra The compound of five octahedra is one of the five regular polyhedron compounds, and can also be seen as a stellation. It was first described by Edmund Hess in 1876. It is unique among the regular compounds for not having a regular convex hull. ... * Compound of ten octahedra References *. Polyh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Ten Octahedra
The compounds of ten octahedra UC15 and UC16 are two uniform polyhedron compounds. They are composed of a symmetric arrangement of 10 octahedron, octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron. The two compounds differ in the orientation of their octahedra: each compound may be transformed into the other by rotating each octahedron by 60 degrees. For UC15, the convex hull of this compound is a nonuniform rhombicosidodecahedron. For UC16, the convex hull would be a nonuniform truncated icosahedron. Cartesian coordinates Cartesian coordinates for the vertices of this compound are all the cyclic permutations of : (0, ±(φ−1 + 2''s''φ), ±(φ − 2sφ−1)) : (±( − ''s''τφ2), ±( + ''s''(2τφ − 1)), ±( + ''s''φ−2)) : (±(φ−1 − ''s''φ), ±(φ + ''s''φ−1), ±3''s'') where φ = (1 + )/2 is the golden ratio and ''s'' is either +1 or −1. Settin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Five Octahedra
The compound of five octahedra is one of the five regular polyhedron compounds, and can also be seen as a stellation. It was first described by Edmund Hess in 1876. It is unique among the regular compounds for not having a regular convex hull. As a stellation It is the second stellation of the icosahedron, and given as List of Wenninger polyhedron models#Stellations of icosahedron, Wenninger model index 23. It can be constructed by a rhombic triacontahedron with rhombic-based Pyramid (geometry), pyramids added to all the faces, as shown by the five colored model image. (This construction does not generate the ''regular'' compound of five octahedra, but shares the same topology and can be smoothly deformed into the regular compound.) It has a density of greater than 1. As a compound It can also be seen as a polyhedral compound of five Octahedron, octahedra arranged in icosahedral symmetry (Ih). The spherical polyhedron, spherical and stereographic projection, stereograph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Three Octahedra
In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three octahedron, regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut ''Stars (M. C. Escher), Stars''. Construction A regular octahedron can be circumscribed around a cube in such a way that the eight edges of two opposite squares of the cube lie on the eight faces of the octahedron. The three octahedra formed in this way from the three pairs of opposite cube squares form the compound of three octahedra.. The eight cube vertices are the same as the eight points in the compound where three edges cross each other. Each of the octahedron edges that participates in these triple crossings is divided by the crossing point in the ratio 1:square root of 2, . The remaining octahedron ed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Four Cubes
The compound of four cubes or Bakos compound is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge. Its Cartesian coordinates are (±3, ±3, ±3) and the permutations of (±5, ±1, ±1). Extension with fifth cube The eight vertices on the 3-fold symmetry axes can be seen as the vertices of a fifth cube of the same size.The Wolfram pagCube 5-Compoundshows a small picture of this extension under the name "first cube 4-compound". Also Grant Sanderson has used a picture of it to illustrate the term ''symmetry''. Referring to the images below, the four old cubes are called colored, and the new one black. Each colored cube has two opposite vertices on a 3-fold symmetry axis, which are shared with the black cube. (In the picture both 3-fold vertices of the green cube are visible.) The remaining six vertices of each colored cube correspond to the faces of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
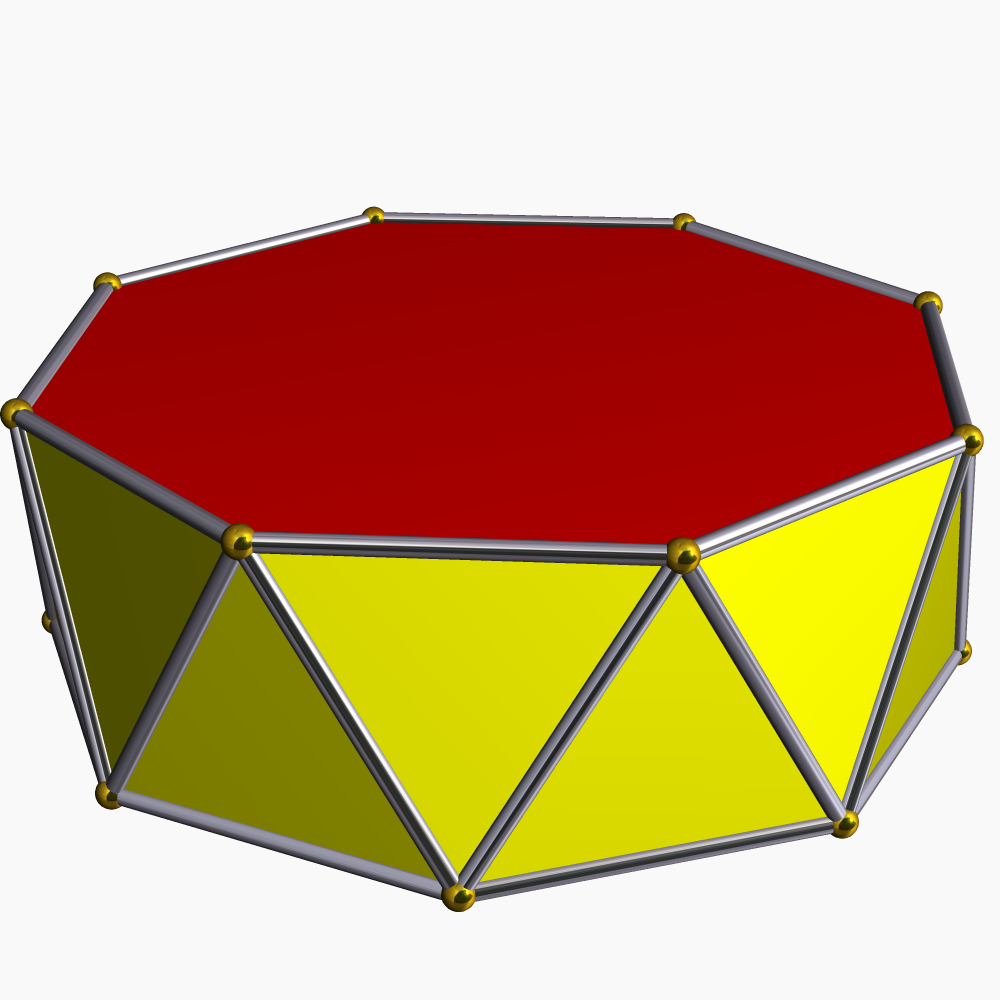
Antiprisms
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net of a hexagonal antiprism has been attributed to Hieronymus Andreae, who died in 1556. The German form of the word "antiprism" was used for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Four Octahedra
The compound of four octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 4 octahedron, octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis (that passes through the centres of two opposite octahedral faces). Its dual is the compound of four cubes. Cartesian coordinates Cartesian coordinates for the vertices of this compound are all the permutations of : (±2, ±1, ±2) See also *Compound of three octahedra *Compound of five octahedra *Compound of ten octahedra *Compound of twenty octahedra *Compound of four cubes References *. Polyhedral compounds {{polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polyhedron Compound
In geometry, a uniform polyhedron compound is a polyhedral compound whose constituents are identical (although possibly enantiomorphous) uniform polyhedra, in an arrangement that is also uniform, i.e. the symmetry group of the compound acts transitively on the compound's vertices. The uniform polyhedron compounds were first enumerated by John Skilling in 1976, with a proof that the enumeration is complete. The following table lists them according to his numbering. The prismatic compounds of prisms ( UC20 and UC21) exist only when , and when and are coprime In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equiv .... The uniform prismatic compounds of antiprisms ( UC22, UC23, UC24 and UC25) exist only when , and when and are coprime. Furthermore, when , the antiprisms dege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |