|
Book Embedding
In graph theory, a book embedding is a generalization of planar graph, planar embedding of a Graph (discrete mathematics), graph to embeddings in a ''book'', a collection of half-planes all having the same Line (geometry), line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the ''spine'', and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number. Every graph with vertices has book thickness at most \lceil n/2\rceil, and this formula gives the exact book thickness for complete graphs. The graphs with book thickness one are the outerplanar graphs. The graphs with book thickness at most two are the subhamilt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bioinformatics
Bioinformatics () is an interdisciplinary field of science that develops methods and Bioinformatics software, software tools for understanding biological data, especially when the data sets are large and complex. Bioinformatics uses biology, chemistry, physics, computer science, data science, computer programming, information engineering, mathematics and statistics to analyze and interpret biological data. The process of analyzing and interpreting data can sometimes be referred to as computational biology, however this distinction between the two terms is often disputed. To some, the term ''computational biology'' refers to building and using models of biological systems. Computational, statistical, and computer programming techniques have been used for In silico, computer simulation analyses of biological queries. They include reused specific analysis "pipelines", particularly in the field of genomics, such as by the identification of genes and single nucleotide polymorphis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sheaf Of Planes
In mathematics, a sheaf of planes is the set of all planes that have the same common line. It may also be known as a fan of planes or a '' pencil of planes''. When extending the concept of line to the ''line at infinity'', a set of ''parallel planes'' can be seen as a sheaf of planes intersecting in a line at infinity. To distinguish it from the more general definition, the adjective ''parallel'' can be added to it, resulting in the expression parallel sheaf of planes. See also *Book embedding, a notion of graph embedding onto sheafs of half-plane In mathematics, the upper half-plane, is the set of points in the Cartesian plane with The lower half-plane is the set of points with instead. Arbitrary oriented half-planes can be obtained via a planar rotation. Half-planes are an example ...s Notes {{DEFAULTSORT:Sheaf of planes Planes (geometry) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a topological space is a Set (mathematics), set whose elements are called Point (geometry), points, along with an additional structure called a topology, which can be defined as a set of Neighbourhood (mathematics), neighbourhoods for each point that satisfy some Axiom#Non-logical axioms, axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate. A topological space is the most general type of a space (mathematics), mathematical space that allows for the definition of Limit (mathematics), limits, Continuous function (topology), continuity, and Connected space, connectedness. Common types ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
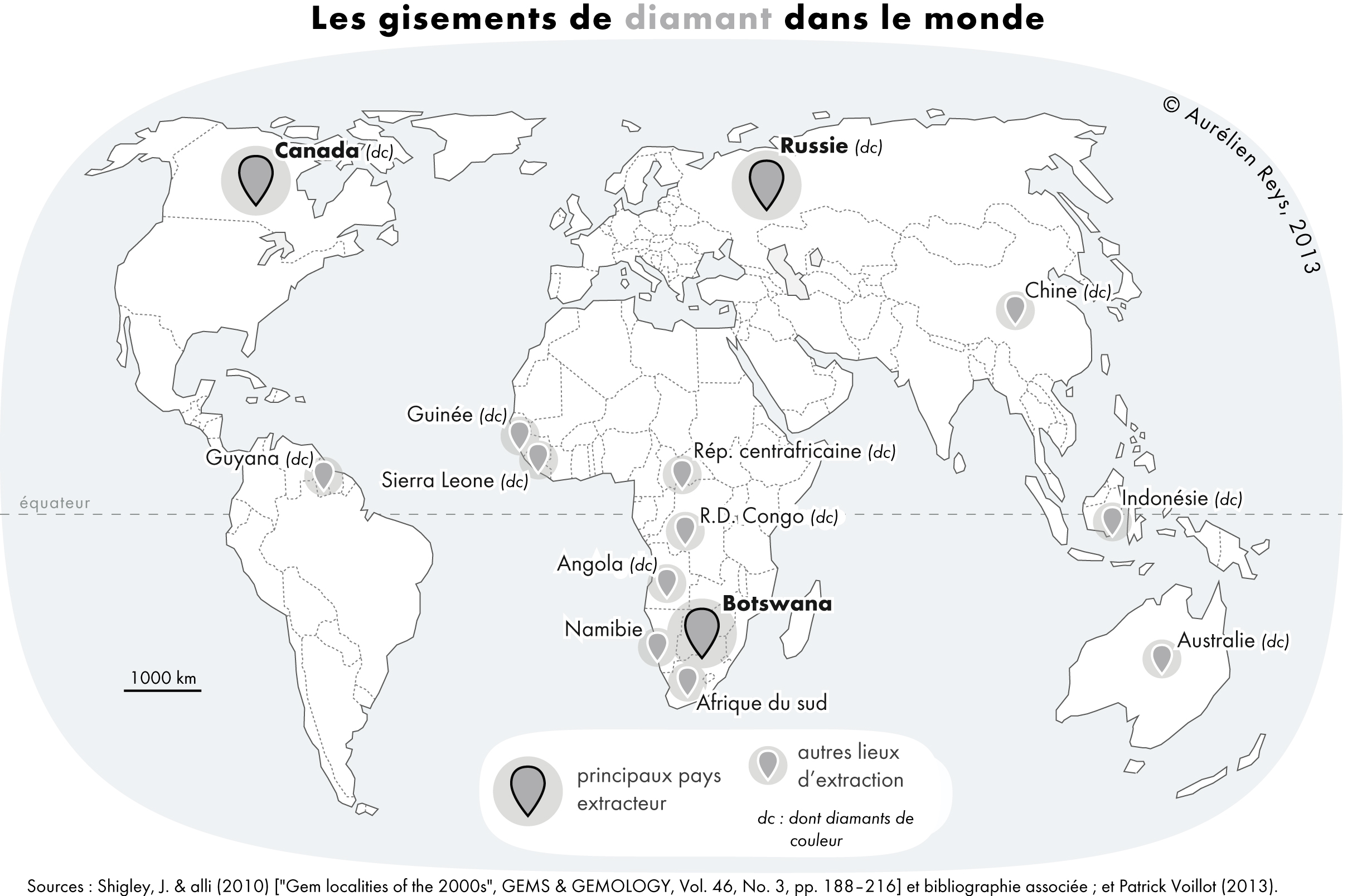
Diamond Pagewidth
Diamond is a solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Diamond is tasteless, odourless, strong, brittle solid, colourless in pure form, a poor conductor of electricity, and insoluble in water. Another solid form of carbon known as graphite is the chemically stable form of carbon at room temperature and pressure, but diamond is metastable and converts to it at a negligible rate under those conditions. Diamond has the highest hardness and thermal conductivity of any natural material, properties that are used in major industrial applications such as cutting and polishing tools. Because the arrangement of atoms in diamond is extremely rigid, few types of impurity can contaminate it (two exceptions are boron and nitrogen). Small numbers of defects or impurities (about one per million of lattice atoms) can color a diamond blue (boron), yellow (nitrogen), brown (defects), green (radiation exposure), purple, pink, oran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planar Graphs
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph, or a planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points. Every graph that can be drawn on a plane can be drawn on the sphere as well, and vice versa, by means of stereographic projection. Plane graphs can be encoded by combinatorial maps or rotation systems. An equivalence class of topologically equivalent drawings on the sphere, usually with additional assumptions such as the absence of isthmuses, is calle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mihalis Yannakakis
Mihalis Yannakakis (; born 13 September 1953 in Athens, Greece)Columbia University: CV: Mihalis Yannakakis (accessed 12 November 2009) is a professor of computer science at . He is noted for his work in , , and other related fields. He won the Donald E. Knuth Prize in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Chester Kainen
Paul Chester Kainen is an American mathematician, an adjunct associate professor of mathematics and director of the Lab for Visual Mathematics at Georgetown University. Kainen is the author of a popular book on the four color theorem, and is also known for his work on book embeddings of graphs. Biography Kainen received his Bachelor of Arts degree from George Washington University in 1966 and was awarded the Ruggles Prize for Excellence in Mathematics. He went on to get his Ph.D. from Cornell University in 1970 with Peter Hilton Peter John Hilton (7 April 1923Peter Hilton, "On all Sorts of Automorphisms", ''The American Mathematical Monthly'', 92(9), November 1985, p. 6506 November 2010) was a British mathematician, noted for his contributions to homotopy theory and f ... as his thesis advisor. Kainen's father was the American artist Jacob Kainen. Selected publications *. 2nd ed., Dover, 1986, , . *. References External linksHome pageat GeorgetownPaul Kainen's Page on I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamenta Mathematicae
''Fundamenta Mathematicae'' is a peer-reviewed scientific journal of mathematics with a special focus on the foundations of mathematics, concentrating on set theory, mathematical logic, topology and its interactions with algebra, and dynamical systems. The first specialized journal in the field of mathematics, originally it covered only topology, set theory, and foundations of mathematics..... It is published by the Mathematics Institute of the Polish Academy of Sciences. History The journal was conceived by Zygmunt Janiszewski as a means to foster mathematical research in Poland.According to and to the introduction to the 100th volume of the journal (1978, pp=1–2). These two sources cite an article written by Janiszewski himself in 1918 and titled "''On the needs of Mathematics in Poland''". Janiszewski posited that, to achieve its goal, the journal should not compel Polish mathematicians to submit articles written exclusively in Polish, and should be devoted only to a sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michigan State University
Michigan State University (Michigan State or MSU) is a public university, public Land-grant university, land-grant research university in East Lansing, Michigan, United States. It was founded in 1855 as the Agricultural College of the State of Michigan, the first of its kind in the country. After the introduction of the Morrill Land-Grant Acts, Morrill Act in 1862, the state designated the college a land-grant institution in 1863, making it the first of the land-grant colleges in the United States. The college became coeducational in 1870. Today, Michigan State has facilities all across the state and over 634,000 alumni. Michigan State is a member of the Association of American Universities and is Carnegie Classification of Institutions of Higher Education, classified among "R1: Doctoral Universities – Very high research activity". The university's campus houses the Facility for Rare Isotope Beams, the W. J. Beal Botanical Garden, the Abrams Planetarium, the Wharton Center f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |