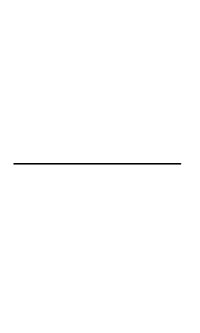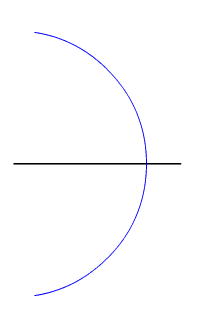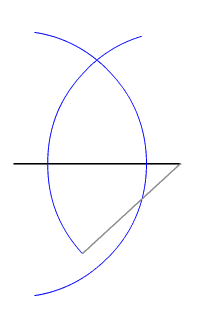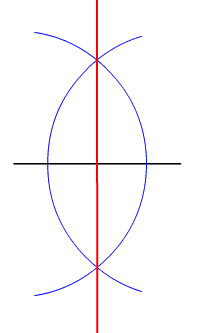|
Bisection
In geometry, bisection is the division of something into two equal or congruent parts (having the same shape and size). Usually it involves a bisecting line, also called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'', a line that passes through the midpoint of a given segment, and the ''angle bisector'', a line that passes through the apex of an angle (that divides it into two equal angles). In three-dimensional space, bisection is usually done by a bisecting plane, also called the ''bisector''. Perpendicular line segment bisector Definition *The perpendicular bisector of a line segment is a line which meets the segment at its midpoint perpendicularly. *The perpendicular bisector of a line segment AB also has the property that each of its points X is equidistant from segment AB's endpoints: (D)\quad , XA, = , XB, . The proof follows from , MA, =, MB, and Pythagoras' theorem: :, XA, ^2=, XM, ^2+, MA, ^2=, XM, ^2+, MB, ^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Straightedge And Compass
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a compass. The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so it may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Trisection
Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a Compass (drawing tool), compass. In 1837, Pierre Wantzel proved that the problem, as stated, is Proof of impossibility, impossible to solve for arbitrary angles. However, some special angles can be trisected: for example, it is trivial to trisect a right angle. It is possible to trisect an arbitrary angle by using tools other than straightedge and compass. For example, neusis construction, also known to ancient Greeks, involves simultaneous sliding and rotation of a marked straightedge, which cannot be achieved with the original tools. Other techniques were developed by mathematicians over the centuries. Because it is defined in simple terms, but complex to prove unsolvable, the problem of angle trisection is a frequent subject of pse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bisection Construction
In geometry, bisection is the division of something into two equal or congruent parts (having the same shape and size). Usually it involves a bisecting line, also called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'', a line that passes through the midpoint of a given segment, and the ''angle bisector'', a line that passes through the apex of an angle (that divides it into two equal angles). In three-dimensional space, bisection is usually done by a bisecting plane, also called the ''bisector''. Perpendicular line segment bisector Definition *The perpendicular bisector of a line segment is a line which meets the segment at its midpoint perpendicularly. *The perpendicular bisector of a line segment AB also has the property that each of its points X is equidistant from segment AB's endpoints: (D)\quad , XA, = , XB, . The proof follows from , MA, =, MB, and Pythagoras' theorem: :, XA, ^2=, XM, ^2+, MA, ^2=, XM, ^2+, MB, ^2=, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Midpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment. Formula The midpoint of a segment in ''n''-dimensional space whose endpoints are A = (a_1, a_2, \dots , a_n) and B = (b_1, b_2, \dots , b_n) is given by :\frac. That is, the ''i''th coordinate of the midpoint (''i'' = 1, 2, ..., ''n'') is :\frac 2. Construction Given two points of interest, finding the midpoint of the line segment they determine can be accomplished by a compass and straightedge construction. The midpoint of a line segment, embedded in a plane, can be located by first constructing a lens using circular arcs of equal (and large enough) radii centered at the two endpoints, then connecting the cusps of the lens (the two points where the arcs intersect). The point where the line connecting the cusps intersects the segment is then the midpoint of the segment. It i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude (mathematics), magnitude or Physical quantity, quantity of these types of geometric figures and in this context an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equidistant
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal. In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in ''n''-space is an (''n''−1)-space. For a triangle the circumcentre is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. This result can be generalised to cyclic polygons: the circumcentre is equidistant from each of the vertices. Likewise, the incentre of a triangle or any other tangential polygon is equidistant from the points of tangency of the polygon's sides with the circle. Every point on a perpendicular bisector of the side of a triangle or other polygon is equi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supplementary Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude or quantity of these types of geometric figures and in this context an angle consists of a number and unit of measurement. Angular measure or measure of angle are sometimes used to distinguish between the measurement and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equality (mathematics)
In mathematics, equality is a relationship between two quantities or Expression (mathematics), expressions, stating that they have the same value, or represent the same mathematical object. Equality between and is written , and read " equals ". In this equality, and are distinguished by calling them ''sides of an equation, left-hand side'' (''LHS''), and ''right-hand side'' (''RHS''). Two objects that are not equal are said to be distinct. Equality is often considered a primitive notion, meaning it is not formally defined, but rather informally said to be "a relation each thing bears to itself and nothing else". This characterization is notably circular ("nothing else"), reflecting a general conceptual difficulty in fully characterizing the concept. Basic properties about equality like Reflexive relation, reflexivity, Symmetric relation, symmetry, and Transitive relation, transitivity have been understood intuitively since at least the ancient Greeks, but were not symboli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray (geometry)
In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word ''line'' may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points (its ''endpoints''). Euclid's ''Elements'' defines a straight line as a "breadthless length" that "lies evenly with respect to the points on itself", and introduced several postulates as basic unprovable properties on which the rest of geometry was established. ''Euclidean line'' and ''Euclidean geometry'' are terms introduced to avoid confusion with generalizations introduced since the end of the 19th century, such as non-Euclidean, projective, and affine geometry. Properties In the Greek deductive geometry of Euclid's ''Elements'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |