|
Bending
In applied mechanics, bending (also known as flexure) characterizes the behavior of a slender structural element subjected to an external Structural load, load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two.Boresi, A. P. and Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced mechanics of materials, John Wiley and Sons, New York. When the length is considerably longer than the width and the thickness, the element is called a Beam (structure), beam. For example, a closet rod Deflection (engineering), sagging under the weight of clothes on clothes hangers is an example of a beam experiencing bending. On the other hand, a wikt:shell, shell is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the 'wall') is considerably smaller. A l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bending Moment
In solid mechanics, a bending moment is the Reaction (physics), reaction induced in a structural element when an external force or Moment of force, moment is applied to the element, causing the element to bending, bend. The most common or simplest structural element subjected to bending moments is the Beam (structure), beam. The diagram shows a beam which is simply supported (free to rotate and therefore lacking bending moments) at both ends; the ends can only react to the Shear stress, shear loads. Other beams can have both ends fixed (known as encastre beam); therefore each end support has both bending moments and shear reaction loads. Beams can also have one end fixed and one end simply supported. The simplest type of beam is the cantilever, which is fixed at one end and is free at the other end (neither simple nor fixed). In reality, beam supports are usually neither absolutely fixed nor absolutely rotating freely. The internal reaction loads in a cross section (geometry), cr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bending Of Plates
Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load. Bending of Kirchhoff-Love plates Definitions For a thin rectangular plate of thickness H, Young's modulus E, and Poisson's ratio \nu, we can define parameters in terms of the plate deflection, w. The flexural rigidity is given by : D = \frac Moments The bending moments per unit length are given by : M_ = -D \left( \frac + \nu \frac \right) : M_ = -D \left( \nu \frac + \frac \right) The twisting moment per unit length is given by : M_ = -D \left( 1 - \nu \right) \frac Forces The shear fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plate Theory
In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draw on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions.Timoshenko, S. and Woinowsky-Krieger, S. "Theory of plates and shells". McGraw–Hill New York, 1959. The typical thickness to width ratio of a plate structure is less than 0.1. A plate theory takes advantage of this disparity in length scale to reduce the full three-dimensional solid mechanics problem to a two-dimensional problem. The aim of plate theory is to calculate the deformation and stresses in a plate subjected to loads. Of the numerous plate theories that have been developed since the late 19th century, two are widely accepted and used in engineering. These are * the Kirchhoff–Love theory of plates (classical plate theory) * The Reissner-Mindlin theory of plates (first-order shear plate theory) Kirchhoff–Love theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Strength
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the Stress (mechanics), stress in a material just before it Yield (engineering), yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol \sigma. Introduction When an object is formed of a single material, like a wooden beam or a steel rod, is bent (Fig. 1), it experiences a range of stresses across its depth (Fig. 2). At the edge of the object on the inside of the bend (concave face) the stress will be at its maximum compressive stress value. At the outside of the bend (convex face) the stress will b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pure Bending
In solid mechanics Solid mechanics (also known as mechanics of solids) is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation (mechanics), deformation under the action of forces, temperature chang ..., pure bending (also known as the theory of simple bending) is a condition of Stress (mechanics), stress where a bending moment is applied to a Beam (structure), beam without the simultaneous presence of Cylinder stress, axial, Shear stress, shear, or Torsion (mechanics), torsional forces. Pure bending occurs only under a constant bending moment () since the shear force (), which is equal to \tfrac, has to be equal to zero. In reality, a state of pure bending does Idealization (philosophy of science), not practically exist, because such a state needs an absolutely weightless member. The state of pure bending is an approximation made to derive formulas. Kinematics of pure bending #In pure bending the axial lines ben ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plastic Bending
{{Short description, Behavior of some ductile materials Plastic bending is a nonlinear behavior particular to members made of ductile materials that frequently achieve much greater ultimate bending strength than indicated by a linear elastic bending analysis. In both the plastic and elastic bending analyses of a straight beam, it is assumed that the strain distribution is linear about the neutral axis (plane sections remain plane). In an elastic analysis this assumption leads to a linear stress distribution but in a plastic analysis the resulting stress distribution is nonlinear and is dependent on the beam's material. The limiting plastic bending strength M_r (see Plastic moment) can generally be thought of as an upper limit to a beam's load–carrying capability as it only represents the strength at a particular cross–section and not the load–carrying capability of the overall beam. A beam may fail due to global or local instability before M_r is reached at any point on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beam (structure)
A beam is a structural element that primarily resists loads applied laterally across the beam's axis (an element designed to carry a load pushing parallel to its axis would be a strut or column). Its mode of deflection is primarily by bending, as loads produce reaction forces at the beam's support points and internal bending moments, shear, stresses, strains, and deflections. Beams are characterized by their manner of support, profile (shape of cross-section), equilibrium conditions, length, and material. Beams are traditionally descriptions of building or civil engineering structural elements, where the beams are horizontal and carry vertical loads. However, any structure may contain beams, such as automobile frames, aircraft components, machine frames, and other mechanical or structural systems. Any structural element, in any orientation, that primarily resists loads applied laterally across the element's axis is a beam. Overview Historically a beam is a squared ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutral Axis
The neutral axis is an axis in the cross section of a beam (a member resisting bending) or shaft along which there are no longitudinal stresses or strains. Theory If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid of a beam or shaft. All fibers on one side of the neutral axis are in a state of tension, while those on the opposite side are in compression. Since the beam is undergoing uniform bending, a plane on the beam remains plane. That is: \gamma_=\gamma_=\tau_=\tau_=0 Where \gamma is the shear strain and \tau is the shear stress There is a compressive (negative) strain at the top of the beam, and a tensile (positive) strain at the bottom of the beam. Therefore, by the Intermediate Value Theorem, there must be some point in between the top and the bottom that has no strain, since the strain in a beam is a continuous function. Let L be the original length of the beam ( span) ε(y) is the stra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensile Stress
In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to ''tensile'' stress and may undergo elongation. An object being pushed together, such as a crumpled sponge, is subject to ''compressive'' stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has dimension of force per area, with SI units of newtons per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while ''strain'' is the measure of the relative deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such as biological organisms, minerals and chemicals. Abstract structures include data structures in computer science and musical form. Types of structure include a hierarchy (a cascade of one-to-many relationships), a network featuring many-to-many links, or a lattice featuring connections between components that are neighbors in space. Load-bearing Buildings, aircraft, skeletons, anthills, beaver dams, bridges and salt domes are all examples of load-bearing structures. The results of construction are divided into buildings and non-building structures, and make up the infrastructure of a human society. Built structures are broadly divided by their varying design approaches and standards, into categories including building structures ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deflection (engineering)
In structural engineering, deflection is the degree to which a part of a long structural element (such as Beam (structure), beam) is deformation (mechanics), deformed laterally (in the direction transverse to its longitudinal axis) under a Structural load, load. It may be quantified in terms of an angle (angular displacement) or a distance (linear displacement (geometry), displacement). A longitudinal deformation (in the direction of the axis) is called ''elongation (mechanics), elongation''. The deflection distance of a member under a load can be calculated by Integral, integrating the function that mathematically describes the slope of the deflected shape of the member under that load. Standard formulas exist for the deflection of common Beam (structure), beam configurations and load cases at discrete locations. Otherwise methods such as virtual work, Direct integration of a beam, direct integration, Castigliano's method, Macaulay's method or the direct stiffness method are use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
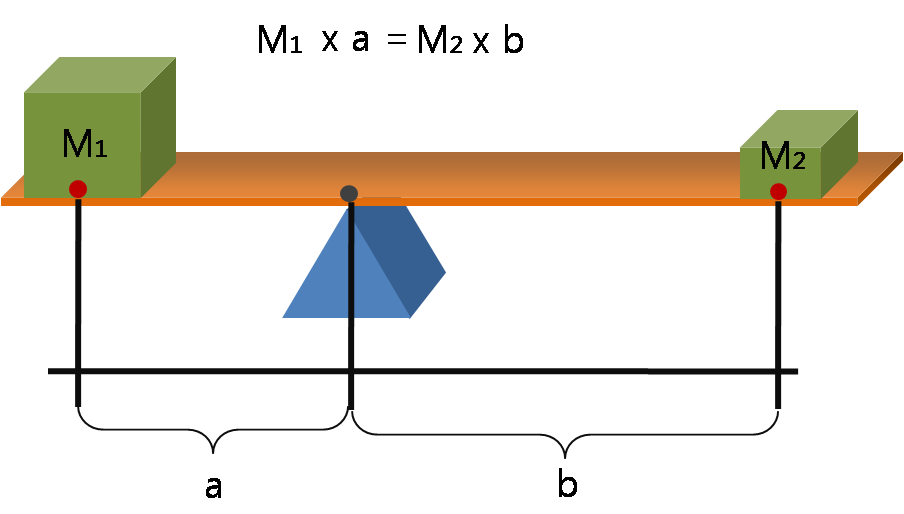
Moment (physics)
A moment is a mathematical expression involving the product of a distance and a physical quantity such as a force or electric charge. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions; a list of examples is provided later. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity is not concen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |