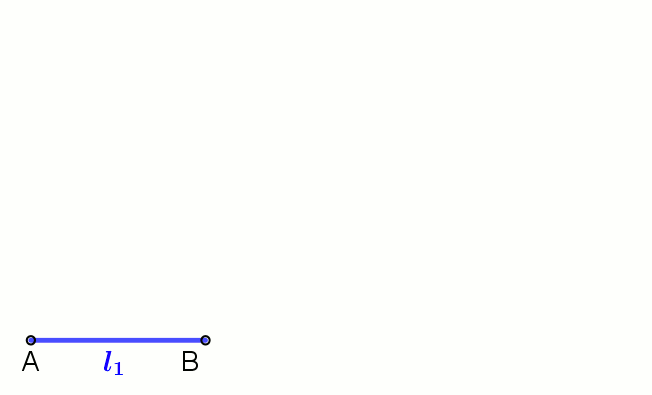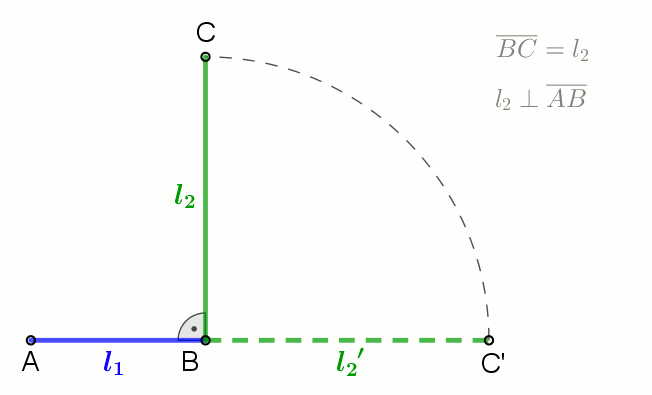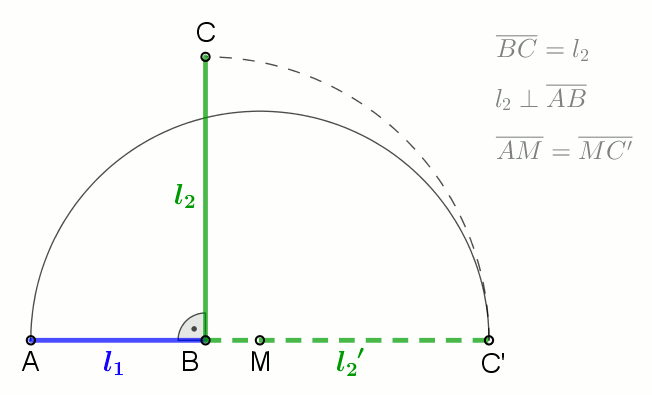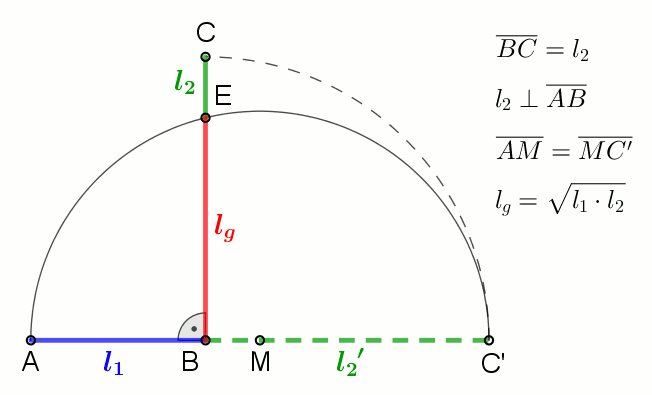|
Averaged
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly influe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired. The harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations. As a simple example, the harmonic mean of 1, 4, and 4 is : \left(\frac\right)^ = \frac = \frac = 2\,. Definition The harmonic mean ''H'' of the positive real numbers x_1, x_2, \ldots, x_n is defined to be :H = \frac = \frac = \left(\frac\right)^. The third formula in the above equation expresses the harmonic mean as the reciprocal of the arithmetic mean of the reciprocals. From the following formula: :H = \frac. it is more apparent that the harmonic mean is related to the arithmetic and geometric means. It is the reciprocal dual of the arithmetic mean for positive inputs: :1/H(1/x_1 \ldots 1/x_n) = A(x_1 \ldots x_n) The harmonic mean is a Schur-con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Experiment
An experiment is a procedure carried out to support or refute a hypothesis, or determine the efficacy or likelihood of something previously untried. Experiments provide insight into Causality, cause-and-effect by demonstrating what outcome occurs when a particular factor is manipulated. Experiments vary greatly in goal and scale but always rely on repeatable procedure and logical analysis of the results. There also exist natural experiment, natural experimental studies. A child may carry out basic experiments to understand how things fall to the ground, while teams of scientists may take years of systematic investigation to advance their understanding of a phenomenon. Experiments and other types of hands-on activities are very important to student learning in the science classroom. Experiments can raise test scores and help a student become more engaged and interested in the material they are learning, especially when used over time. Experiments can vary from personal and in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling (statistics)
In statistics, quality assurance, and survey methodology, sampling is the selection of a subset (a statistical sample) of individuals from within a statistical population to estimate characteristics of the whole population. Statisticians attempt to collect samples that are representative of the population in question. Sampling has lower costs and faster data collection than measuring the entire population and can provide insights in cases where it is infeasible to measure an entire population. Each observation measures one or more properties (such as weight, location, colour or mass) of independent objects or individuals. In survey sampling, weights can be applied to the data to adjust for the sample design, particularly in stratified sampling. Results from probability theory and statistical theory are employed to guide the practice. In business and medical research, sampling is widely used for gathering information about a population. Acceptance sampling is used to determine if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Summation Operator
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined. Summations of infinite sequences are called series. They involve the concept of limit, and are not considered in this article. The summation of an explicit sequence is denoted as a succession of additions. For example, summation of is denoted , and results in 9, that is, . Because addition is associative and commutative, there is no need of parentheses, and the result is the same irrespective of the order of the summands. Summation of a sequence of only one element results in this element itself. Summation of an empty sequence (a sequence with no elements), by convention, results in 0. Very often, the element ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Summation
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined. Summations of infinite sequences are called series. They involve the concept of limit, and are not considered in this article. The summation of an explicit sequence is denoted as a succession of additions. For example, summation of is denoted , and results in 9, that is, . Because addition is associative and commutative, there is no need of parentheses, and the result is the same irrespective of the order of the summands. Summation of a sequence of only one element results in this element itself. Summation of an empty sequence (a sequence with no elements), by convention, results in 0. Very often, the elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Population
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypothetical and potentially infinite group of objects conceived as a generalization from experience (e.g. the set of all possible hands in a game of poker). A common aim of statistical analysis is to produce information about some chosen population. In statistical inference, a subset of the population (a statistical ''sample'') is chosen to represent the population in a statistical analysis. Moreover, the statistical sample must be unbiased and accurately model the population (every unit of the population has an equal chance of selection). The ratio of the size of this statistical sample to the size of the population is called a ''sampling fraction''. It is then possible to estimate the ''population parameters'' using the appropriate sample s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Mean
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypothetical and potentially infinite group of objects conceived as a generalization from experience (e.g. the set of all possible hands in a game of poker). A common aim of statistical analysis is to produce information about some chosen population. In statistical inference, a subset of the population (a statistical ''sample'') is chosen to represent the population in a statistical analysis. Moreover, the statistical sample must be unbiased and accurately model the population (every unit of the population has an equal chance of selection). The ratio of the size of this statistical sample to the size of the population is called a ''sampling fraction''. It is then possible to estimate the ''population parameters'' using the appropriate sample st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Alphabet
The Greek alphabet has been used to write the Greek language since the late 9th or early 8th century BCE. It is derived from the earlier Phoenician alphabet, and was the earliest known alphabetic script to have distinct letters for vowels as well as consonants. In Archaic Greece, Archaic and early Classical Greece, Classical times, the Greek alphabet existed in Archaic Greek alphabets, many local variants, but, by the end of the 4th century BCE, the Euclidean alphabet, with 24 letters, ordered from alpha to omega, had become standard and it is this version that is still used for Greek writing today. The letter case, uppercase and lowercase forms of the 24 letters are: : , , , , , , , , , , , , , , , , , /ς, , , , , , . The Greek alphabet is the ancestor of the Latin script, Latin and Cyrillic scripts. Like Latin and Cyrillic, Greek originally had only a single form of each letter; it developed the letter case distinction between uppercase and lowercase in parallel with Latin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample Mean
The sample mean (or "empirical mean") and the sample covariance are statistics computed from a Sample (statistics), sample of data on one or more random variables. The sample mean is the average value (or mean, mean value) of a sample (statistics), sample of numbers taken from a larger Statistical population, population of numbers, where "population" indicates not number of people but the entirety of relevant data, whether collected or not. A sample of 40 companies' sales from the Fortune 500 might be used for convenience instead of looking at the population, all 500 companies' sales. The sample mean is used as an estimator for the population mean, the average value in the entire population, where the estimate is more likely to be close to the population mean if the sample is large and representative. The reliability of the sample mean is estimated using the standard error, which in turn is calculated using the variance of the sample. If the sample is random, the standard error fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median
In statistics and probability theory, the median is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as "the middle" value. The basic feature of the median in describing data compared to the mean (often simply described as the "average") is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of a "typical" value. Median income, for example, may be a better way to suggest what a "typical" income is, because income distribution can be very skewed. The median is of central importance in robust statistics, as it is the most resistant statistic, having a breakdown point of 50%: so long as no more than half the data are contaminated, the median is not an arbitrarily large or small result. Finite data set of numbers The median of a finite list of numbers is the "middle" number, when those numbers are list ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |