|
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Snub Polyhedron
In geometry, a snub polyhedron is a polyhedron obtained by performing a Snub (geometry), snub operation: alternation (geometry), alternating a corresponding omnitruncation, omnitruncated or truncation (geometry), truncated polyhedron, depending on the definition. Some, but not all, authors include antiprisms as snub polyhedra, as they are obtained by this construction from a degenerate "polyhedron" with only two faces (a dihedron). Chirality (mathematics), Chiral snub polyhedra do not always have reflection symmetry and hence sometimes have two ''enantiomorphous'' (left- and right-handed) forms which are reflections of each other. Their symmetry groups are all Point_groups_in_three_dimensions#The seven remaining point groups, point groups. For example, the snub cube: Snub polyhedra have Wythoff symbol and by extension, vertex configuration . Retrosnub polyhedra (a subset of the snub polyhedron, containing the great icosahedron, small retrosnub icosicosidodecahedron, and grea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements, Euclid's ''Elements''. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms". However, this definition has been criticized for not being specific enough in regard to the nature of the bases (a cause of some confusion amongst generations of later geometry writers). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprismatic Symmetry
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih''n'' (for ''n'' ≥ 2). Types There are 3 types of dihedral symmetry in three dimensions, each shown below in 3 notations: Schönflies notation, Coxeter notation, and orbifold notation. ;Chiral: *''Dn'', 'n'',2sup>+, (22''n'') of order 2''n'' – dihedral symmetry or para-n-gonal group (abstract group: ''Dihn''). ;Achiral: *''Dnh'', 'n'',2 (*22''n'') of order 4''n'' – prismatic symmetry or full ortho-n-gonal group (abstract group: ''Dihn'' × ''Z''2). *''Dnd'' (or ''Dnv''), ''n'',2+ (2*''n'') of order 4''n'' – antiprismatic symmetry or full gyro-n-gonal group (abstract group: ''Dih''2''n''). For a given ''n'', all three have ''n''-fold rotational symmetry about one axis (rotation by an angle of 360°/''n'' does not change the object), and 2-fold rotational symmetr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
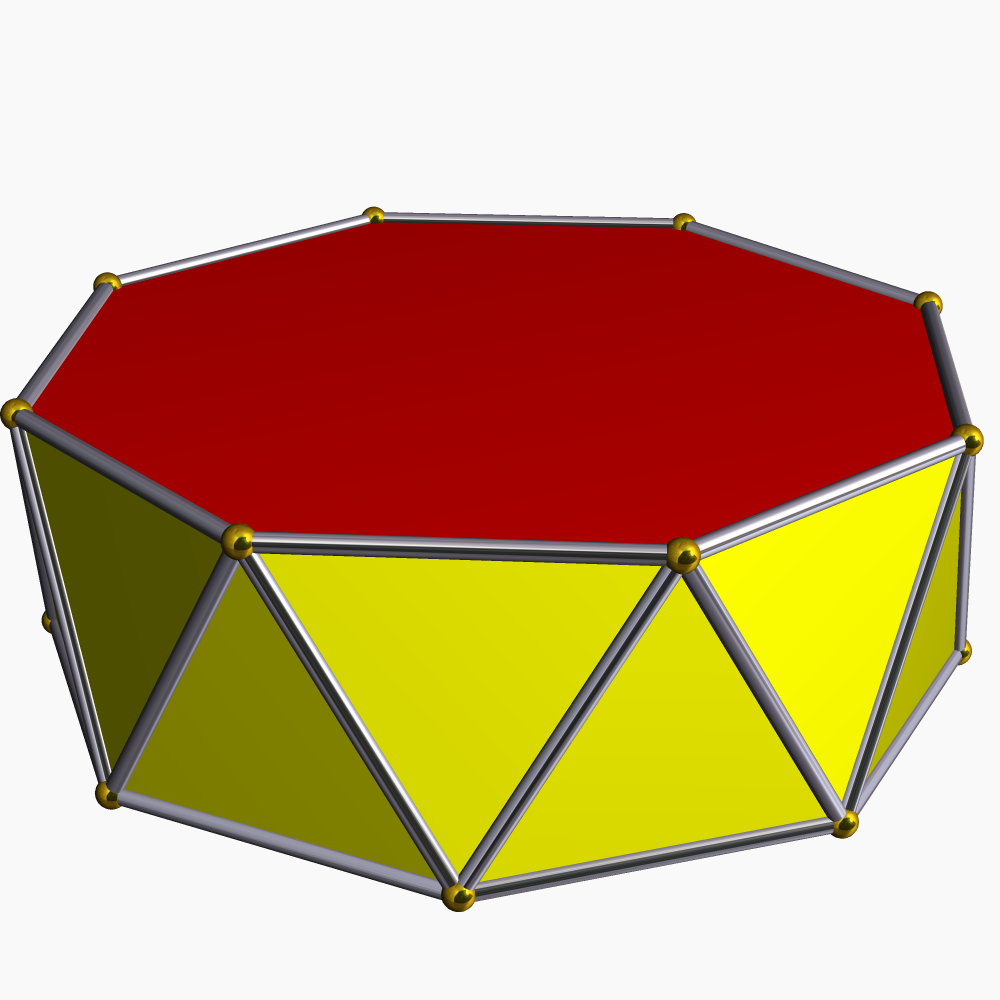
Hexagonal Antiprism
In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. Antiprisms are similar to prism (geometry), prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals. In the case of a regular ''n''-sided base, one usually considers the case where its copy is twisted by an angle . Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two bases and, connecting those bases, isosceles triangles. If faces are all regular, it is a semiregular polyhedron. Crossed antiprism A crossed hexagonal antiprism is a star polyhedron, topologically identical to the convex ''hexagonal antiprism'' with the same vertex arrangement, but it can't be made uniform; the sides are isosceles triangles. Its vertex configuration is 3.3/2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trapezohedron
In geometry, an trapezohedron, -trapezohedron, -antidipyramid, -antibipyramid, or -deltohedron Remarks: the faces of a deltohedron are deltoids; a (non-twisted) kite or deltoid can be Dissection (geometry), dissected into two isosceles triangles or "deltas" (Δ), base-to-base. is the dual polyhedron of an antiprism. The faces of an are Congruence (geometry), congruent and symmetrically staggered; they are called #Symmetry, ''twisted kites''. With a higher symmetry, its faces are Kite (geometry), ''kites'' (sometimes also called ''trapezoids'', or ''deltoids''). The "" part of the name does not refer to faces here, but to two arrangements of each Vertex (geometry), vertices around an axis of symmetry. The dual antiprism has two actual faces. An trapezohedron can be Dissection (geometry), dissected into two equal Pyramid (geometry), pyramids and an antiprism. Terminology These figures, sometimes called deltohedra, are not to be confused with Deltahedron, deltahedra, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
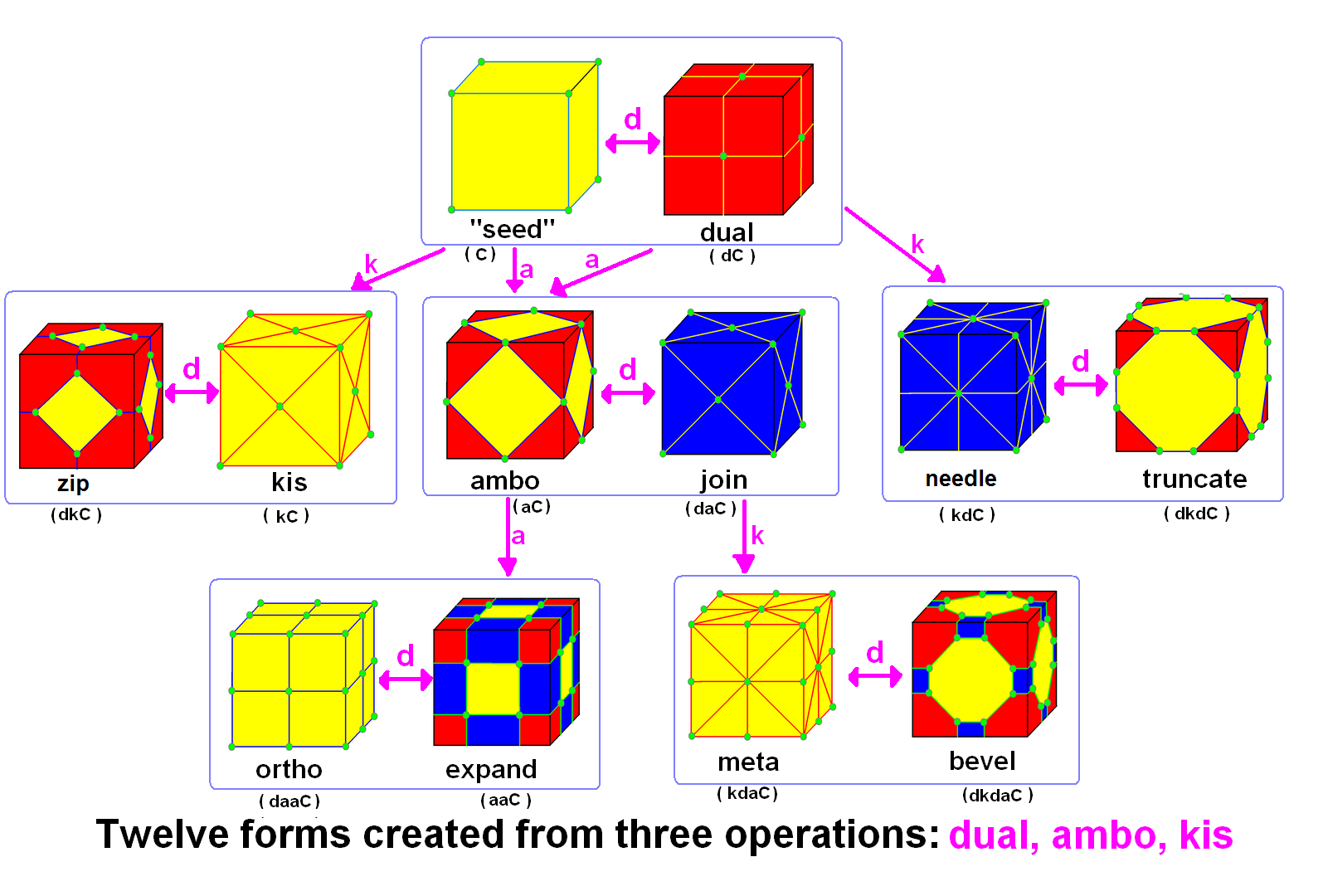
Conway Polyhedron Notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Groups In Three Dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group (mathematics), group of all isometry, isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrix, orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries. Symmetry groups of geometric objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetry, symmetries. All isometries of a Bounded set, bounded (finite) 3D object have one or more common fixed points. We follow the usual convention by choosing the Origin (mathematics), origin as one of them. The symmetry group of an object is sometimes also called its full symmetry group, as opposed to its proper symmetry group, the intersection of its full symmetry group with Euclidean group#Direct and indirect is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prismatoid
In geometry, a prismatoid is a polyhedron whose vertex (geometry), vertices all lie in two parallel Plane (geometry), planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid. Volume If the areas of the two parallel faces are and , the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is , and the height (the distance between the two parallel faces) is , then the volume of the prismatoid is given by V = \frac. This formula follows immediately by integral, integrating the area parallel to the two planes of vertices by Simpson's rule, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic function in the height. Prismatoid families Families of prismatoids include: *Pyramid (geometry), Pyramids, in which one plane con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex polygon, convex'' or ''star polygon, star''. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties These properties apply to all regular polygons, whether convex or star polygon, star: *A regular ''n''-sided polygon has rotational symmetry of order ''n''. *All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. *Together with the property of equal-length sides, this implies that every regular polygon also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |