|
Antidifference
In discrete calculus the indefinite sum operator (also known as the antidifference operator), denoted by \sum _x or \Delta^ , is the linear operator, inverse of the forward difference operator \Delta . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus :\Delta \sum_x f(x) = f(x) \, . More explicitly, if \sum_x f(x) = F(x) , then :F(x+1) - F(x) = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''F''(''x'')+''C''(''x'') for any periodic function ''C''(''x'') with period 1. Therefore, each indefinite sum actually represents a family of functions. However, due to the Carlson's theorem, the solution equal to its Newton series expansion is unique up to an additive constant ''C''. This unique solution can be represented by formal power series form of the antidifference operator: \Delta^=\frac1. Fundamental theorem of discrete calculus Indefinite sums can be used to calcu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Differences
A finite difference is a mathematical expression of the form . Finite differences (or the associated difference quotients) are often used as approximations of derivatives, such as in numerical differentiation. The difference operator, commonly denoted \Delta, is the operator (mathematics), operator that maps a function to the function \Delta[f] defined by \Delta[f](x) = f(x+1)-f(x). A difference equation is a functional equation that involves the finite difference operator in the same way as a differential equation involves derivatives. There are many similarities between difference equations and differential equations. Certain Recurrence relation#Relationship to difference equations narrowly defined, recurrence relations can be written as difference equations by replacing iteration notation with finite differences. In numerical analysis, finite differences are widely used for #Relation with derivatives, approximating derivatives, and the term "finite difference" is often used a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
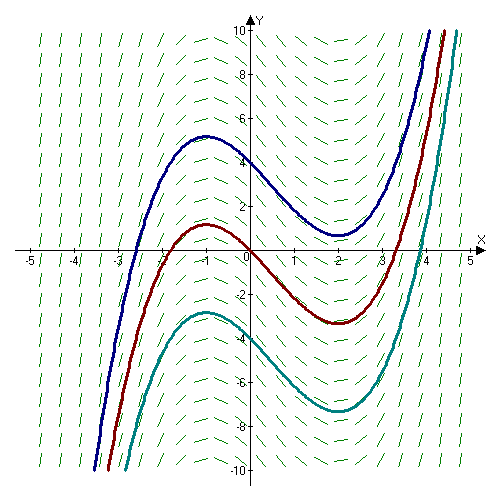
Indefinite Integral
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, velocity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Derivatives And Integrals In Alternative Calculi
There are many alternatives to the classical calculus of Newton and Leibniz; for example, each of the infinitely many non-Newtonian calculi. Occasionally an alternative calculus is more suited than the classical calculus for expressing a given scientific or mathematical idea. The table below is intended to assist people working with the alternative calculus called the "geometric calculus" (or its discrete analog). Interested readers are encouraged to improve the table by inserting citations for verification, and by inserting more functions and more calculi. Table In the following table; \psi(x)=\frac is the digamma function, \operatorname(x)=e^=e^ is the K-function, (!x)=\frac is subfactorial, B_a(x)=-a\zeta(-a+1,x) are the generalized to real numbers Bernoulli polynomials. See also *Derivative *Differentiation rules *Indefinite product * Product integral *Fractal derivative In applied mathematics and mathematical analysis, the fractal derivative or Hausdorf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Difference
A finite difference is a mathematical expression of the form . Finite differences (or the associated difference quotients) are often used as approximations of derivatives, such as in numerical differentiation. The difference operator, commonly denoted \Delta, is the operator (mathematics), operator that maps a function to the function \Delta[f] defined by \Delta[f](x) = f(x+1)-f(x). A difference equation is a functional equation that involves the finite difference operator in the same way as a differential equation involves derivatives. There are many similarities between difference equations and differential equations. Certain Recurrence relation#Relationship to difference equations narrowly defined, recurrence relations can be written as difference equations by replacing iteration notation with finite differences. In numerical analysis, finite differences are widely used for #Relation with derivatives, approximating derivatives, and the term "finite difference" is often used a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Function
In mathematics, physics and engineering, the sinc function ( ), denoted by , has two forms, normalized and unnormalized.. In mathematics, the historical unnormalized sinc function is defined for by \operatorname(x) = \frac. Alternatively, the unnormalized sinc function is often called the sampling function, indicated as Sa(''x''). In digital signal processing and information theory, the normalized sinc function is commonly defined for by \operatorname(x) = \frac. In either case, the value at is defined to be the limiting value \operatorname(0) := \lim_\frac = 1 for all real (the limit can be proven using the squeeze theorem). The normalization causes the definite integral of the function over the real numbers to equal 1 (whereas the same integral of the unnormalized sinc function has a value of ). As a further useful property, the zeros of the normalized sinc function are the nonzero integer values of . The normalized sinc function is the Fourier transform of the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lerch Transcendent
In mathematics, the Lerch transcendent, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech mathematician Mathias Lerch, who published a paper about a similar function in 1887. The Lerch transcendent, is given by: :\Phi(z, s, \alpha) = \sum_^\infty \frac . It only converges for any real number \alpha > 0, where , z, 1, and , z, = 1. Special cases The Lerch transcendent is related to and generalizes various special functions. The Lerch zeta function is given by: :L(\lambda, s, \alpha) = \sum_^\infty \frac =\Phi(e^, s,\alpha) The Hurwitz zeta function is the special case :\zeta(s,\alpha) = \sum_^\infty \frac = \Phi(1,s,\alpha) The polylogarithm is another special case: :\textrm_s(z) = \sum_^\infty \frac =z\Phi(z,s,1) The Riemann zeta function is a special case of both of the above: :\zeta(s) =\sum_^\infty \frac = \Phi(1,s,1) The Dirichlet eta function: :\eta(s) = \sum_^\infty \frac = \Phi(-1,s,1) The Diric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Harmonic Number
In mathematics, the -th harmonic number is the sum of the reciprocals of the first natural numbers: H_n= 1+\frac+\frac+\cdots+\frac =\sum_^n \frac. Starting from , the sequence of harmonic numbers begins: 1, \frac, \frac, \frac, \frac, \dots Harmonic numbers are related to the harmonic mean in that the -th harmonic number is also times the reciprocal of the harmonic mean of the first positive integers. Harmonic numbers have been studied since antiquity and are important in various branches of number theory. They are sometimes loosely termed harmonic series, are closely related to the Riemann zeta function, and appear in the expressions of various special functions. The harmonic numbers roughly approximate the natural logarithm function and thus the associated harmonic series grows without limit, albeit slowly. In 1737, Leonhard Euler used the divergence of the harmonic series to provide a new proof of the infinity of prime numbers. His work was extended into the com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q-analog
In mathematics, a ''q''-analog of a theorem, identity or expression is a generalization involving a new parameter ''q'' that returns the original theorem, identity or expression in the limit as . Typically, mathematicians are interested in ''q''-analogs that arise naturally, rather than in arbitrarily contriving ''q''-analogs of known results. The earliest ''q''-analog studied in detail is the basic hypergeometric series, which was introduced in the 19th century. ''q''-analogs are most frequently studied in the mathematical fields of combinatorics and special functions. In these settings, the limit is often formal, as is often discrete-valued (for example, it may represent a prime power). ''q''-analogs find applications in a number of areas, including the study of fractals and multi-fractal measures, and expressions for the entropy of chaotic dynamical systems. The relationship to fractals and dynamical systems results from the fact that many fractal patterns have the symme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Product
In mathematics, the indefinite product operator is the inverse operator of Q(f(x)) = \frac. It is a discrete version of the geometric integral of geometric calculus, one of the non-Newtonian calculi. Thus :Q\left( \prod_x f(x) \right) = f(x) \, . More explicitly, if \prod_x f(x) = F(x) , then :\frac = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''CF''(''x'') for any constant ''C''. Therefore, each indefinite product actually represents a family of functions, differing by a multiplicative constant. Period rule If T is a period of function f(x) then :\prod _x f(Tx)=C f(Tx)^ Connection to indefinite sum Indefinite product can be expressed in terms of indefinite sum: :\prod _x f(x)= \exp \left(\sum _x \ln f(x)\right) Alternative usage Some authors use the phrase "indefinite product" in a slightly different but related way to describe a product in which the numerical value of the upper limit is not given. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incomplete Gamma Function
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals. Their respective names stem from their integral definitions, which are defined similarly to the gamma function but with different or "incomplete" integral limits. The gamma function is defined as an integral from zero to infinity. This contrasts with the lower incomplete gamma function, which is defined as an integral from zero to a variable upper limit. Similarly, the upper incomplete gamma function is defined as an integral from a variable lower limit to infinity. Definition The upper incomplete gamma function is defined as: \Gamma(s,x) = \int_x^ t^\,e^\, dt , whereas the lower incomplete gamma function is defined as: \gamma(s,x) = \int_0^x t^\,e^\, dt . In both cases is a complex parameter, such that the real part of is positive. Properties By integration by parts we find the recurrence relati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Super-exponential Function
In mathematics, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though Knuth's up arrow notation \uparrow \uparrow and the left-exponent ^b are common. Under the definition as repeated exponentiation, means , where ' copies of ' are iterated via exponentiation, right-to-left, i.e. the application of exponentiation n-1 times. ' is called the "height" of the function, while ' is called the "base," analogous to exponentiation. It would be read as "the th tetration of ". For example, 2 tetrated to 4 (or the fourth tetration of 2) is =2^=2^=2^=65536. It is the next hyperoperation after exponentiation, but before pentation. The word was coined by Reuben Louis Goodstein from tetra- (four) and iteration. Tetration is also defined recursively as : := \begin 1 &\textn=0, \\ a^ &\textn>0, \end allowing for the holomorphic extension of tetration to non-natural numbers such as real, complex, and ord ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |