|
XXVII Liceum Ogólnokształcące Im. Tadeusza Czackiego
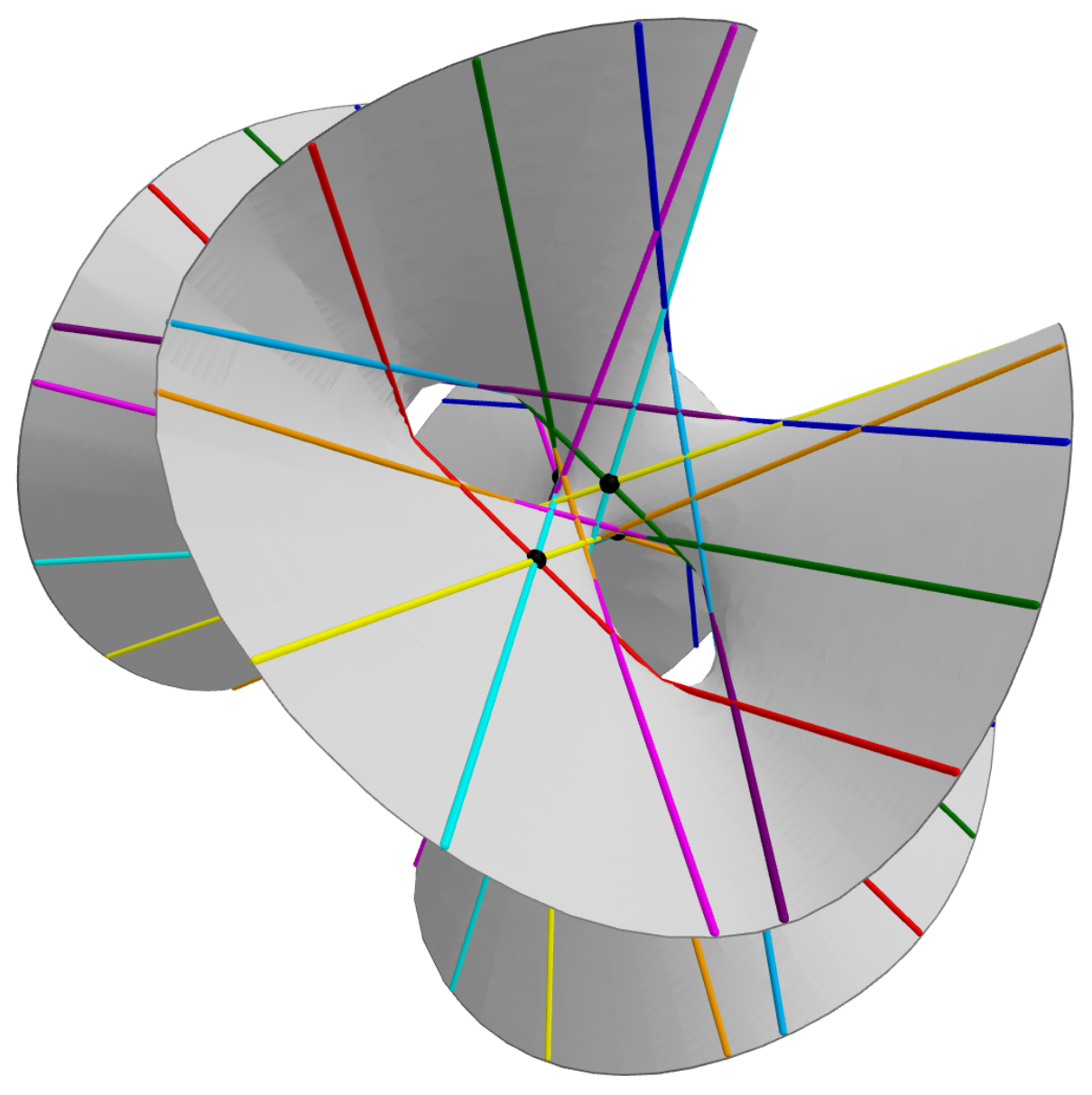
27 (twenty-seven) is the natural number following 26 and preceding 28. Mathematics Including the null-motif, there are 27 distinct hypergraph motifs. There are exactly ''twenty-seven straight lines'' on a smooth cubic surface, which give a basis of the fundamental representation of Lie algebra \mathrm . The unique simple formally real Jordan algebra, the exceptional Jordan algebra of self-adjoint 3 by 3 matrices of quaternions, is 27-dimensional; its automorphism group is the 52-dimensional exceptional Lie algebra \mathrm . There are twenty-seven sporadic groups, if the ''non-strict'' group of Lie type \mathrm (with an irreducible representation that is twice that of \mathrm in 104 dimensions) is included. In Robin's theorem for the Riemann hypothesis, twenty-seven integers fail to hold \sigma(n) < e^\gamma n \log \log n for values where is the |
26 (number)
26 (twenty-six) is the natural number following 25 and preceding 27. In mathematics *26 is the seventh discrete semiprime (2 \times 13) and the fifth with 2 as the lowest non-unitary factor thus of the form (2.q), where q is a higher prime. *26 is the smallest even number ''n'' such that both ''n'' + 1 and ''n'' − 1 are composite. *With an aliquot sum of 16, within an aliquot sequence of five composite numbers (26, 16, 15, 9, 4, 3, 1,0) to the Prime in the 3-aliquot tree. *26 is the only integer that is one greater than a square (5 + 1) and one less than a cube (3 − 1). *26 is a telephone number, specifically, the number of ways of connecting 5 points with pairwise connections. *There are 26 sporadic groups. *The 26-dimensional Lorentzian unimodular lattice II25,1 plays a significant role in sphere packing problems and the classification of finite simple groups. In particular, the Leech lattice is obtained in a simple way as a subquotient. *26 is the smallest numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automorphism Group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the group of invertible linear transformations from ''X'' to itself (the general linear group of ''X''). If instead ''X'' is a group, then its automorphism group \operatorname(X) is the group consisting of all group automorphisms of ''X''. Especially in geometric contexts, an automorphism group is also called a symmetry group. A subgroup of an automorphism group is sometimes called a transformation group. Automorphism groups are studied in a general way in the field of category theory. Examples If ''X'' is a set with no additional structure, then any bijection from ''X'' to itself is an automorphism, and hence the automorphism group of ''X'' in this case is precisely the symmetric group of ''X''. If the set ''X'' has additional structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clebsch Surface
In mathematics, the Clebsch diagonal cubic surface, or Klein's icosahedral cubic surface, is a non-singular cubic surface, studied by and , all of whose 27 exceptional lines can be defined over the real numbers. The term Klein's icosahedral surface can refer to either this surface or its blowing up, blowup at the 10 Eckardt points. Definition The Clebsch surface is the set of points (''x''0:''x''1:''x''2:''x''3:''x''4) of projective space, P4 satisfying the equations :x_0 + x_1 + x_2 + x_3 + x_4 = 0, :x_0^3 + x_1^3 + x_2^3 + x_3^3 + x_4^3 = 0. Eliminating ''x''0 shows that it is also isomorphic to the surface :x_1^3 + x_2^3 + x_3^3 + x_4^3 = (x_1 + x_2 + x_3 + x_4)^3 in P3. In , it can be represented by Properties The symmetry group of the Clebsch surface is the symmetric group ''S''5 of order 120, acting by permutations of the coordinates (in ''P''4). Up to isomorphism, the Clebsch surface is the only cubic surface with this automorphism group. The 27 exceptional lines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal De Mathématiques Pures Et Appliquées
The ''Journal de Mathématiques Pures et Appliquées'' () is a French monthly scientific journal of mathematics, founded in 1836 by Joseph Liouville (editor: 1836–1874). The journal was originally published by Charles Louis Étienne Bachelier. After Bachelier's death in 1853, publishing passed to his son-in-law, Louis Alexandre Joseph Mallet, and the journal was marked Mallet-Bachelier. The publisher was sold to Gauthier-Villars ( fr) in 1863, where it remained for many decades. The journal is currently published by Elsevier. According to the 2018 Journal Citation Reports, its impact factor is 2.464. Articles are written in English or French. References External links * Online access* http://sites.mathdoc.fr/JMPA/ Index of freely available volumes Up to 1945, volumes of Journal de Mathématiques Pures et Appliquées are available online free in their entirety from Internet Archive The Internet Archive is an American 501(c)(3) organization, non-profit organiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Ramanujan Journal
''The Ramanujan Journal'' is a peer-reviewed scientific journal covering all areas of mathematics, especially those influenced by the Indian mathematician Srinivasa Ramanujan. The journal was established in 1997 and is published by Springer Science+Business Media. According to the ''Journal Citation Reports'', the journal has a 2021 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 0.804. References External links * {{DEFAULTSORT:Ramanujan Journal, The English-language journals Mathematics journals Springer Science+Business Media academic journals Academic journals established in 1997 9 times per year journals Srinivasa Ramanujan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Mascheroni Constant
Euler's constant (sometimes called the Euler–Mascheroni constant) is a mathematical constant, usually denoted by the lowercase Greek letter gamma (), defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by : \begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,\mathrm dx. \end Here, represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43), where he described it as "worthy of serious consideration". Euler initially calculated the constant's value to 6 decimal places. In 1781, he calculated it to 16 decimal places. Euler used the notations and for the constant. The Italian mathematician Lorenzo Mascheroni attempted to calculate the constant to 32 dec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by , after whom it is named. The Riemann hypothesis and some of its generalizations, along with Goldbach's conjecture and the twin prime conjecture, make up Hilbert's eighth problem in David Hilbert's list of twenty-three unsolved problems; it is also one of the Millennium Prize Problems of the Clay Mathematics Institute, which offers US$1 million for a solution to any of them. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields. The Riemann zeta function ''ζ''(''s'') is a function whose argument ''s'' may be any complex numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robin's Theorem
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function ''σ''''z''(''n''), for a real or complex number ''z'', is defined as the sum of the ''z''th powers of the positive divisors of ''n''. It can be expressed in sigma notation as :\sigma_z(n)=\sum_ d^z\,\! , where is shorthand for "''d' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Calgary
{{Infobox university , name = University of Calgary , image = University of Calgary coat of arms without motto scroll.svg , image_size = 150px , caption = Coat of arms , former_name = Normal School (1905–1913)Calgary Normal School (1913–1945)Calgary Branch of the Faculty of Education of the University of Alberta (1945–1958)University of Alberta in Calgary (1958–1966){{efn, The following are names of the predecessor institution which the University of Calgary originates from, prior to its reorganization as a standalone university. , motto = {{Lang, gd, Mo Shùile Togam Suas (Canadian Gaelic, Gaelic) , mottoeng = I will lift up my eyes , established = {{Start date and age, 1966, 04, 26, df=yes, p=yes, br=yes , type = Public university, Public , endowment = {{CAD, 1.176 billion (2023) , chancellor = J ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faithful Representation
In mathematics, especially in an area of abstract algebra known as representation theory, a faithful representation ρ of a group (mathematics), group on a vector space is a linear representation in which different elements of are represented by distinct linear mappings . In more abstract language, this means that the group homomorphism \rho: G\to GL(V) is injective (or injective, one-to-one). Caveat While representations of over a field (mathematics), field are ''de facto'' the same as -module (mathematics), modules (with denoting the Group ring#Group algebra over a finite group, group algebra of the group ), a faithful representation of is not necessarily a faithful module for the group algebra. In fact each faithful -module is a faithful representation of , but the converse (logic), converse does not hold. Consider for example the natural representation of the symmetric group in dimensions by permutation matrices, which is certainly faithful. Here the order of a group, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tits Group
In group theory, the Tits group 2''F''4(2)′, named for Jacques Tits (), is a finite simple group of order : 17,971,200 = 211 · 33 · 52 · 13. This is the only simple group that is a derivative of a group of Lie type that is not a group of Lie type in any series from exceptional isomorphisms. It is sometimes considered a 27th sporadic group. History and properties The Ree groups 2''F''4(22''n''+1) were constructed by , who showed that they are simple if ''n'' ≥ 1. The first member 2''F''4(2) of this series is not simple. It was studied by who showed that it is almost simple, its derived subgroup 2''F''4(2)′ of index 2 being a new simple group, now called the Tits group. The group 2''F''4(2) is a group of Lie type and has a BN pair, but the Tits group itself does not have a BN pair. The Tits group is member of the infinite family 2''F''4(22''n''+1)′ of commutator groups of the Ree groups, and thus by def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |