|
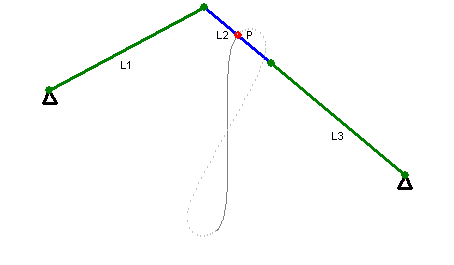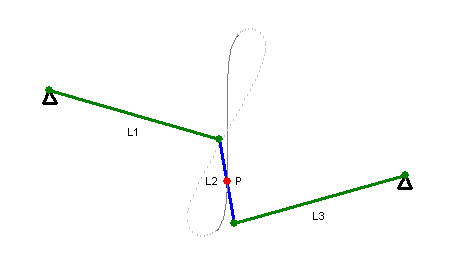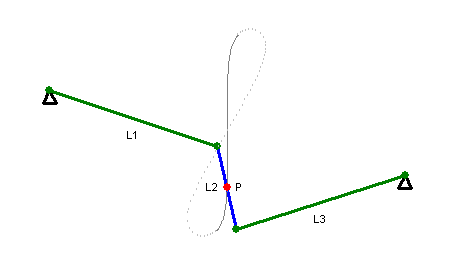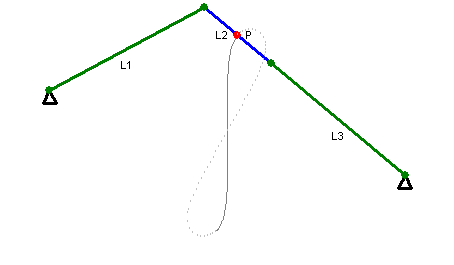
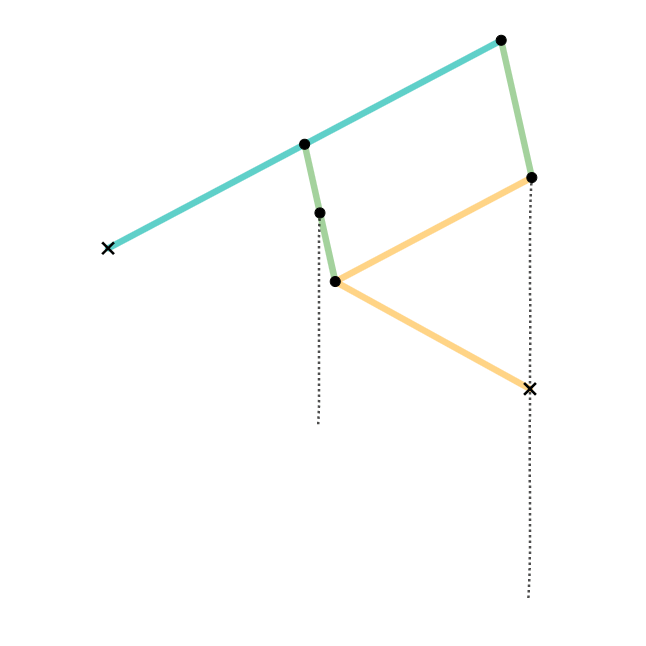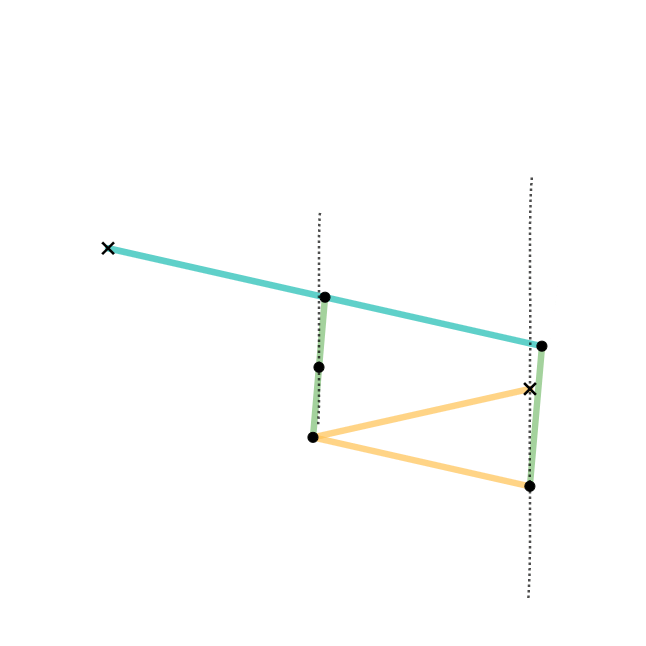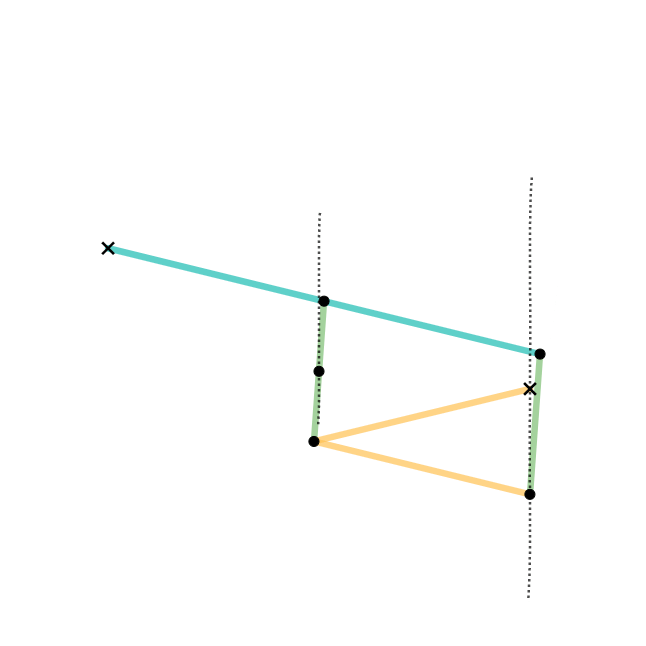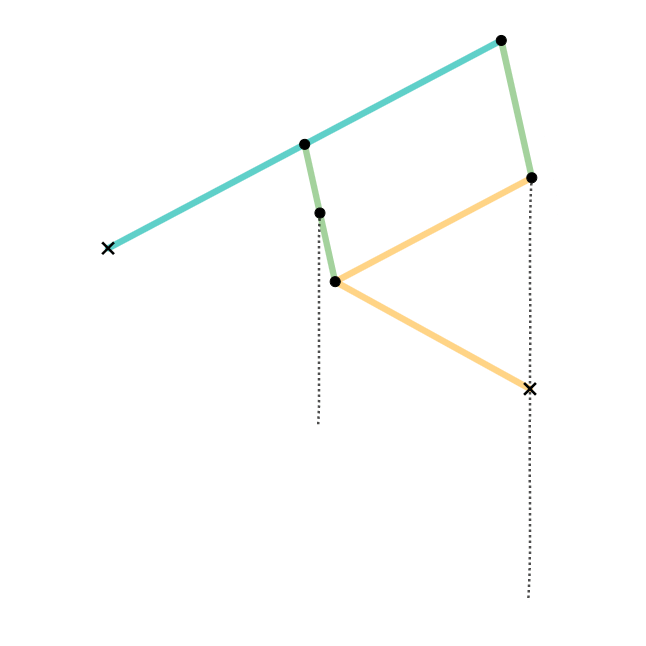
Watt's Curve
In mathematics, Watt's curve is a circular algebraic curve, tricircular algebraic curve, plane algebraic curve of sextic, degree six. It is generated by two circles of radius ''b'' with centers distance 2''a'' apart (taken to be at (±''a'', 0)). A line segment of length 2''c'' attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate partially back and forth or completely around. It arose in connection with James Watt's pioneering work on the steam engine. The equation of the curve can be given in polar coordinates as :r^2=b^2-\left[a\sin\theta\pm\sqrt\right]^2. Derivation Polar coordinates The polar equation for the curve can be derived as follows: Working in the complex plane, let the centers of the circles be at ''a'' and ''−a'', and the connecting segment have endpoints at ''−a''+''be''''i'' λ and ''a''+''be''''i'' ρ. Let the angle of inclination of the segment be ψ with its midpoint at ''re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hippopede
In geometry, a hippopede () is a plane curve determined by an equation of the form :(x^2+y^2)^2=cx^2+dy^2, where it is assumed that and since the remaining cases either reduce to a single point or can be put into the given form with a rotation. Hippopedes are circular algebraic curve, bicircular, Rational number, rational, algebraic curves of Degree of a polynomial, degree 4 and symmetric with respect to both the and axes. Special cases When ''d'' > 0 the curve has an oval form and is often known as an oval of Booth, and when the curve resembles a sideways figure eight, or lemniscate, and is often known as a lemniscate of Booth, after 19th-century mathematician James Booth (mathematician), James Booth who studied them. Hippopedes were also investigated by Proclus (for whom they are sometimes called Hippopedes of Proclus) and Eudoxus of Cnidus, Eudoxus. For , the hippopede corresponds to the lemniscate of Bernoulli. Definition as spiric sections Hippopedes can be defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathesis (journal)
''Mathesis: Recueil Mathématique'' was a Belgian scientific journal for elementary mathematics, established in 1881 by Paul Mansion and Joseph Jean Baptiste Neuberg Joseph Jean Baptiste Neuberg (30 October 1840 – 22 March 1926) was a Luxembourgish mathematician who worked primarily in geometry. Biography Neuberg was born on 30 October 1840 in Luxembourg City, Luxembourg. He first studied at a local sch .... An earlier Belgian mathematics journal, ''Nouvelle Correspondance Mathématique'', was established in 1874 by Mansion and Neuberg together with Eugène Catalan. In 1880, ''Nouvelle Correspondance'' ceased publication, and Mansion and Neuberg together launched its successor, ''Mathesis'', in 1881. ''Mathesis'' ceased publication in 1915 because of the war in Europe, but restarted again under the editorship of Neuberg and Adolphe Mineur in 1922 as the official journal of the Belgian Mathematical Society, which itself was founded in 1921. It continued in publication u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Watt's Linkage
A Watt's linkage is a type of mechanical linkage invented by James Watt in which the central moving point of the linkage is constrained to travel a nearly straight path. Watt's described the linkage in his patent specification of 1784 for the Watt steam engine. Today it is used in automobile suspensions, where it is key to a suspension's kinematics, i.e., its motion properties, constraining the vehicle axle's movement to nearly vertical travel while also limiting horizontal motion. Description Watt's linkage consists of three bars bolted together in a chain. The chain of bars consists of two end bars and a middle bar. The middle bar is bolted at each of its ends to one of the ends of each outer bar. The two outer bars are of equal length, and are longer than the middle bar. The three bars can pivot around the two bolts. The outer endpoints of the long bars are fixed in place relative to each other, but otherwise the three bars are free to pivot around the two joints where t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-bar Linkage
In the study of Mechanism (engineering), mechanisms, a four-bar linkage, also called a four-bar, is the simplest closed-Kinematic chain, chain movable linkage (mechanical), linkage. It consists of four Rigid body, bodies, called ''bars'' or ''links'', connected in a loop by four Kinematic pair, joints. Generally, the joints are configured so the links move in parallel planes, and the assembly is called a ''planar four-bar linkage''. Spherical and spatial four-bar linkages also exist and are used in practice. Planar four-bar linkage Planar four-bar linkages are constructed from four links connected in a loop by four one-degrees of freedom (mechanics), degree-of-freedom joints. A joint may be either a revolute joint – also known as a pin joint or hinged joint – denoted by R, or a prismatic joint – also known as a sliding pair – denoted by P. A link that is fixed in place relative to the viewer is called a ''ground link.'' A link connecting to the ground by a revolute joint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees). The side opposite to the right angle is called the '' hypotenuse'' (side c in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: '' cathetus''). Side a may be identified as the side ''adjacent'' to angle B and ''opposite'' (or ''opposed to'') angle A, while side b is the side adjacent to angle A and opposite angle B. Every right triangle is half of a rectangle which has been divided along its diagonal. When the rectangle is a square, its right-triangular half is isosceles, with two congruent sides and two congruent angles. When the rectangle is not a square, its right-triangular half is scalene. Every triangle whose base is the diameter of a circle and whose apex lies on the circle is a right triangle, with the right angle at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides , and the hypotenuse , sometimes called the Pythagorean equation: :a^2 + b^2 = c^2 . The theorem is named for the Ancient Greece, Greek philosopher Pythagoras, born around 570 BC. The theorem has been Mathematical proof, proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both Geometry, geometric proofs and Algebra, algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Watts Linkage
A Watt's linkage is a type of mechanical linkage invented by James Watt in which the central moving point of the linkage is constrained to travel a nearly straight path. Watt's described the linkage in his patent specification of 1784 for the Watt steam engine. Today it is used in automobile suspensions, where it is key to a suspension's kinematics, i.e., its motion properties, constraining the vehicle axle's movement to nearly vertical travel while also limiting horizontal motion. Description Watt's linkage consists of three bars bolted together in a chain. The chain of bars consists of two end bars and a middle bar. The middle bar is bolted at each of its ends to one of the ends of each outer bar. The two outer bars are of equal length, and are longer than the middle bar. The three bars can pivot around the two bolts. The outer endpoints of the long bars are fixed in place relative to each other, but otherwise the three bars are free to pivot around the two joints where t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acnode
An acnode is an isolated point in the solution set of a polynomial equation in two real variables. Equivalent terms are isolated point and hermit point. For example the equation :f(x,y)=y^2+x^2-x^3=0 has an acnode at the origin, because it is equivalent to :y^2 = x^2 (x-1) and x^2(x-1) is non-negative only when x ≥ 1 or x = 0. Thus, over the ''real'' numbers the equation has no solutions for x < 1 except for (0, 0). In contrast, over the complex numbers the origin is not isolated since square roots of negative real numbers exist. In fact, the complex solution set of a polynomial equation in two complex variables can never have an isolated point. An acnode is a critical point, or singularity, of the defining polynomial function, in the sense that both partial derivatives and vanish. Furth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points and , known as foci, at distance from each other as the locus of points so that . The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from , which is Latin for "decorated with hanging ribbons". It is a special case of the Cassini oval and is a rational algebraic curve of degree 4. This lemniscate was first described in 1694 by Jakob Bernoulli as a modification of an ellipse, which is the locus of points for which the sum of the distances to each of two fixed ''focal points'' is a constant. A Cassini oval, by contrast, is the locus of points for which the ''product'' of these distances is constant. In the case where the curve passes through the point midway between the foci, the oval is a lemniscate of Bernoulli. This curve can be obtained as the inverse transform of a hyperbola, with the inversion circle centered at the center of the hyperbola (bisect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertical Tangent
In mathematics, particularly calculus, a vertical tangent is a tangent, tangent line that is Vertical direction, vertical. Because a vertical line has Infinity, infinite slope, a Function (mathematics), function whose graph of a function, graph has a vertical tangent is not Differentiable function, differentiable at the point of tangency. Limit definition A function ƒ has a vertical tangent at ''x'' = ''a'' if the difference quotient used to define the derivative has Limit_of_a_function#Infinite_limits, infinite limit: :\lim_\frac = \quad\text\quad\lim_\frac = . The graph of ƒ has a vertical tangent at ''x'' = ''a'' if the derivative of ƒ at ''a'' is either positive or negative infinity. For a continuous function, it is often possible to detect a vertical tangent by taking the limit of the derivative. If :\lim_ f'(x) = \text then ƒ must have an upward-sloping vertical tangent at ''x'' = ''a''. Similarly, if :\lim_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |