|
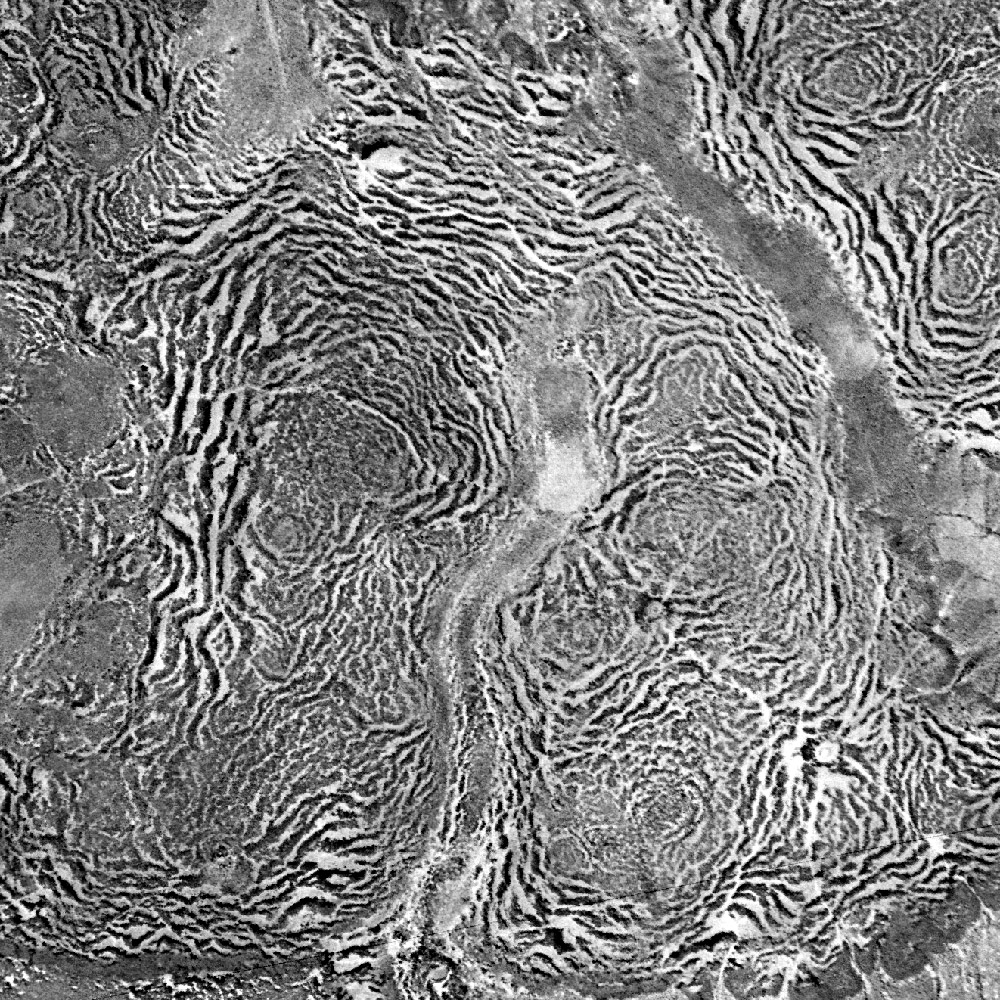
Turing Reaction-diffusion System
The Turing pattern is a concept introduced by English mathematician Alan Turing in a 1952 paper titled "The Chemical Basis of Morphogenesis" which describes how patterns in nature, such as stripes and spots, can arise naturally and autonomously from a homogeneous, uniform state. The pattern arises due to Turing instability which in turn arises due to the interplay between differential diffusion (i.e., different values of diffusion coefficients) of chemical species and chemical reaction. The instability mechanism is unforeseen because a pure diffusion process would be anticipated to have a stabilizing influence on the system. Overview In his paper, Turing examined the behaviour of a system in which two diffusible substances interact with each other, and found that such a system is able to generate a spatially periodic pattern even from a random or almost uniform initial condition. Prior to the discovery of this instability mechanism arising due to unequal diffusion coefficien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusive–thermal Instability
Diffusive–thermal instability or thermo–diffusive instability is an instrinsic flame instability that occurs both in premixed flames and in diffusion flames and arises because of the difference in the diffusion coefficient values for the fuel and heat transport, characterized by non-unity values of Lewis numbers. The instability mechanism that arises here is the same as in Turing instability explaining chemical morphogenesis, although the mechanism was first discovered in the context of combustion by Yakov Zeldovich in 1944 to explain the cellular structures appearing in lean hydrogen flames. Quantitative stability theory for premixed flames were developed by Gregory Sivashinsky (1977), Guy Joulin and Paul Clavin (1979) and for diffusion flames by Jong S. Kim (1997). Dispersion relation for premixed flames To neglect the influences by hydrodynamic instabilities such as Darrieus–Landau instability, Rayleigh–Taylor instability etc., the analysis usually neglects effects due ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liquid Crystals
Liquid crystal (LC) is a state of matter whose properties are between those of conventional liquids and those of solid crystals. For example, a liquid crystal may flow like a liquid, but its molecules may be oriented in a crystal-like way. There are many types of LC phases, which can be distinguished by their optical properties (such as textures). The contrasting textures arise due to molecules within one area of material ("domain") being oriented in the same direction but different areas having different orientations. LC materials may not always be in a LC state of matter (just as water may be ice or water vapor). Liquid crystals can be divided into 3 main types: *thermotropic, *lyotropic, and * metallotropic. Thermotropic and lyotropic liquid crystals consist mostly of organic molecules, although a few minerals are also known. Thermotropic LCs exhibit a phase transition into the LC phase as temperature changes. Lyotropic LCs exhibit phase transitions as a function of both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissipative Soliton
Dissipative solitons (DSs) are stable solitary localized structures that arise in nonlinear spatially extended dissipative systems due to mechanisms of self-organization. They can be considered as an extension of the classical soliton concept in conservative systems. An alternative terminology includes autosolitons, spots and pulses. Apart from aspects similar to the behavior of classical particles like the formation of bound states, DSs exhibit interesting behavior – e.g. scattering, creation and annihilation – all without the constraints of energy or momentum conservation. The excitation of internal degrees of freedom may result in a dynamically stabilized intrinsic speed, or periodic oscillations of the shape. Historical development Origin of the soliton concept DSs have been experimentally observed for a long time. Helmholtz measured the propagation velocity of nerve pulses in 1850. In 1902, Lehmann found the formation of localized anode spots in long gas-disc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stripe (pattern)
A stripe is a line or band that differs in color or tone from an adjacent area. Stripes are a group of such lines. Usage and appearance As a pattern (more than one stripe together), stripes are commonly seen in nature, food, emblems, clothing, and elsewhere. Two-toned stripes inherently draw one's attention, and as such are used to signal hazards. They are used in road signs, barricade tape, and thresholds. In nature, as with the zebra, stripes may have developed through natural selection to produce motion dazzle. Stripes may give appeal to certain sweets like the candy cane. For hundreds of years, stripes have been used in clothing. Striped clothing has frequently had negative symbolism in Western cultures. Historian Michel Pastoureau explores the cultural history of these design decisions in the book, ''The Devil's Cloth.'' See also * Square tiling * Sussi cloth *The Devil's Cloth * Argyle (pattern) * Racing flags * Flannel * Gingham * Madras (cloth) * Plaid ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spiral
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. Helices Two major definitions of "spiral" in the American Heritage Dictionary are:Spiral ''American Heritage Dictionary of the English Language'', Houghton Mifflin Company, Fourth Edition, 2009. # a curve on a plane that winds around a fixed center point at a continuously increasing or decreasing distance from the point. # a three-dimensional curve that turns around an axis at a constant or continuously varying distance while moving parallel to the axis; a . The first definition describes a planar curve, that exten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A ''regular hexagon'' has Schläfli symbol and can also be constructed as a truncated equilateral triangle, t, which alternates two types of edges. A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has six rotational symmetries (''rotational symmetry of order six'') and six reflection symmetries (''six lines of symmetry''), making up the dihedral group D6. The longest diagonals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Front (physics)
In physics, a front can be understood as an interface between two different possible states (either stable or unstable) in a physical system. For example, a weather front is the interface between two different density masses of air, in combustion where the flame is the interface between burned and unburned material or in population dynamics Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems. History Population dynamics has traditionally been the dominant branch of mathematical biology, which has ... where the front is the interface between populated and unpopulated places. Fronts can be static or mobile depending on the conditions of the system, and the causes of the motion can be the variation of a free energy, where the most energetically favorable state invades the less favorable one, according to Pomeau or shape induced motion due to non-variation dynamics in the system, according to Alva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pattern Formation
The science of pattern formation deals with the visible, (statistically) orderly outcomes of self-organization and the common principles behind similar patterns in nature. In developmental biology, pattern formation refers to the generation of complex organizations of cell fates in space and time. The role of genes in pattern formation is an aspect of morphogenesis, the creation of diverse anatomies from similar genes, now being explored in the science of evolutionary developmental biology or evo-devo. The mechanisms involved are well seen in the anterior-posterior patterning of embryos from the model organism ''Drosophila melanogaster'' (a fruit fly), one of the first organisms to have its morphogenesis studied, and in the eyespots of butterflies, whose development is a variant of the standard (fruit fly) mechanism. Patterns in nature Examples of pattern formation can be found in biology, physics, and science, and can readily be simulated with computer graphics, as desc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also publishes Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Spo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Biology
Mathematical and theoretical biology, or biomathematics, is a branch of biology which employs theoretical analysis, mathematical models and abstractions of the living organisms to investigate the principles that govern the structure, development and behavior of the systems, as opposed to experimental biology which deals with the conduction of experiments to prove and validate the scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side. Theoretical biology focuses more on the development of theoretical principles for biology while mathematical biology focuses on the use of mathematical tools to study biological systems, even though the two terms are sometimes interchanged. Mathematical biology aims at the mathematical representation and modeling of biological processes, using techniques and tools of applied mathematics. It can be useful in both theoretical and pra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |