|
Technical Definition
A technical definition is a definition in technical communication describing or explaining technical terminology. Technical definitions are used to introduce the vocabulary which makes communication in a particular field succinct and unambiguous. For example, the ''iliac crest'' from medical terminology is the top ridge of the hip bone (see ). Types of technical definitions There are three main types of technical definitions.Johnson-Sheehan, R: ''Technical Communication Today'', pages 507-522. Pearson Longman, 2007 # Power definitions # Secondary definitions # Extended definitions Examples Aniline, a benzene ring with an amine group, is a versatile chemical used in many organic syntheses. The genus ''Helogale'' (dwarf mongooses) contains two species. Sentence definitions These definitions generally appear in three different places: within the text, in margin notes, or in a glossary. Regardless of position in the document, most sentence definitions follow the basic form of term, ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Technical Terminology
Jargon, or technical language, is the specialized terminology associated with a particular field or area of activity. Jargon is normally employed in a particular Context (language use), communicative context and may not be well understood outside that context. The context is usually a particular occupation (that is, a certain trade, profession, vernacular or academic field), but any ingroups and outgroups, ingroup can have jargon. The key characteristic that distinguishes jargon from the rest of a language is its specialized vocabulary, which includes terms and definitions of words that are unique to the context, and terms used in a narrower and more exact sense than when used in colloquial language. This can lead In-group and out-group, outgroups to misunderstand communication attempts. Jargon is sometimes understood as a form of technical slang and then distinguished from the official terminology used in a particular field of activity. The terms ''jargon'', ''slang,'' and ''argot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aniline
Aniline (From , meaning ' indigo shrub', and ''-ine'' indicating a derived substance) is an organic compound with the formula . Consisting of a phenyl group () attached to an amino group (), aniline is the simplest aromatic amine. It is an industrially significant commodity chemical, as well as a versatile starting material for fine chemical synthesis. Its main use is in the manufacture of precursors to polyurethane, dyes, and other industrial chemicals. Like most volatile amines, it has the odor of rotten fish. It ignites readily, burning with a smoky flame characteristic of aromatic compounds. It is toxic to humans. Relative to benzene, aniline is "electron-rich". It thus participates more rapidly in electrophilic aromatic substitution reactions. Likewise, it is also prone to oxidation: while freshly purified aniline is an almost colorless oil, exposure to air results in gradual darkening to yellow or red, due to the formation of strongly colored, oxidized impurities. Ani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helogale
''Helogale'' is a genus of the mongoose family (Herpestidae). It consists of two species and 12 subspecies In Taxonomy (biology), biological classification, subspecies (: subspecies) is a rank below species, used for populations that live in different areas and vary in size, shape, or other physical characteristics (Morphology (biology), morpholog ...: Extant Species The helogales are the smallest species of mongooses and both are endemic to Africa. The distribution of the Ethiopian dwarf mongoose is more tropical, and overlaps completely with that of the common dwarf mongoose, which is more widespread. Both are social diurnal species, and due to their small sizes they are vulnerable to predation. Both species live independently of open water. References * The Kingdon Field Guide to African Mammals, 1997, Jonathan Kingdon. * Anne Rasa: ''Mongoose Watch: A Family Observed'', 1985, John Murray. Mongooses Taxa named by John Edward Gray {{ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
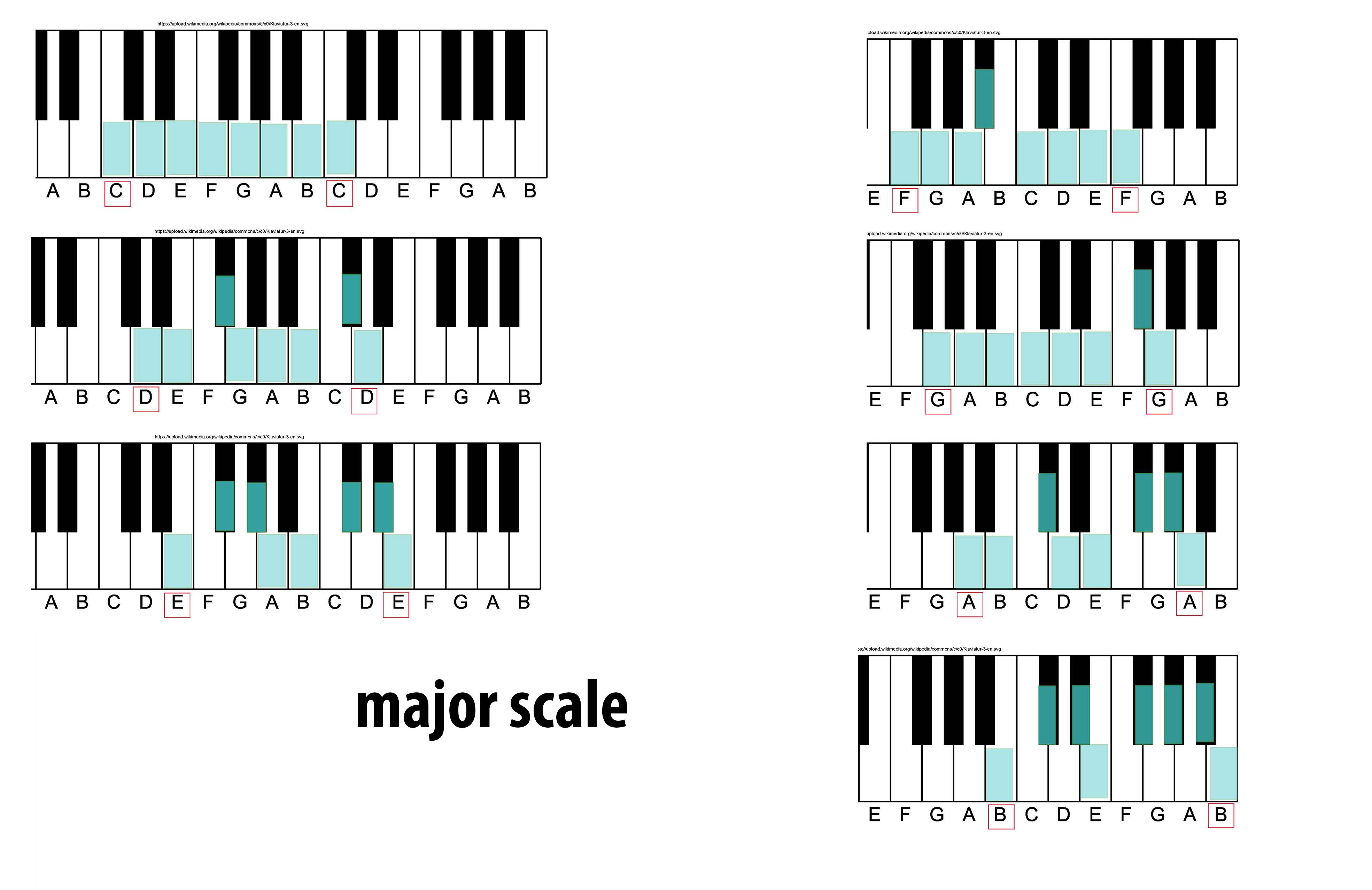
Major Scale
The major scale (or Ionian mode) is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double its frequency so that it is called a higher octave of the same note (from Latin "octavus", the eighth). The simplest major scale to write is C major, the only major scale not requiring sharps or flats: The major scale has a central importance in Western music, particularly that of the common practice period and in popular music. In Carnatic music, it is known as '' Sankarabharanam''. In Hindustani classical music, it is known as '' Bilaval''. Structure A major scale is a diatonic scale. The sequence of intervals between the notes of a major scale is: : whole, whole, half, whole, whole, whole, half where "whole" stands for a whole tone (a red u-shaped curve in the figure), and "half" stands for a semitone (a red angled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Scale
In music theory a diatonic scale is a heptatonic scale, heptatonic (seven-note) scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps. In other words, the half steps are maximally separated from each other. The seven pitch (music), pitches of any diatonic scale can also be obtained by using a Interval cycle, chain of six perfect fifths. For instance, the seven natural (music), natural pitch classes that form the C-major scale can be obtained from a stack of perfect fifths starting from F: :F–C–G–D–A–E–B. Any sequence of seven successive natural notes, such as C–D–E–F–G–A–B, and any Transposition (music), transposition thereof, is a diatonic scale. Modern musical keyboards are designed so that the white-key notes form a diatonic scale, though transpositions of this diatonic scale require one or more black keys. A diaton ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semitone
A semitone, also called a minor second, half step, or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale (or half of a whole step), visually seen on a keyboard as the distance between two keys that are adjacent to each other. For example, C is adjacent to C; the interval between them is a semitone. In a 12-note approximately equally divided scale, any interval can be defined in terms of an appropriate number of semitones (e.g. a whole tone or major second is 2 semitones wide, a major third 4 semitones, and a perfect fifth 7 semitones). In music theory, a distinction is made between a diatonic semitone, or minor second (an interval encompassing two different staff positions, e.g. from C to D) and a chromatic semitone or augmented unison (an interval between two notes at the same staff position, e.g. f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after the Norwegian mathematician Niels Henrik Abel. The concept of an abelian group underlies many fundamental algebraic structures, such as fields, rings, vector spaces, and algebras. The theory of abelian groups is generally simpler than that of their non-abelian counterparts, and finite abelian groups are very well understood and fully classified. Definition An abelian group is a set A, together with an operation ・ , that combines any two elements a and b of A to form another element of A, denoted a \cdot b. The sym ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantifier (logic)
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier \forall in the first-order formula \forall x P(x) expresses that everything in the domain satisfies the property denoted by P. On the other hand, the existential quantifier \exists in the formula \exists x P(x) expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable. The most commonly used quantifiers are \forall and \exists. These quantifiers are standardly defined as duals; in classical logic: each can be defined in terms of the other using negation. They can also be used to define more complex quantifiers, as in the formula \neg \exists x P(x) which expresses that nothing has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |