|
Shape Parameter
In probability theory and statistics, a shape parameter (also known as form parameter) is a kind of numerical parameter of a parametric family of probability distributionsEveritt B.S. (2002) Cambridge Dictionary of Statistics. 2nd Edition. CUP. that is neither a location parameter nor a scale parameter (nor a function of these, such as a rate parameter). Such a parameter must affect the ''shape'' of a distribution rather than simply shifting it (as a location parameter does) or stretching/shrinking it (as a scale parameter does). For example, "peakedness" refers to how round the main peak is. Estimation Many estimators measure location or scale; however, estimators for shape parameters also exist. Most simply, they can be estimated in terms of the higher moments, using the method of moments, as in the ''skewness'' (3rd moment) or ''kurtosis'' (4th moment), if the higher moments are defined and finite. Estimators of shape often involve higher-order statistics (non-linear functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Distribution
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval , 1in terms of two positive parameters, denoted by ''alpha'' (''α'') and ''beta'' (''β''), that appear as exponents of the random variable and control the shape of the distribution. The beta distribution has been applied to model the behavior of random variables limited to intervals of finite length in a wide variety of disciplines. The beta distribution is a suitable model for the random behavior of percentages and proportions. In Bayesian inference, the beta distribution is the conjugate prior probability distribution for the Bernoulli, binomial, negative binomial and geometric distributions. The formulation of the beta distribution discussed here is also known as the beta distribution of the first kind, whereas ''beta distribution of the second kind'' is an alternative name for the beta prime distribution. The generalization to mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto ( ), is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The Pareto principle or "80-20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value () of log45 ≈ 1.16 precisely reflect it. Empirical observation has shown that this 80-20 distribution fits a wide range of cases, including natural phenomena and human activities. Definitions If ''X'' is a random variable with a Pareto (Type I) distribution, then the probability that ''X'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Gaussian Distribution
In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,∞). Its probability density function is given by : f(x;\mu,\lambda) = \sqrt\frac \exp\biggl(-\frac\biggr) for ''x'' > 0, where \mu > 0 is the mean and \lambda > 0 is the shape parameter. The inverse Gaussian distribution has several properties analogous to a Gaussian distribution. The name can be misleading: it is an "inverse" only in that, while the Gaussian describes a Brownian motion's level at a fixed time, the inverse Gaussian describes the distribution of the time a Brownian motion with positive drift takes to reach a fixed positive level. Its cumulant generating function (logarithm of the characteristic function) is the inverse of the cumulant generating function of a Gaussian random variable. To indicate that a random variable ''X'' is inverse Gaussian-distributed with mean μ and sha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse-gamma Distribution
In probability theory and statistics, the inverse gamma distribution is a two-parameter family of continuous probability distributions on the positive real line, which is the distribution of the reciprocal of a variable distributed according to the gamma distribution. Perhaps the chief use of the inverse gamma distribution is in Bayesian statistics, where the distribution arises as the marginal posterior distribution for the unknown variance of a normal distribution, if an uninformative prior is used, and as an analytically tractable conjugate prior, if an informative prior is required. It is common among some Bayesians to consider an alternative parametrization of the normal distribution in terms of the precision, defined as the reciprocal of the variance, which allows the gamma distribution to be used directly as a conjugate prior. Other Bayesians prefer to parametrize the inverse gamma distribution differently, as a scaled inverse chi-squared distribution. Characterizatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-t Distribution
In probability theory, a log-t distribution or log-Student t distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Student's t-distribution. If ''X'' is a random variable with a Student's t-distribution, then ''Y'' = exp(''X'') has a log-t distribution; likewise, if ''Y'' has a log-t distribution, then ''X'' = log(''Y'') has a Student's t-distribution. Characterization The log-t distribution has the probability density function: :p(x\mid \nu,\hat,\hat) = \frac \left(1+\frac\left( \frac \right)^2\right)^ , where \hat is the location parameter of the underlying (non-standardized) Student's t-distribution, \hat is the scale parameter of the underlying (non-standardized) Student's t-distribution, and \nu is the number of degrees of freedom of the underlying Student's t-distribution. If \hat=0 and \hat=1 then the underlying distribution is the standardized Student's t-distribution. If \nu=1 then the distribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-logistic Distribution
In probability and statistics, the log-logistic distribution (known as the Fisk distribution in economics) is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, as, for example, mortality rate from cancer following diagnosis or treatment. It has also been used in hydrology to model stream flow and precipitation, in economics as a simple model of the distribution of wealth or income, and in networking to model the transmission times of data considering both the network and the software. The log-logistic distribution is the probability distribution of a random variable whose logarithm has a logistic distribution. It is similar in shape to the log-normal distribution but has heavier tails. Unlike the log-normal, its cumulative distribution function can be written in closed form. Characterization There are several different parameterizations of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Extreme Value Distribution
In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Note that a limit distribution needs to exist, which requires regularity conditions on the tail of the distribution. Despite this, the GEV distribution is often used as an approximation to model the maxima of long (finite) sequences of random variables. In some fields of application the generalized extreme value distribution is known as the Fisher–Tippett distribution, named after Ronald Fisher and L. H. C. Tippett who recognised three different forms outlined below. However usage of this name ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
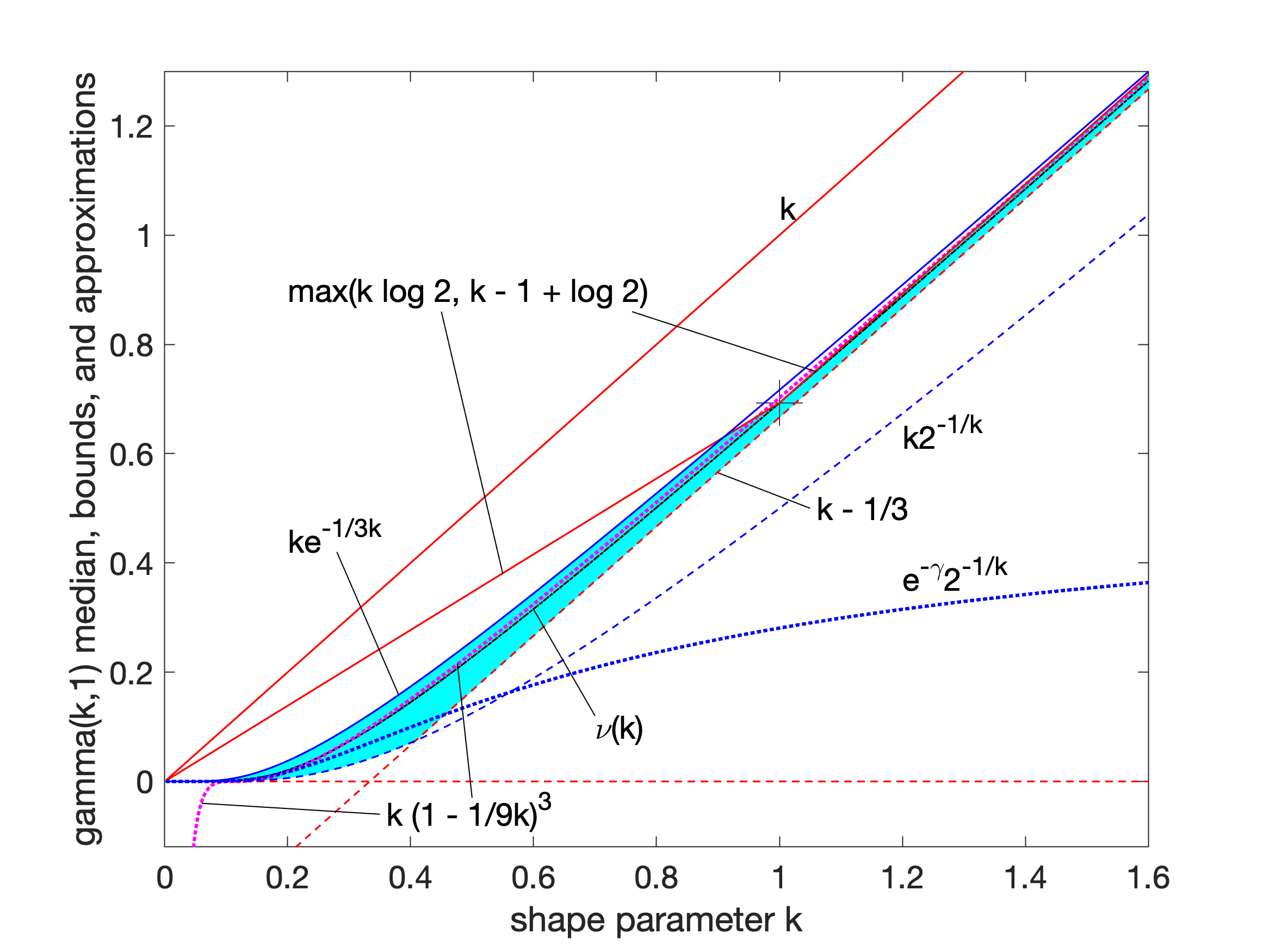
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common in econo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fréchet Distribution
The Fréchet distribution, also known as inverse Weibull distribution, is a special case of the generalized extreme value distribution. It has the cumulative distribution function :\Pr(X \le x)=e^ \text x>0. where ''α'' > 0 is a shape parameter. It can be generalised to include a location parameter ''m'' (the minimum) and a scale parameter ''s'' > 0 with the cumulative distribution function :\Pr(X \le x)=e^ \text x>m. Named for Maurice Fréchet who wrote a related paper in 1927, further work was done by Fisher–Tippett distribution, Fisher and Tippett in 1928 and by Emil Julius Gumbel, Gumbel in 1958. Characteristics The single parameter Fréchet with parameter \alpha has standardized moment :\mu_k=\int_0^\infty x^k f(x)dx=\int_0^\infty t^e^ \, dt, (with t=x^) defined only for k1 the Expected value, expectation is E[X]=\Gamma(1-\tfrac) * For \alpha>2 the variance is \text(X)=\Gamma(1-\tfrac)-\big(\Gamma(1-\tfrac)\big)^2. The quantile q_y of order y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Power Distribution
The generalized normal distribution or generalized Gaussian distribution (GGD) is either of two families of parametric continuous probability distributions on the real line. Both families add a shape parameter to the normal distribution. To distinguish the two families, they are referred to below as "symmetric" and "asymmetric"; however, this is not a standard nomenclature. Symmetric version The symmetric generalized normal distribution, also known as the exponential power distribution or the generalized error distribution, is a parametric family of Symmetric probability distribution, symmetric distributions. It includes all normal distribution, normal and Laplace distribution, Laplace distributions, and as limiting cases it includes all continuous uniform distributions on bounded intervals of the real line. This family includes the normal distribution when \textstyle\beta=2 (with mean \textstyle\mu and variance \textstyle \frac) and it includes the Laplace distribution whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ExGaussian Distribution
In probability theory, an exponentially modified Gaussian distribution (EMG, also known as exGaussian distribution) describes the sum of independent normal and exponential random variables. An exGaussian random variable ''Z'' may be expressed as , where ''X'' and ''Y'' are independent, ''X'' is Gaussian with mean ''μ'' and variance ''σ''2, and ''Y'' is exponential of rate ''λ''. It has a characteristic positive skew from the exponential component. It may also be regarded as a weighted function of a shifted exponential with the weight being a function of the normal distribution. Definition The probability density function (pdf) of the exponentially modified normal distribution is :f(x;\mu,\sigma,\lambda) = \frac e^ \operatorname \left(\frac\right), where erfc is the complementary error function defined as :\begin \operatorname(x) & = 1-\operatorname(x) \\ & = \frac \int_x^\infty e^\,dt. \end This density ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |