|
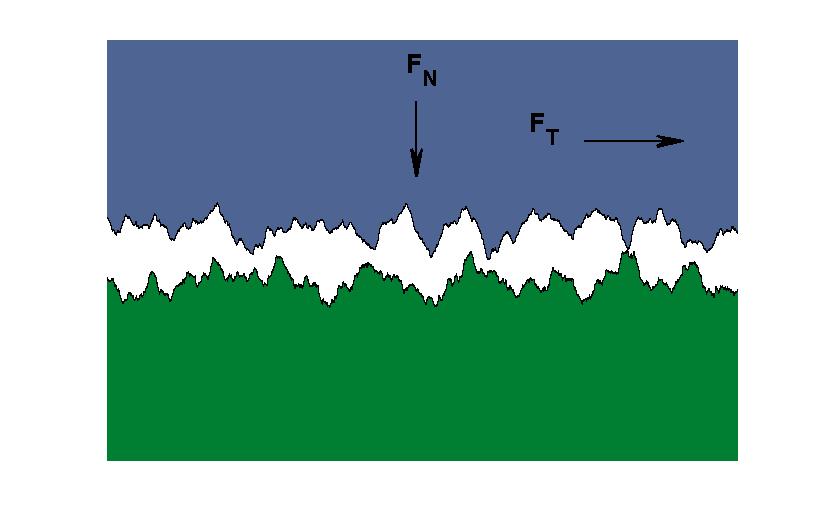
Surface Roughness
Surface roughness or simply roughness is the quality of a surface of not being smooth and it is hence linked to human ( haptic) perception of the surface texture. From a mathematical perspective it is related to the spatial variability structure of surfaces, and inherently it is a multiscale property. It has different interpretations and definitions depending on the disciplines considered. In surface metrology, surface roughness is a component of surface finish (surface texture). It is quantified by the deviations in the direction of the normal vector of a real surface from its ideal form. If these deviations are large, the surface is rough; if they are small, the surface is smooth. Roughness is typically assumed to be the high-frequency, short-wavelength component of a measured surface. However, in practice it is often necessary to know both the amplitude and frequency to ensure that a surface is fit for a purpose. Role and effect Roughness plays an important role in determin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Normal Contact Stiffness
Normal contact stiffness is a physical quantity related to the generalized force displacement behavior of rough surfaces in contact with a rigid body or a second similar rough surface. Specifically it is the amount of force per unit displacement required to compress an elastic object in the contact region. Rough surfaces can be considered as consisting of large numbers of asperities. As two solid bodies of the same material approach one another, the asperities interact, and they transition from conditions of non-contact to homogeneous bulk behaviour, with changes in the contact area. The varying values of stiffness and true contact area at an interface during this transition are dependent on the conditions of applied pressure and are of importance for the study of systems involving the physical interactions of multiple bodies including granular matter, electrode contacts, and thermal contact In heat transfer and thermodynamics, a thermodynamic system A thermodynamic system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Surface Roughness Skew2
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of Visual perception, sight and Somatosensory system, touch, and is the portion with which other materials first interact. The surface of an object is more than "a mere geometric solid", but is "filled with, spread over by, or suffused with perceivable qualities such as color and warmth". The concept of surface has been abstracted and formalized in mathematics, specifically in geometry. Depending on the properties on which the emphasis is given, there are several inequivalent such formalizations that are all called ''surface'', sometimes with a qualifier such as algebraic surface, smooth surface or fractal surface. The concept of surface and its mathematical abstractions are both widely used in physics, engineering, computer graphics, and many other disciplines, pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Abbott-Firestone Curve
The Abbott-Firestone curve or bearing area curve (BAC) describes the surface texture of an object. The curve can be found from a profile trace by drawing lines parallel to the datum and measuring the fraction of the line which lies within the profile. Mathematically it is the cumulative probability density function of the surface profile's height and can be calculated by integrating the probability density function. The Abbott-Firestone curve was first described by Ernest James Abbott and Floyd Firestone in 1933. It is useful for understanding the properties of sealing and bearing surfaces. It is commonly used in the engineering and manufacturing of piston cylinder bores of internal combustion engines. The shape of the curve is distilled into several of the surface roughness Surface roughness or simply roughness is the quality of a surface of not being smooth and it is hence linked to human ( haptic) perception of the surface texture. From a mathematical perspective it is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Savitzky–Golay Filter
A Savitzky–Golay filter is a digital filter that can be applied to a set of digital data points for the purpose of smoothing the data, that is, to increase the precision of the data without distorting the signal tendency. This is achieved, in a process known as convolution, by fitting successive sub-sets of adjacent data points with a low-degree polynomial by the method of linear least squares. When the data points are equally spaced, an analytical solution to the least-squares equations can be found, in the form of a single set of "convolution coefficients" that can be applied to all data sub-sets, to give estimates of the smoothed signal, (or derivatives of the smoothed signal) at the central point of each sub-set. The method, based on established mathematical procedures,. "Graduation Formulae obtained by fitting a Polynomial." was popularized by Abraham Savitzky and Marcel J. E. Golay, who published tables of convolution coefficients for various polynomials and sub-set sizes i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lathe
A lathe () is a machine tool that rotates a workpiece about an axis of rotation to perform various operations such as cutting, sanding, knurling, drilling, deformation, facing, threading and turning, with tools that are applied to the workpiece to create an object with symmetry about that axis. Lathes are used in woodturning, metalworking, metal spinning, thermal spraying, reclamation, and glass-working. Lathes can be used to shape pottery, the best-known design being the Potter's wheel. Most suitably equipped metalworking lathes can also be used to produce most solids of revolution, plane surfaces and screw threads or helices. Ornamental lathes can produce three-dimensional solids of incredible complexity. The workpiece is usually held in place by either one or two ''centers'', at least one of which can typically be moved horizontally to accommodate varying workpiece lengths. Other work-holding methods include clamping the work about the axis of rotation using a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Turning
Turning is a machining process in which a cutting tool, typically a non-rotary tool bit, describes a helix toolpath by moving more or less linearly while the workpiece rotates. Usually the term "turning" is reserved for the generation of ''external'' surfaces by this cutting action, whereas this same essential cutting action when applied to ''internal'' surfaces (holes, of one kind or another) is called " boring". Thus the phrase "turning and boring" categorizes the larger family of processes known as lathing. The cutting of faces on the workpiece, whether with a turning or boring tool, is called "facing", and may be lumped into either category as a subset. Turning can be done manually, in a traditional form of lathe, which frequently requires continuous supervision by the operator, or by using an automated lathe which does not. Today the most common type of such automation is computer numerical control, better known as CNC. (CNC is also commonly used with many other type ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kurtosis
In probability theory and statistics, kurtosis (from , ''kyrtos'' or ''kurtos'', meaning "curved, arching") refers to the degree of “tailedness” in the probability distribution of a real-valued random variable. Similar to skewness, kurtosis provides insight into specific characteristics of a distribution. Various methods exist for quantifying kurtosis in theoretical distributions, and corresponding techniques allow estimation based on sample data from a population. It’s important to note that different measures of kurtosis can yield varying interpretations. The standard measure of a distribution's kurtosis, originating with Karl Pearson, is a scaled version of the fourth moment of the distribution. This number is related to the tails of the distribution, not its peak; hence, the sometimes-seen characterization of kurtosis as " peakedness" is incorrect. For this measure, higher kurtosis corresponds to greater extremity of deviations (or outliers), and not the configur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution (a distribution with a single peak), negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value in skewness means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Thus, the judgement on the symmetry of a given distribution by using only its skewness is risky; the distribution shape must be taken into account. Introduction Consider the two d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Root Mean Square
In mathematics, the root mean square (abbrev. RMS, or rms) of a set of values is the square root of the set's mean square. Given a set x_i, its RMS is denoted as either x_\mathrm or \mathrm_x. The RMS is also known as the quadratic mean (denoted M_2), a special case of the generalized mean. The RMS of a continuous function is denoted f_\mathrm and can be defined in terms of an integral of the square of the function. In estimation theory, the root-mean-square deviation of an estimator measures how far the estimator strays from the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform. In the case of a set of ''n'' values \, the RMS is : x_\text = \sqrt. The corresponding formula for a continuous function (or waveform) ''f''(''t'') defined over the interval T_1 \le t \le T_2 is : f_\text = \sqrt , and the R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Arithmetic Average
In mathematics and statistics, the arithmetic mean ( ), arithmetic average, or just the ''mean'' or ''average'' is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results from an experiment, an observational study, or a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics because it helps to distinguish it from other types of means, such as geometric and harmonic. Arithmetic means are also frequently used in economics, anthropology, history, and almost every other academic field to some extent. For example, per capita income is the arithmetic average of the income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic: it is greatly influenced by outliers (values much larger or smaller than most others). For skewed distributions, such as the distribution of income for which a few people's incomes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Range (statistics)
In descriptive statistics, the range of a set of data is size of the narrowest interval which contains all the data. It is calculated as the difference between the largest and smallest values (also known as the sample maximum and minimum). It is expressed in the same units as the data. The range provides an indication of statistical dispersion. Closely related alternative measures are the Interdecile range and the Interquartile range. Range of continuous IID random variables For ''n'' independent and identically distributed continuous random variables ''X''1, ''X''2, ..., ''X''''n'' with the cumulative distribution function G(''x'') and a probability density function g(''x''), let T denote the range of them, that is, T= max(''X''1, ''X''2, ..., ''X''''n'')- min(''X''1, ''X''2, ..., ''X''''n''). Distribution The range, T, has the cumulative distribution function ::F(t)= n \int_^\infty g(x) (x+t)-G(x) \, \textx. Gumbel notes that the "beauty of this formula is com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |