|
Support Vector Machines
In machine learning, support vector machines (SVMs, also support vector networks) are supervised max-margin models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories, SVMs are one of the most studied models, being based on statistical learning frameworks of VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). In addition to performing linear classification, SVMs can efficiently perform non-linear classification using the ''kernel trick'', representing the data only through a set of pairwise similarity comparisons between the original data points using a kernel function, which transforms them into coordinates in a higher-dimensional feature space. Thus, SVMs use the kernel trick to implicitly map their inputs into high-dimensional feature spaces, where linear classification can be performed. Being max-margin models, SVMs are resilient to noisy data (e.g., misclassified examples). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task (computing), tasks without explicit Machine code, instructions. Within a subdiscipline in machine learning, advances in the field of deep learning have allowed Neural network (machine learning), neural networks, a class of statistical algorithms, to surpass many previous machine learning approaches in performance. ML finds application in many fields, including natural language processing, computer vision, speech recognition, email filtering, agriculture, and medicine. The application of ML to business problems is known as predictive analytics. Statistics and mathematical optimisation (mathematical programming) methods comprise the foundations of machine learning. Data mining is a related field of study, focusing on exploratory data analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structured Prediction
Structured prediction or structured output learning is an umbrella term for supervised machine learning techniques that involves predicting structured objects, rather than discrete or real values. Similar to commonly used supervised learning techniques, structured prediction models are typically trained by means of observed data in which the predicted value is compared to the ground truth, and this is used to adjust the model parameters. Due to the complexity of the model and the interrelations of predicted variables, the processes of model training and inference are often computationally infeasible, so approximate inference and learning methods are used. Applications An example application is the problem of translating a natural language sentence into a syntactic representation such as a parse tree. This can be seen as a structured prediction problem in which the structured output domain is the set of all possible parse trees. Structured prediction is used in a wide variety ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Separability
In Euclidean geometry, linear separability is a property of two sets of points. This is most easily visualized in two dimensions (the Euclidean plane) by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are ''linearly separable'' if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if the line is replaced by a hyperplane. The problem of determining if a pair of sets is linearly separable and finding a separating hyperplane if they are, arises in several areas. In statistics and machine learning, classifying certain types of data is a problem for which good algorithms exist that are based on this concept. Mathematical definition Let X_ and X_ be two sets of points in an ''n''-dimensional Euclidean space. Then X_ and X_ are ''linearly separable'' if ther ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Machine
Kernel may refer to: Computing * Kernel (operating system), the central component of most operating systems * Kernel (image processing), a matrix used for image convolution * Compute kernel, in GPGPU programming * Kernel method, in machine learning * Kernelization, a technique for designing efficient algorithms ** Kernel, a routine that is executed in a vectorized loop, for example in general-purpose computing on graphics processing units * KERNAL, the Commodore operating system Mathematics Objects * Kernel (algebra), a general concept that includes: ** Kernel (linear algebra) or null space, a set of vectors mapped to the zero vector ** Kernel (category theory), a generalization of the kernel of a homomorphism ** Kernel (set theory), an equivalence relation: partition by image under a function ** Difference kernel, a binary equalizer: the kernel of the difference of two functions Functions * Kernel (geometry), the set of points within a polygon from which the whole polygo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
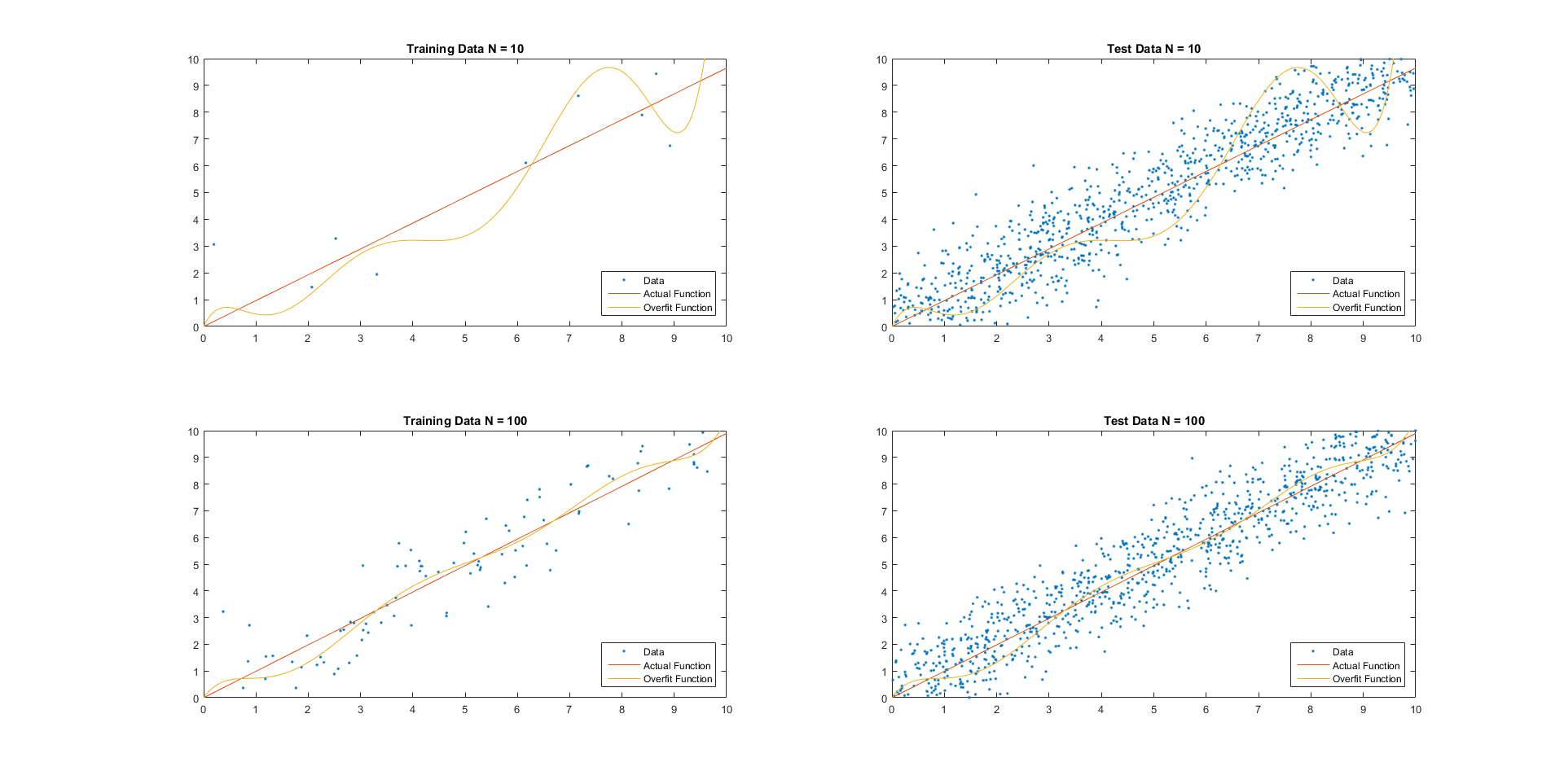
Overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfitted model is a mathematical model that contains more parameters than can be justified by the data. In the special case where the model consists of a polynomial function, these parameters represent the degree of a polynomial. The essence of overfitting is to have unknowingly extracted some of the residual variation (i.e., the Statistical noise, noise) as if that variation represented underlying model structure. Underfitting occurs when a mathematical model cannot adequately capture the underlying structure of the data. An under-fitted model is a model where some parameters or terms that would appear in a correctly specified model are missing. Underfitting would occur, for example, when fitting a linear model to nonlinear data. Such a model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalization Error
For supervised learning applications in machine learning and statistical learning theory, generalization errorMohri, M., Rostamizadeh A., Talwakar A., (2018) ''Foundations of Machine learning'', 2nd ed., Boston: MIT Press (also known as the out-of-sample errorY S. Abu-Mostafa, M.Magdon-Ismail, and H.-T. Lin (2012) Learning from Data, AMLBook Press. or the risk) is a measure of how accurately an algorithm is able to predict outcomes for previously unseen data. As learning algorithms are evaluated on finite samples, the evaluation of a learning algorithm may be sensitive to sampling error. As a result, measurements of prediction error on the current data may not provide much information about the algorithm's predictive ability on new, unseen data. The generalization error can be minimized by avoiding overfitting in the learning algorithm. The performance of machine learning algorithms is commonly visualized by Learning curve (machine learning), learning curve plots that show estimates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptron
In machine learning, the perceptron is an algorithm for supervised classification, supervised learning of binary classification, binary classifiers. A binary classifier is a function that can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of Weighting, weights with the feature vector. History The artificial neuron network was invented in 1943 by Warren McCulloch and Walter Pitts in ''A Logical Calculus of the Ideas Immanent in Nervous Activity, A logical calculus of the ideas immanent in nervous activity''. In 1957, Frank Rosenblatt was at the Cornell Aeronautical Laboratory. He simulated the perceptron on an IBM 704. Later, he obtained funding by the Information Systems Branch of the United States Office of Naval Research and the Rome Air Development Center, to build a custom- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margin Classifier
In machine learning (ML), a margin classifier is a type of classification model which is able to give an associated distance from the decision boundary for each data sample. For instance, if a linear classifier is used, the distance (typically Euclidean, though others may be used) of a sample from the separating hyperplane In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ... is the margin of that sample. The notion of ''margins'' is important in several ML classification algorithms, as it can be used to bound the generalization error of these classifiers. These bounds are frequently shown using the VC dimension. The generalization error bound in boosting algorithms and support vector machines is particularly prominent. Margin for boosting algorithms The margin for an iterative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum-margin Hyperplane
In geometry, the hyperplane separation theorem is a theorem about Disjoint sets, disjoint convex sets in ''n''-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are Closed set, closed and at least one of them is Compact set, compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal Projection (set theory), projections of the convex bodies onto the axis are disjoint. The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach theorem#Hahn–Banach separation theorem, Hahn–Banach separation theorem generalizes the result to topological vector spaces. A related result is the supporting hyperplane t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margin (machine Learning)
In machine learning, the margin of a single data point is defined to be the distance from the data point to a decision boundary. Note that there are many distances and decision boundaries that may be appropriate for certain datasets and goals. A margin classifier is a classification Classification is the activity of assigning objects to some pre-existing classes or categories. This is distinct from the task of establishing the classes themselves (for example through cluster analysis). Examples include diagnostic tests, identif ... model that utilizes the margin of each example to learn such classification. There are theoretical justifications (based on the VC dimension) as to why maximizing the margin (under some suitable constraints) may be beneficial for machine learning and statistical inference algorithms. For a given dataset, there may be many hyperplanes that could classify it. One reasonable choice as the best hyperplane is the one that represents the largest separatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is one less than that of the ambient space. Two lower-dimensional examples of hyperplanes are one-dimensional lines in a plane and zero-dimensional points on a line. Most commonly, the ambient space is -dimensional Euclidean space, in which case the hyperplanes are the -dimensional "flats", each of which separates the space into two half spaces. A reflection across a hyperplane is a kind of motion ( geometric transformation preserving distance between points), and the group of all motions is generated by the reflections. A convex polytope is the intersection of half-spaces. In non-Euclidean geometry, the ambient space might be the -dimensional sphere or hyperbolic space, or more generally a pseudo-Riemannian space form, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Point
In statistics, a unit of observation is the unit described by the data that one analyzes. A study may treat groups as a unit of observation with a country as the unit of analysis, drawing conclusions on group characteristics from data collected at the national level. For example, in a study of the demand for money, the unit of observation might be chosen as the individual, with different observations (data points) for a given point in time differing as to which individual they refer to; or the unit of observation might be the country, with different observations differing only in regard to the country they refer to. Unit of observation vs unit of analysis The unit of observation should not be confused with the unit of analysis. A study may have a differing unit of observation and unit of analysis: for example, in community research, the research design may collect data at the individual level of observation but the level of analysis might be at the neighborhood level, drawing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |