|
Square Pyramidal Number
In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid (geometry), pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes. As well as counting spheres in a pyramid, these numbers can be described algebraically as a sum of the first n positive square numbers, or as the values of a cubic polynomial. They can be used to solve several other counting problems, including counting squares in a square grid and counting acute triangles formed from the vertices of an odd regular polygon. They equal the sums of consecutive tetrahedral numbers, and are one-fourth of a larger tetrahedral number. The sum of two consecutive square pyramidal numbers is an octahedral number. History The pyramidal numbers were one of the few types of three-dimensional fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
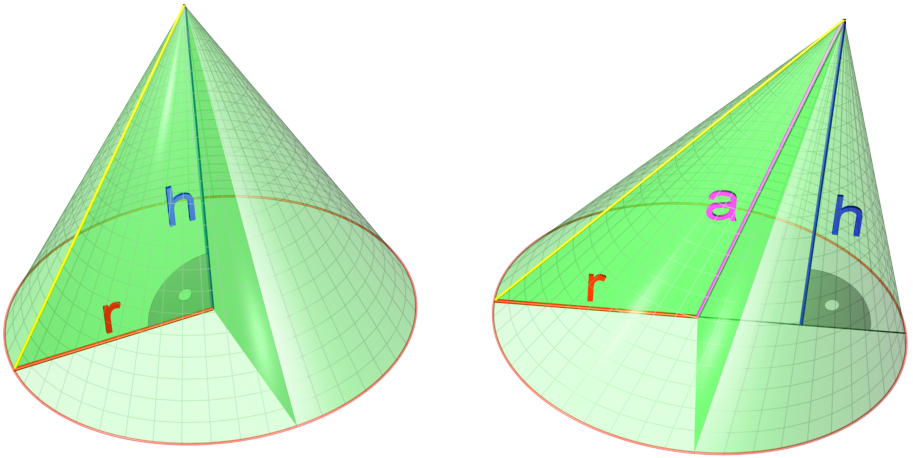
Cone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
55 (number)
55 (fifty-five) is the natural number following 54 (number), 54 and preceding 56 (number), 56. Mathematics 55 is: *the 10th Fibonacci number and the 10th triangular number, The sum of 55's digits is also 10. *the 5th heptagonal number, the 5th square pyramidal number, and the 4th centered nonagonal number. 55 is also the 19th semiprime and the 15th squarefree semiprime, as well as the 32nd Nontotient, nontotient number (including odd numbers > 1) the 36th arithmetic number, the 38th composite number (where the Abundant number, abundance of 55 = - 38), the 43rd deficient number, the 45th Polite number#Trapezoidal numbers, trapezoidal number, and the 49th polite number. Transportation *In the United States, the National Maximum Speed Law prohibited speed limits higher than from 1974 to 1987. The number ''55'' became a popular shorthand for the 55 mph speed limit. For example, a hand with a pair of fives in Texas hold'em poker is referred to as a "speed limit". Referenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
30 (number)
30 (thirty) is the natural number following 29 and preceding 31. In mathematics 30 is an even, composite, and pronic number. With 2, 3, and 5 as its prime factors, it is a regular number and the first sphenic number, the smallest of the form , where is a prime greater than 3. It has an aliquot sum of 42; within an aliquot sequence of thirteen composite numbers (30, 42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1, 0) to the Prime in the 3-aliquot tree. From 1 to the number 30, this is the longest Aliquot Sequence. It is also: * A semiperfect number, since adding some subsets of its divisors (e.g., 5, 10 and 15) equals 30. * A primorial. * A Harshad number in decimal. * Divisible by the number of prime numbers ( 10) below it. * The largest number such that all coprimes smaller than itself, except for 1, are prime. * The sum of the first four squares, making it a square pyramidal number. * The number of vertices in the Tutte–Coxeter graph. * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
14 (number)
14 (fourteen) is the natural number following 13 (number), 13 and preceding 15 (number), 15. Mathematics Fourteen is the seventh composite number. Properties 14 is the third distinct semiprime, being the third of the form 2 \times q (where q is a higher prime). More specifically, it is the first member of the second cluster of two discrete semiprimes (14, 15 (number), 15); the next such cluster is (21 (number), 21, 22 (number), 22), members whose sum is the fourteenth prime number, 43 (number), 43. 14 has an aliquot sum of 10 (number), 10, within an aliquot sequence of two composite numbers (14, 10 (number), 10, 8 (number), 8, 7 (number), 7, 1 (number), 1, 0) in the prime 7-aliquot tree. 14 is the third Pell number, companion Pell number and the fourth Catalan number. It is the lowest even n for which the Euler totient \varphi(x) = n has no solution, making it the first even nontotient. According to the Shapiro inequality, 14 is the least number n such that there exist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5 (number)
5 (five) is a number, numeral and digit. It is the natural number In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ..., and cardinal number, following 4 and preceding 6, and is a prime number. Humans, and many other animals, have 5 Digit (anatomy), digits on their Limb (anatomy), limbs. Mathematics 5 is a Fermat prime, a Mersenne prime exponent, as well as a Fibonacci number. 5 is the first congruent number, as well as the length of the hypotenuse of the smallest integer-sided right triangle, making part of the smallest Pythagorean triple (3, 4, 5). 5 is the first safe prime and the first good prime. 11 forms the first pair of sexy primes with 5. 5 is the second Fermat number, Fermat prime, of a total of five known Fermat primes. 5 is also the first of three known Wilso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1 (number)
1 (one, unit, unity) is a number, numeral, and glyph. It is the first and smallest positive integer of the infinite sequence of natural numbers. This fundamental property has led to its unique uses in other fields, ranging from science to sports, where it commonly denotes the first, leading, or top thing in a group. 1 is the unit of counting or measurement, a determiner for singular nouns, and a gender-neutral pronoun. Historically, the representation of 1 evolved from ancient Sumerian and Babylonian symbols to the modern Arabic numeral. In mathematics, 1 is the multiplicative identity, meaning that any number multiplied by 1 equals the same number. 1 is by convention not considered a prime number. In digital technology, 1 represents the "on" state in binary code, the foundation of computing. Philosophically, 1 symbolizes the ultimate reality or source of existence in various traditions. In mathematics The number 1 is the first natural number after 0. Each natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Édouard Lucas
__NOTOC__ François Édouard Anatole Lucas (; 4 April 1842 – 3 October 1891) was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him. Biography Lucas was born in Amiens and educated at the École Normale Supérieure. He worked in the Paris Observatory and later became a professor of mathematics at the Lycée Saint Louis and the Lycée Charlemagne in Paris. Lucas served as an artillery officer in the French Army during the Franco-Prussian War of 1870–1871. In 1875, Lucas posed a challenge to prove that the only solution of the Diophantine equation :\sum_^ n^2 = M^2\; with ''N'' > 1 is when ''N'' = 24 and ''M'' = 70. This is known as the cannonball problem, since it can be visualized as the problem of taking a square arrangement of cannonballs on the ground and building a square pyramid out of them. It was not until 1918 that a proof (using elliptic functions) was found for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cannonball Problem
In the mathematics of figurate numbers, the cannonball problem asks which numbers are both square and square pyramidal. The problem can be stated as: given a square arrangement of cannonballs, for what size squares can these cannonballs also be arranged into a square pyramid? Equivalently, which squares can be represented as the sum of consecutive squares, starting from 1? Formulation as a Diophantine equation When cannonballs are stacked within a square frame, the number of balls is a square pyramidal number; Thomas Harriot gave a formula for this number around 1587, answering a question posed to him by Sir Walter Raleigh Sir Walter Raleigh (; – 29 October 1618) was an English statesman, soldier, writer and explorer. One of the most notable figures of the Elizabethan era, he played a leading part in English colonisation of North America, suppressed rebell ... on their expedition to America. Édouard Lucas formulated the cannonball problem as a Diophantine equation : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Harriot
Thomas Harriot (; – 2 July 1621), also spelled Harriott, Hariot or Heriot, was an English astronomer, mathematician, ethnographer and translator to whom the theory of refraction is attributed. Thomas Harriot was also recognized for his contributions in navigational techniques, working closely with John White to create advanced maps for navigation. While Harriot worked extensively on numerous papers on the subjects of astronomy, mathematics and navigation, he remains obscure because he published little of it, namely only ''The Briefe and True Report of the New Found Land of Virginia'' (1588). This book includes descriptions of English settlements and financial issues in Virginia at the time. He is sometimes credited with the introduction of the potato to the British Isles. Harriot invented binary notation and arithmetic several decades before Gottfried Wilhelm Leibniz, but this remained unknown until the 1920s. He was also the first person to make a drawing of the Moon thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Walter Raleigh
Sir Walter Raleigh (; – 29 October 1618) was an English statesman, soldier, writer and explorer. One of the most notable figures of the Elizabethan era, he played a leading part in English colonisation of North America, suppressed rebellion in Ireland, helped defend England against the Spanish Armada and held political positions under Elizabeth I. Raleigh was born to a landed gentry family of Protestant faith in Devon, the son of Walter Raleigh and Catherine Champernowne. He was the younger half-brother of Sir Humphrey Gilbert and a cousin of Sir Richard Grenville. Little is known of his early life, though in his late teens he spent some time in France taking part in the religious civil wars. In his 20s he took part in the suppression of rebellion in the colonisation of Ireland; he also participated in the siege of Smerwick. Later, he became a landlord of property in Ireland and mayor of Youghal in east Munster, where his house still stands in Myrtle Grove. He rose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |