|
Sharaf Al-Dīn Al-Ṭūsī
Sharaf al-Dīn al-Muẓaffar ibn Muḥammad ibn al-Muẓaffar al-Ṭūsī (; Tus, Iran – Iran) known more often as Sharaf al-Dīn al-Ṭūsī or Sharaf ad-Dīn aṭ-Ṭūsī, was an Iranian mathematician and astronomer of the Islamic Golden Age (during the Middle Ages). Biography Al-Tusi was probably born in Tus, Iran. Little is known about his life, except what is found in the biographies of other scientists and that most mathematicians today can trace their lineage back to him. Around 1165, he moved to Damascus and taught mathematics there. He then lived in Aleppo for three years, before moving to Mosul, where he met his most famous disciple Kamal al-Din ibn Yunus (1156-1242). Kamal al-Din would later become the teacher of another famous mathematician from Tus, Nasir al-Din al-Tusi. According to Ibn Abi Usaibi'a, Sharaf al-Din was "outstanding in geometry and the mathematical sciences, having no equal in his time". Mathematics Al-Tusi has been credited with proposing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tus, Iran
Tus () was an ancient city in Khorasan near the modern city of Mashhad, Razavi Khorasan province, Iran. To the ancient Greeks, it was known as Susia (). It was also known as Tusa. The area now known as Tus was divided into four cities, Tabran, Radakan, Noan and Teroid, which in combination formed largest city in the region in the fifth century. History According to legend Tous son of Nowzar founded the city of Tous in the province of Khorassan next to today's city of Mashhad. It is said that the city of Tous was the capital of Parthia and the residence of King Vishtaspa, who was the first convert to Zoroastianism. It was captured by Alexander the Great in 330 BCE, and became a key waypoint on the Silk Road. Tus was taken by the Umayyad caliph Abd al-Malik and remained under Umayyad control until 747, when a subordinate of Abu Muslim Khorasani defeated the Umayyad governor during the Abbasid Revolution. In 809, the Abbasid Caliph Harun al-Rashid fell ill and died ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ruffini's Rule
In mathematics, Ruffini's rule is a method for computation of the Euclidean division of a polynomial by a binomial of the form ''x – r''. It was described by Paolo Ruffini in 1809. The rule is a special case of synthetic division in which the divisor is a linear factor. Algorithm The rule establishes a method for dividing the polynomial: :P(x)=a_nx^n+a_x^+\cdots+a_1x+a_0 by the binomial: :Q(x)=x-r to obtain the quotient polynomial: :R(x)=b_x^+b_x^+\cdots+b_1x+b_0. The algorithm is in fact the long division of ''P''(''x'') by ''Q''(''x''). To divide ''P''(''x'') by ''Q''(''x''): # Take the coefficients of ''P''(''x'') and write them down in order. Then, write ''r'' at the bottom-left edge just over the line: #: \begin & a_n & a_ & \dots & a_1 & a_0\\ r & & & & & \\ \hline & & & & & \\ \end # Pass the leftmost coefficient (''a''''n'') to the bottom just under the line. #: \begin & a_n & a_ & \dots & a_1 & a_0\\ r & & & & & \\ \hline & a_n & & & & \\ & =b_ & & & & \end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7058 Al-Ṭūsī
7 (seven) is the natural number following 6 and preceding 8. It is the only prime number preceding a cube. As an early prime number in the series of positive integers, the number seven has symbolic associations in religion, mythology, superstition and philosophy. The seven classical planets resulted in seven being the number of days in a week. 7 is often considered lucky in Western culture and is often seen as highly symbolic. Evolution of the Arabic digit For early Brahmi numerals, 7 was written more or less in one stroke as a curve that looks like an uppercase vertically inverted (ᒉ). The western Arab peoples' main contribution was to make the longer line diagonal rather than straight, though they showed some tendencies to making the digit more rectilinear. The eastern Arab peoples developed the digit from a form that looked something like 6 to one that looked like an uppercase V. Both modern Arab forms influenced the European form, a two-stroke form consisting of a ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Al-Andalus
Al-Andalus () was the Muslim-ruled area of the Iberian Peninsula. The name refers to the different Muslim states that controlled these territories at various times between 711 and 1492. At its greatest geographical extent, it occupied most of the peninsula as well as Septimania under Umayyad rule. These boundaries changed through a series of conquests Western historiography has traditionally characterized as the ''Reconquista'',"Para los autores árabes medievales, el término Al-Andalus designa la totalidad de las zonas conquistadas – siquiera temporalmente – por tropas arabo-musulmanas en territorios actualmente pertenecientes a Portugal, España y Francia" ("For medieval Arab authors, Al-Andalus designated all the conquered areas – even temporarily – by Arab-Muslim troops in territories now belonging to Spain, Portugal and France"), García de Cortázar, José Ángel. ''V Semana de Estudios Medievales: Nájera, 1 al 5 de agosto de 1994'', Gobie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrolabe
An astrolabe (; ; ) is an astronomy, astronomical list of astronomical instruments, instrument dating to ancient times. It serves as a star chart and Model#Physical model, physical model of the visible celestial sphere, half-dome of the sky. Its various functions also make it an elaborate inclinometer and an analog computer, analog calculation device capable of working out several kinds of problems in astronomy. In its simplest form it is a metal disc with a pattern of wires, cutouts, and perforations that allows a user to calculate astronomical positions precisely. It is able to measure the horizontal coordinate system, altitude above the horizon of a celestial body, day or night; it can be used to identify stars or planets, to determine local latitude given local time (and vice versa), to survey, or to triangulation, triangulate. It was used in classical antiquity, the Islamic Golden Age, the European Middle Ages and the Age of Discovery for all these purposes. The astrolabe, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Omar Khayyam
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīshābūrī (18 May 1048 – 4 December 1131) (Persian language, Persian: غیاث الدین ابوالفتح عمر بن ابراهیم خیام نیشابورﻯ), commonly known as Omar Khayyam (), was a Persian poet and polymath, known for his contributions to Mathematics in medieval Islam, mathematics, Astronomy in the medieval Islamic world, astronomy, Iranian philosophy, philosophy, and Persian literature. He was born in Nishapur, Iran and lived during the Seljuk Empire, Seljuk era, around the time of the First Crusade. As a mathematician, he is most notable for his work on the classification and solution of cubic equations, where he provided a geometric formulation based on the intersection of conics. He also contributed to a deeper understanding of Euclid's parallel axiom. As an astronomer, he calculated the duration of the solar year with remarkable precision and accuracy, and designed the Jalali calendar, a solar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects. The fundamental objects of study in algebraic geometry are algebraic variety, algebraic varieties, which are geometric manifestations of solution set, solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are line (geometry), lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscate of Bernoulli, lemniscates and Cassini ovals. These are plane algebraic curves. A point of the plane lies on an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of points of special interest like singular point of a curve, singular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roshdi Rashed
Roshdi Rashed (Arabic: رشدي راشد), born in Cairo in 1936, is a mathematician, philosopher and historian of science, whose work focuses largely on mathematics and physics of the medieval Arab world. His work explores and illuminates the unrecognized Arab scientific tradition, being one of the first historians to study in detail the ancient and medieval texts, their journey through the Eastern schools and courses, their immense contributions to Western science, particularly in regarding the development of algebra and the first formalization of physics. Biography Roshdi Rashed is the author of several books and scientific articles in History of Science. He is currently Emeritus Director of Research (special class) at CNRS (France). He was director of the Centre for History of Arab and Medieval Science and Philosophies (until 2001) Paris, and also director of the doctoral formation in epistemology and history of science, Paris Diderot University (until 2001). He is Emeritus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the zero of a function, roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factorization, polynomial factoring, number theory, and algebraic geometry. The discriminant of the quadratic polynomial ax^2+bx+c is :b^2-4ac, the quantity which appears under the square root in the quadratic formula. If a\ne 0, this discriminant is zero if and only if the polynomial has a double root. In the case of real number, real coefficients, it is positive if the polynomial has two distinct real roots, and negative if it has two distinct complex conjugate roots. Similarly, the discriminant of a cubic polynomial is zero if and only if the polynomial has a multiple root. In the case of a cubic with real coefficients, the discriminant is positive if the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxima And Minima
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative'' extrema) or on the entire domain (the ''global'' or ''absolute'' extrema) of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. In statistics, the corresponding concept is the sample maximum and minimum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient
In mathematics, a coefficient is a Factor (arithmetic), multiplicative factor involved in some Summand, term of a polynomial, a series (mathematics), series, or any other type of expression (mathematics), expression. It may be a Dimensionless quantity, number without units, in which case it is known as a numerical factor. It may also be a constant (mathematics), constant with units of measurement, in which it is known as a constant multiplier. In general, coefficients may be any mathematical expression, expression (including Variable (mathematics), variables such as , and ). When the combination of variables and constants is not necessarily involved in a product (mathematics), product, it may be called a ''parameter''. For example, the polynomial 2x^2-x+3 has coefficients 2, −1, and 3, and the powers of the variable x in the polynomial ax^2+bx+c have coefficient parameters a, b, and c. A , also known as constant term or simply constant, is a quantity either implicitly attach ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
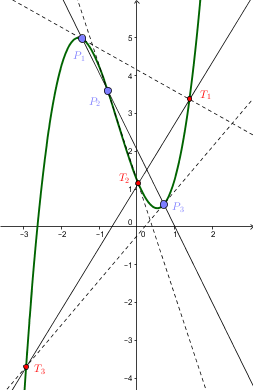
Cubic Function
In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d, that is, a polynomial function of degree three. In many texts, the ''coefficients'' , , , and are supposed to be real numbers, and the function is considered as a real function that maps real numbers to real numbers or as a complex function that maps complex numbers to complex numbers. In other cases, the coefficients may be complex numbers, and the function is a complex function that has the set of the complex numbers as its codomain, even when the domain is restricted to the real numbers. Setting produces a cubic equation of the form :ax^3+bx^2+cx+d=0, whose solutions are called roots of the function. The derivative of a cubic function is a quadratic function. A cubic function with real coefficients has either one or three real roots ( which may not be distinct); all odd-degree polynomials with real coefficients have at least one real root. The graph of a cubic function always has a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |