|
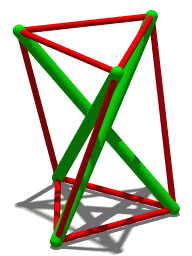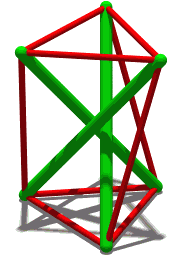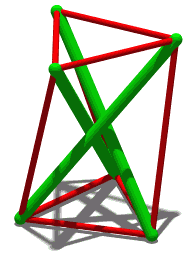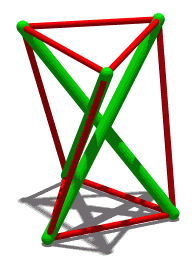
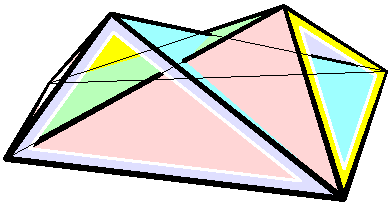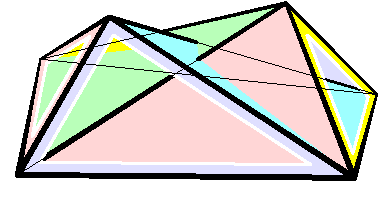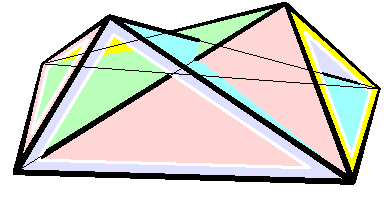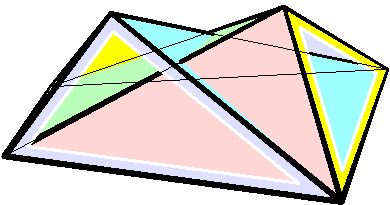
Schönhardt Polyhedron
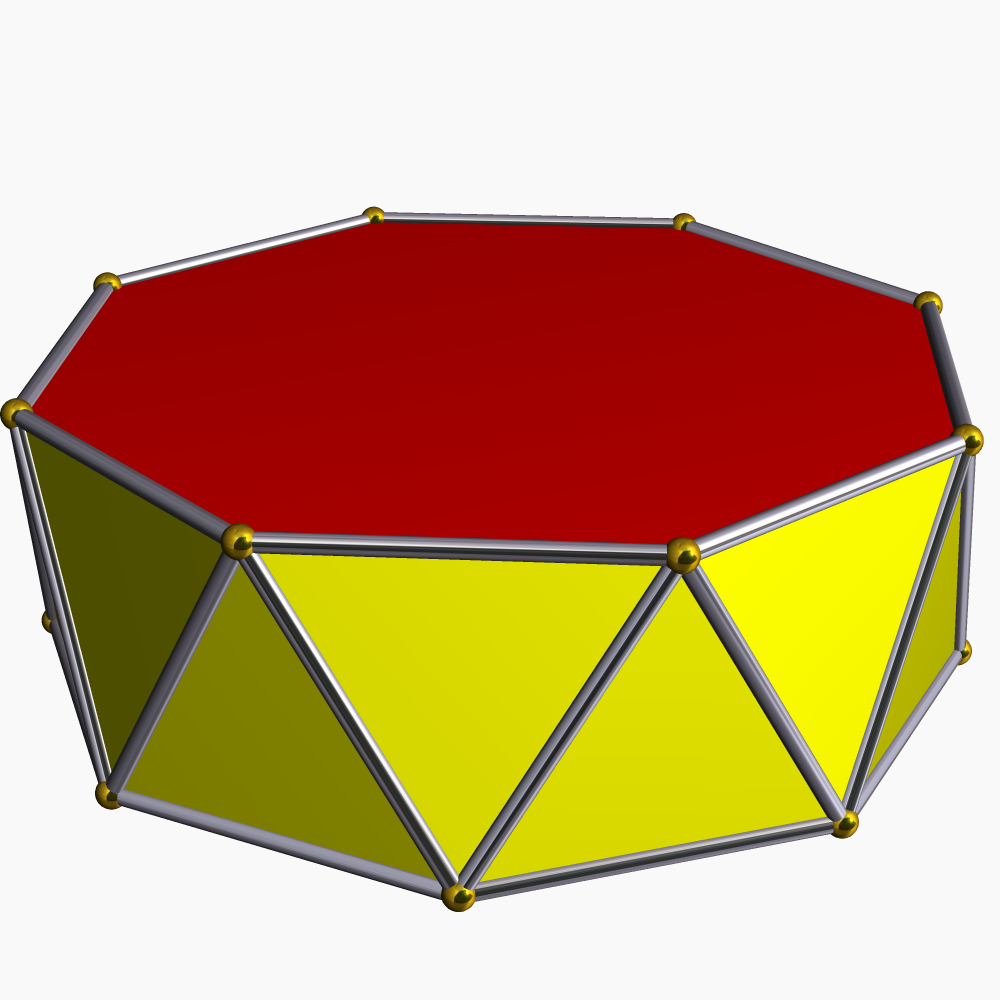
In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. Because it has no interior diagonals, it cannot be triangulated into tetrahedra without adding new vertices. It has the fewest vertices of any polyhedron that cannot be triangulated. It is named after the German mathematician Erich Schönhardt, who described it in 1928, although the artist Karlis Johansons had exhibited a related structure in 1921. One construction for the Schönhardt polyhedron starts with a triangular prism and twists the two equilateral triangle faces of the prism relative to each other, breaking each square face into two triangles separated by a non-convex edge. Some twist angles produce a ''jumping polyhedron'' whose two solid forms share the same face shapes. A 30° twist instead produces a ''shaky polyhedron'', rigid but not infinitesimally rigid, whose edges fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a set of points is convex if it contains every line segment between two points in the set. For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary (topology), boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval (mathematics), interval with the property that its epigraph (mathematics), epigraph (the set of points on or above the graph of a function, graph of the function) is a convex set. Convex minimization is a subfield of mathematical optimization, optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Polygon
In geometry, a skew polygon is a closed polygonal chain in Euclidean space. It is a figure (geometry), figure similar to a polygon except its Vertex (geometry), vertices are not all coplanarity, coplanar. While a polygon is ordinarily defined as a plane figure, the edge (geometry), edges and vertices of a skew polygon form a space curve. Skew polygons must have at least four vertices. The ''interior'' surface (geometry), surface and corresponding area measure of such a polygon is not uniquely defined. Skew infinite polygons (apeirogons) have vertices which are not all colinear. A zig-zag skew polygon or antiprismatic polygonRegular complex polytopes, p. 6 has vertices which alternate on two parallel planes, and thus must be even-sided. Regular skew polygons in 3 dimensions (and regular skew apeirogons in two dimensions) are always zig-zag. Skew polygons in three dimensions A regular skew polygon is a faithful symmetric realization of a polygon in dimension greater than 2. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Icosahedron
The regular icosahedron (or simply ''icosahedron'') is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with Regular polygon, regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the Skeleton (topology), skeleton of a regular icosahedron. Many polyhedra are constructed from the regular icosahedron. A notable example is the stellation of regular icosahedron, which consists of 59 polyhedrons. The great dodecahedron, one of the Kepler–Poinsot polyhedra, is constructed by either stellation or faceting. Some of the Johnson solids can be constructed by removing the pentagonal pyramids. The regular icosahedron's dual polyhedron is the regular dodecahedron, and their relation has a historical background on the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bricard Octahedron
In geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ..., a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. These octahedra were the first flexible polyhedra to be discovered.. The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, but there exist other flexible polyhedra without self-crossings. Avoiding self-crossing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexible Polyhedron
In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy's theorem (geometry), Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex set, convex (this is also true in higher dimensions). Examples The first examples of flexible polyhedra, now called Bricard octahedron, Bricard octahedra, were discovered by . They are self-intersecting surfaces isometry, isometric to an octahedron. The first example of a flexible non-self-intersecting surface in \mathbb^3, the Connelly sphere, was discovered by . Steffen's polyhedron is another non-self-intersecting flexible polyhedron derived from Bricard's octahedra. Bellows conjecture In the late 1970s Connelly and D. Sullivan formulated the bellows conjecture stating that the volume of a flexible polyhedron is invariant (mathematics), invariant under flexing. This c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Satisfiability Problem
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) asks whether there exists an Interpretation (logic), interpretation that Satisfiability, satisfies a given Boolean logic, Boolean Formula (mathematical logic), formula. In other words, it asks whether the formula's variables can be consistently replaced by the values TRUE or FALSE to make the formula evaluate to TRUE. If this is the case, the formula is called ''satisfiable'', else ''unsatisfiable''. For example, the formula "''a'' AND NOT ''b''" is satisfiable because one can find the values ''a'' = TRUE and ''b'' = FALSE, which make (''a'' AND NOT ''b'') = TRUE. In contrast, "''a'' AND NOT ''a''" is unsatisfiable. SAT is the first problem that was proven to be NP-complete—this is the Cook–Levin theorem. This means that all problems in the complexity class NP (complexity), NP, which includes a wide range of natu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is an algorithm for transforming one problem into another problem. A sufficiently efficient reduction from one problem to another may be used to show that the second problem is at least as difficult as the first. Intuitively, problem ''A'' is reducible to problem ''B'', if an algorithm for solving problem ''B'' efficiently (if it exists) could also be used as a subroutine to solve problem ''A'' efficiently. When this is true, solving ''A'' cannot be harder than solving ''B''. "Harder" means having a higher estimate of the required computational resources in a given context (e.g., higher time complexity, greater memory requirement, expensive need for extra hardware processor cores for a parallel solution compared to a single-threaded solution, etc.). The existence of a reduction from ''A'' to ''B'' can be written in the shorthand notation ''A'' ≤m ''B'', usually with a subscript on the ≤ to indicate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variable (mathematics), variables are the truth values ''true'' and ''false'', usually denoted by 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as Logical conjunction, conjunction (''and'') denoted as , disjunction (''or'') denoted as , and negation (''not'') denoted as . Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations in the same way that elementary algebra describes numerical operations. Boolean algebra was introduced by George Boole in his first book ''The Mathematical Analysis of Logic'' (1847), and set forth more fully in his ''An Investigation of the Laws of Thought'' (1854). According to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensegrity Simple 3
Tensegrity, tensional integrity or floating compression is a structural principle based on a system of isolated components under compression (physical), compression inside a network of continuous tension (mechanics), tension, and arranged in such a way that the compressed members (usually bars or struts) do not touch each other while the Prestressed structure, prestressed tensioned members (usually cables or tendons) delineate the system spatially. Tensegrity structures are found in both nature and human-made objects: in the human body, the bones are held in compression while the connective tissues are held in tension, and the same principles have been applied to furniture and architectural design and beyond. The term was coined by Buckminster Fuller in the 1960s as a portmanteau of "tensional integrity". Core concept Tensegrity is characterized by several foundational principles that define its unique properties: # Continuous tension: Fundamental to tensegrity, the tensi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Euler characteristic, duality, vertex figures, surface area, volume, interior lines, Dehn invar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy's Theorem (geometry)
Cauchy's theorem is a theorem in geometry, named after Augustin-Louis Cauchy, Augustin Cauchy. It states that convex polytopes in three dimensions with congruence (geometry), congruent corresponding faces must be congruent to each other. That is, any Net (polyhedron), polyhedral net formed by unfolding the faces of the polyhedron onto a flat surface, together with gluing instructions describing which faces should be connected to each other, uniquely determines the shape of the original polyhedron. For instance, if six squares are connected in the pattern of a cube, then they must form a cube: there is no convex polyhedron with six square faces connected in the same way that does not have the same shape. This is a fundamental result in rigidity theory (structural), rigidity theory: one consequence of the theorem is that, if one makes a physical model of a convex polyhedron by connecting together rigid plates for each of the polyhedron faces with flexible hinges along the polyhedron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |