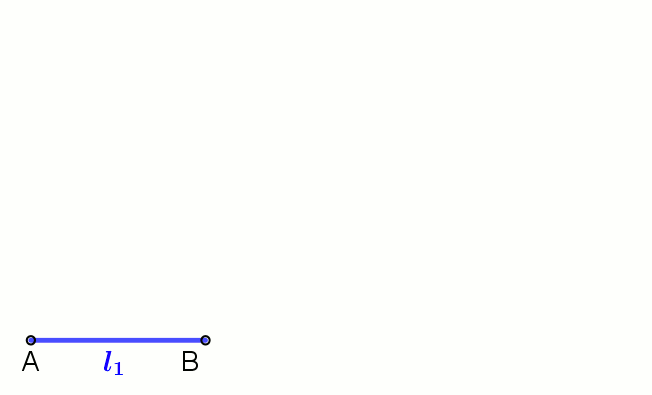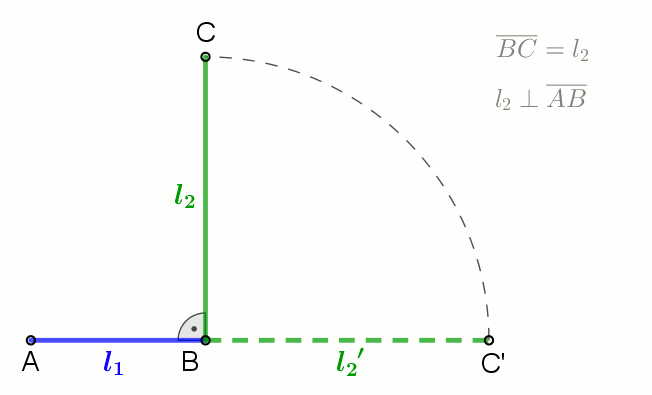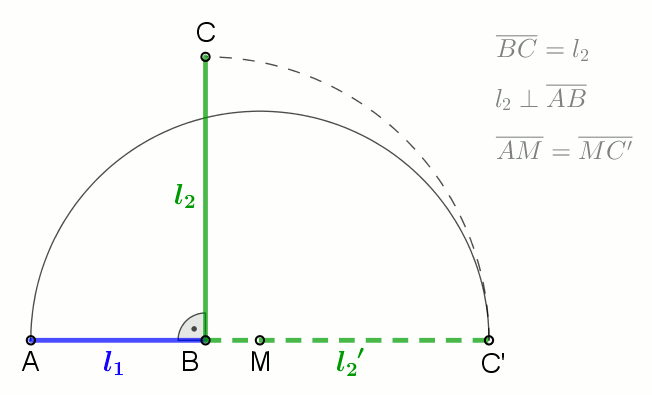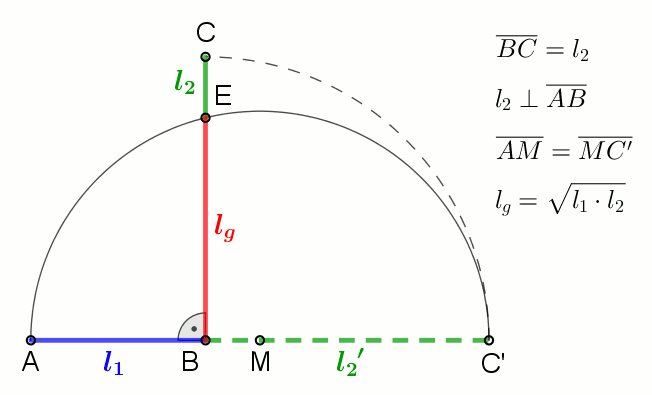|
Reduced Chi-squared Statistic
In statistics, the reduced chi-square statistic is used extensively in goodness of fit testing. It is also known as mean squared weighted deviation (MSWD) in isotopic dating and variance of unit weight in the context of weighted least squares. Its square root is called regression standard error, standard error of the regression, or standard error of the equation (see Ordinary least squares#Reduced chi-squared) Definition It is defined as chi-square per degree of freedom: :\chi^2_\nu = \frac \nu, where the chi-squared is a weighted sum of squared deviations: :\chi^2 = \sum_ with inputs: variance \sigma_i^2, observations ''O'', and calculated data ''C''. The degree of freedom, \nu = n - m, equals the number of observations ''n'' minus the number of fitted parameters ''m''. In weighted least squares, the definition is often written in matrix notation as :\chi^2_\nu = \frac, where ''r'' is the vector of residuals, and ''W'' is the weight matrix, the inverse of the input (diagon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geochronology
Geochronology is the science of determining the age of rocks, fossils, and sediments using signatures inherent in the rocks themselves. Absolute geochronology can be accomplished through radioactive isotopes, whereas relative geochronology is provided by tools such as paleomagnetism and stable isotope ratios. By combining multiple geochronological (and biostratigraphic) indicators the precision of the recovered age can be improved. Geochronology is different in application from biostratigraphy, which is the science of assigning sedimentary rocks to a known geological period via describing, cataloging and comparing fossil floral and faunal assemblages. Biostratigraphy does not ''directly'' provide an absolute age determination of a rock, but merely places it within an ''interval'' of time at which that fossil assemblage is known to have coexisted. Both disciplines work together hand in hand, however, to the point where they share the same system of naming strata (rock layers) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rasch Model
The Rasch model, named after Georg Rasch, is a psychometric model for analyzing categorical data, such as answers to questions on a reading assessment or questionnaire responses, as a function of the trade-off between the respondent's abilities, attitudes, or personality traits, and the item difficulty. For example, they may be used to estimate a student's reading ability or the extremity of a person's attitude to capital punishment from responses on a questionnaire. In addition to psychometrics and educational research, the Rasch model and its extensions are used in other areas, including the health profession, agriculture, and market research The mathematical theory underlying Rasch models is a special case of item response theory. However, there are important differences in the interpretation of the model parameters and its philosophical implications that separate proponents of the Rasch model from the item response modeling tradition. A central aspect of this divide relates t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations by the lower case Greek letter σ (sigma), for the population standard deviation, or the Latin letter '' s'', for the sample standard deviation. The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in practice less robust, than the average absolute deviation. A useful property of the standard deviation is that, unlike the variance, it is expressed in the same unit as the data. The standard deviation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thorium
Thorium is a weakly radioactive metallic chemical element with the symbol Th and atomic number 90. Thorium is silvery and tarnishes black when it is exposed to air, forming thorium dioxide; it is moderately soft and malleable and has a high melting point. Thorium is an electropositive actinide whose chemistry is dominated by the +4 oxidation state; it is quite reactive and can ignite in air when finely divided. All known thorium isotopes are unstable. The most stable isotope, 232Th, has a half-life of 14.05 billion years, or about the age of the universe; it decays very slowly via alpha decay, starting a decay chain named the thorium series that ends at stable 208 Pb. On Earth, thorium and uranium are the only significantly radioactive elements that still occur naturally in large quantities as primordial elements. Thorium is estimated to be over three times as abundant as uranium in the Earth's crust, and is chiefly refined from monazite sands as a by-product of e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helium
Helium (from el, ἥλιος, helios, lit=sun) is a chemical element with the symbol He and atomic number 2. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas and the first in the noble gas group in the periodic table. Its boiling and melting point are the lowest among all the elements. It is the second lightest and second most abundant element in the observable universe ( hydrogen is the lightest and most abundant). It is present at about 24% of the total elemental mass, which is more than 12 times the mass of all the heavier elements combined. Its abundance is similar to this in both the Sun and in Jupiter, due to the very high nuclear binding energy (per nucleon) of helium-4, with respect to the next three elements after helium. This helium-4 binding energy also accounts for why it is a product of both nuclear fusion and radioactive decay. The most common isotope of helium in the universe is helium-4, the vast majority of which was forme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uranium
Uranium is a chemical element with the symbol U and atomic number 92. It is a silvery-grey metal in the actinide series of the periodic table. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons. Uranium is weakly radioactive because all isotopes of uranium are unstable; the half-lives of its naturally occurring isotopes range between 159,200 years and 4.5 billion years. The most common isotopes in natural uranium are uranium-238 (which has 146 neutrons and accounts for over 99% of uranium on Earth) and uranium-235 (which has 143 neutrons). Uranium has the highest atomic weight of the primordially occurring elements. Its density is about 70% higher than that of lead, and slightly lower than that of gold or tungsten. It occurs naturally in low concentrations of a few parts per million in soil, rock and water, and is commercially extracted from uranium-bearing minerals such as uraninite. In nature, uranium is found as uranium-238 (99 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the '' mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is great ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Janet Hergt
Janet Margaret Hergt is an Australian geochemist. She is a Redmond Barry Distinguished Professor in the School of Earth Sciences at the University of Melbourne, Victoria, Australia. The main focus of her research has been in the chemical analysis of rocks and minerals to explore the exquisite record of Earth processes preserved within them. Hergt is best known for her geochemical investigations of magmatic rocks although she has employed similar techniques in interdisciplinary projects including areas of archaeological and biological science. Early life and education Hergt's earliest years were spent living on dairy farms in rural Victoria before moving to Frankston where she attended Karingal Primary School, and later Karingal High School. Hergt completed her undergraduate degree (BScHons) at La Trobe University in Melbourne in 1983, where she was awarded the David Myers University Medal and Ian Carlyle Medal in Geology. She received an Australian Government scholarship t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Arithmetic Mean
The weighted arithmetic mean is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics and also occurs in a more general form in several other areas of mathematics. If all the weights are equal, then the weighted mean is the same as the arithmetic mean. While weighted means generally behave in a similar fashion to arithmetic means, they do have a few counterintuitive properties, as captured for instance in Simpson's paradox. Examples Basic example Given two school with 20 students, one with 30 test grades in each class as follows: :Morning class = :Afternoon class = The mean for the morning class is 80 and the mean of the afternoon class is 90. The unweighted mean of the two means is 85. However, this does not account for the difference in number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |