|
Ramsey–Cass–Koopmans Model
The Ramsey–Cass–Koopmans model, or Ramsey growth model, is a neoclassical model of economic growth based primarily on the work of Frank P. Ramsey, with significant extensions by David Cass and Tjalling Koopmans. The Ramsey–Cass–Koopmans model differs from the Solow–Swan model in that the choice of consumption is explicitly microfounded at a point in time and so endogenizes the savings rate. As a result, unlike in the Solow–Swan model, the saving rate may not be constant along the transition to the long run steady state. Another implication of the model is that the outcome is Pareto optimal or Pareto efficient.This result is due not just to the endogeneity of the saving rate but also because of the infinite nature of the planning horizon of the agents in the model; it does not hold in other models with endogenous saving rates but more complex intergenerational dynamics, for example, in Samuelson's or Diamond's overlapping generations models. Originally Ramsey set out t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neoclassical Economics
Neoclassical economics is an approach to economics in which the production, consumption and valuation (pricing) of goods and services are observed as driven by the supply and demand model. According to this line of thought, the value of a good or service is determined through a hypothetical maximization of utility by income-constrained individuals and of profits by firms facing production costs and employing available information and factors of production. This approach has often been justified by appealing to rational choice theory, a theory that has come under considerable question in recent years. Neoclassical economics historically dominated macroeconomics and, together with Keynesian economics, formed the neoclassical synthesis which dominated mainstream economics as "neo-Keynesian economics" from the 1950s to the 1970s.Clark, B. (1998). ''Principles of political economy: A comparative approach''. Westport, Connecticut: Praeger. Nadeau, R. L. (2003). ''The Wealth of Na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representative Agent
Economists use the term representative agent to refer to the typical decision-maker of a certain type (for example, the typical consumer, or the typical firm). More technically, an economic model is said to have a representative agent if all agents of the same type are identical. Also, economists sometimes say a model has a representative agent when agents differ, but act in such a way that the sum of their choices is mathematically equivalent to the decision of one individual or many identical individuals. This occurs, for example, when preferences are Gorman aggregable. A model that contains many different agents whose choices cannot be aggregated in this way is called a heterogeneous agent model. The notion of the representative agent can be traced back to the late 19th century. Francis Edgeworth (1881) used the term "representative particular", while Alfred Marshall (1890) introduced a "representative firm" in his ''Principles of Economics''. However, after Robert Lucas, Jr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Discounting
In economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time (with or without uncertainty). Formally, exponential discounting occurs when total utility is given by :U(\_^)=\sum_^\delta^(u(c_t)), where ''c''''t'' is consumption at time ''t'', \delta is the exponential discount factor, and ''u'' is the instantaneous utility function. In continuous time, exponential discounting is given by :U(\_^)=\int_^ e^u(c(t))\,dt, Exponential discounting implies that the marginal rate of substitution between consumption at any pair of points in time depends only on how far apart those two points are. Exponential discounting is not dynamically inconsistent. A key aspect of the exponential discounting assumption is the property of dynamic consistency— preferences are constant over time. In other words, preferences do not change with the passage of time unless new information is presented. For example, consider an investment op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Rule
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let h(x)=f(x)/g(x), where both and are differentiable and g(x)\neq 0. The quotient rule states that the derivative of is :h'(x) = \frac. It is provable in many ways by using other derivative rules. Examples Example 1: Basic example Given h(x)=\frac, let f(x)=e^x, g(x)=x^2, then using the quotient rule:\begin \frac \left(\frac\right) &= \frac \\ &= \frac \\ &= \frac \\ &= \frac \\ &= \frac. \end Example 2: Derivatives of tangent and cotangent functions The quotient rule can be used to find the derivative of \tan x = \frac as follows:\begin \frac \tan x &= \frac \left(\frac\right) \\ &= \frac \\ &= \frac \\ &= \frac \\ &= \frac = \sec^2 x. \endSimilarly, the derivative of \cot x = \frac can be obtained as follows:\begin \frac \cot x &= \frac \left(\frac\right) \\ &= \frac \\ &= \fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Returns To Scale
In economics, returns to scale describe what happens to long-run returns as the scale of production increases, when all input levels including physical capital usage are variable (able to be set by the firm). The concept of returns to scale arises in the context of a firm's production function. It explains the long-run linkage of the rate of increase in output (production) relative to associated increases in the inputs (factors of production). In the long run, all factors of production are variable and subject to change in response to a given increase in production scale. While economies of scale show the effect of an increased output level on unit costs, returns to scale focus only on the relation between input and output quantities. There are three possible types of returns to scale: increasing returns to scale, constant returns to scale, and diminishing (or decreasing) returns to scale. If output increases by the same proportional change as all inputs change then there are cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Function
In mathematics, a homogeneous function is a function of several variables such that, if all its arguments are multiplied by a scalar, then its value is multiplied by some power of this scalar, called the degree of homogeneity, or simply the ''degree''; that is, if is an integer, a function of variables is homogeneous of degree if :f(sx_1,\ldots, sx_n)=s^k f(x_1,\ldots, x_n) for every x_1, \ldots, x_n, and s\ne 0. For example, a homogeneous polynomial of degree defines a homogeneous function of degree . The above definition extends to functions whose domain and codomain are vector spaces over a field : a function f : V \to W between two -vector spaces is ''homogeneous'' of degree k if for all nonzero s \in F and v \in V. This definition is often further generalized to functions whose domain is not , but a cone in , that is, a subset of such that \mathbf\in C implies s\mathbf\in C for every nonzero scalar . In the case of functions of several real variables and real vecto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inada Conditions
In macroeconomics, the Inada conditions, named after Japanese economist Ken-Ichi Inada, are assumptions about the shape of a function, usually applied to a production function or a utility function. When the production function of a neoclassical growth model satisfies the Inada conditions, then it guarantees the stability of an economic growth path. The conditions as such had been introduced by Hirofumi Uzawa. Statement Given a continuously differentiable function f \colon X \to Y, where X = \left\ and Y = \left\, the conditions are: #the value of the function f(\mathbf) at \mathbf = \mathbf is 0: f(\mathbf)=0 #the function is concave on X, i.e. the Hessian matrix \mathbf_ = \left( \frac \right) needs to be negative-semidefinite. Economically this implies that the marginal returns for input x_ are positive, i.e. \partial f(\mathbf)/\partial x_>0, but decreasing, i.e. \partial^ f(\mathbf)/ \partial x_^<0 #the |
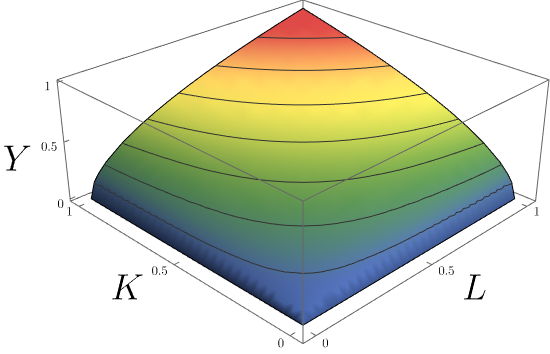
Cobb–Douglas Production Function
In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs (particularly physical capital and labor) and the amount of output that can be produced by those inputs. The Cobb–Douglas form was developed and tested against statistical evidence by Charles Cobb and Paul Douglas between 1927 and 1947; according to Douglas, the functional form itself was developed earlier by Philip Wicksteed. Formulation In its most standard form for production of a single good with two factors, the function is : Y=AL^\beta K^\alpha where: * ''Y'' = total production (the real value of all goods produced in a year or 365.25 days) * ''L'' = labour input (person-hours worked in a year or 365.25 days) * ''K'' = capital input (a measure of all machinery, equipment, and buildings; the value of capital input divided by the price of capi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aggregate Production Function
In economics, a production function gives the technological relation between quantities of physical inputs and quantities of output of goods. The production function is one of the key concepts of mainstream neoclassical theories, used to define marginal product and to distinguish allocative efficiency, a key focus of economics. One important purpose of the production function is to address allocative efficiency in the use of factor inputs in production and the resulting distribution of income to those factors, while abstracting away from the technological problems of achieving technical efficiency, as an engineer or professional manager might understand it. For modelling the case of many outputs and many inputs, researchers often use the so-called Shephard's distance functions or, alternatively, directional distance functions, which are generalizations of the simple production function in economics. In macroeconomics, aggregate production functions are estimated to create a fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Investment
Investment is the dedication of money to purchase of an asset to attain an increase in value over a period of time. Investment requires a sacrifice of some present asset, such as time, money, or effort. In finance, the purpose of investing is to generate a return from the invested asset. The return may consist of a gain (profit) or a loss realized from the sale of a property or an investment, unrealized capital appreciation (or depreciation), or investment income such as dividends, interest, or rental income, or a combination of capital gain and income. The return may also include currency gains or losses due to changes in the foreign currency exchange rates. Investors generally expect higher returns from riskier investments. When a low-risk investment is made, the return is also generally low. Similarly, high risk comes with a chance of high losses. Investors, particularly novices, are often advised to diversify their portfolio. Diversification has the statistical effec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Notation
In differential calculus, there is no single uniform notation for differentiation. Instead, various notations for the derivative of a function or variable have been proposed by various mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation (and its opposite operation, the antidifferentiation or indefinite integration) are listed below. Leibniz's notation The original notation employed by Gottfried Leibniz is used throughout mathematics. It is particularly common when the equation is regarded as a functional relationship between dependent and independent variables and . Leibniz's notation makes this relationship explicit by writing the derivative as :\frac. Furthermore, the derivative of at is therefore written :\frac(x)\text\frac\text\frac f(x). Higher derivatives are written as :\frac, \frac, \frac, \ldots, \frac. This i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capital Intensity
Capital intensity is the amount of fixed or real capital present in relation to other factors of production, especially labor. At the level of either a production process or the aggregate economy, it may be estimated by the capital to labor ratio, such as from the points along a capital/labor isoquant. Growth The use of tools and machinery makes labor more effective, so rising capital intensity (or "capital deepening") pushes up the productivity of labor. Capital intensive societies tend to have a higher standard of living over the long run. Calculations made by Robert Solow claimed that economic growth was mainly driven by technological progress (productivity growth) rather than inputs of capital and labor. However recent economic research has invalidated that theory, since Solow did not properly consider changes in both investment and labor inputs. Dale Jorgenson, of Harvard University, President of the American Economic Association in 2000, concludes that: 'Griliches and I show ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |