|
Ramsey Theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that focuses on the appearance of order in a substructure given a structure of a known size. Problems in Ramsey theory typically ask a question of the form: "how big must some structure be to guarantee that a particular property holds?" More specifically, Ron Graham described Ramsey theory as a "branch of combinatorics". Examples A typical result in Ramsey theory starts with some mathematical structure that is then cut into pieces. How big must the original structure be in order to ensure that at least one of the pieces has a given interesting property? This idea can be defined as partition regularity. For example, consider a complete graph of order ''n''; that is, there are ''n'' vertices and each vertex is connected to every other vertex by an edge. A complete graph of order 3 is called a triangle. Now colour each edge either red or blue. How large must ''n'' be i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frank P
Frank or Franks may refer to: People * Frank (given name) * Frank (surname) * Franks (surname) * Franks, a medieval Germanic people * Frank, a term in the Muslim world for all western Europeans, particularly during the Crusades - see Farang Currency * Liechtenstein franc or frank, the currency of Liechtenstein since 1920 * Swiss franc or frank, the currency of Switzerland since 1850 * Westphalian frank, currency of the Kingdom of Westphalia between 1808 and 1813 * The currencies of the German-speaking cantons of Switzerland (1803–1814): ** Appenzell frank ** Argovia frank ** Basel frank ** Berne frank ** Fribourg frank ** Glarus frank ** Graubünden frank ** Luzern frank ** Schaffhausen frank ** Schwyz frank ** Solothurn frank ** St. Gallen frank ** Thurgau frank ** Unterwalden frank ** Uri frank ** Zürich frank Places * Frank, Alberta, Canada, an urban community, formerly a village * Franks, Illinois, United States, an unincorporated community * Franks, Missouri, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Milliken–Taylor Theorem
In mathematics, the Milliken–Taylor theorem in combinatorics is a generalization of both Ramsey's theorem and Hindman's theorem. It is named after Keith Milliken and Alan D. Taylor. Let \mathcal_f(\mathbb) denote the set of finite subsets of \mathbb, and define a partial order on \mathcal_f(\mathbb) by α<β max α |
Ergodic Ramsey Theory
Ergodic Ramsey theory is a branch of mathematics where problems motivated by additive combinatorics are proven using ergodic theory. History Ergodic Ramsey theory arose shortly after Endre Szemerédi's proof that a set of positive upper density contains arbitrarily long arithmetic progressions, when Hillel Furstenberg gave a new proof of this theorem using ergodic theory. It has since produced combinatorial results, some of which have yet to be obtained by other means, and has also given a deeper understanding of the structure of measure-preserving dynamical systems. Szemerédi's theorem Szemerédi's theorem is a result in arithmetic combinatorics, concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured. that every set of integers ''A'' with positive natural density contains a ''k'' term arithmetic progression for every ''k''. This conjecture, which became Szemerédi's theorem, generalizes the statement of van der Waerden's theorem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal D'Analyse Mathématique
The ''Journal d'Analyse Mathématique'' is a triannual peer-reviewed scientific journal published by Magnes Press (Hebrew University of Jerusalem). It was established in 1951 by Binyamin Amirà. It covers research in mathematics, especially classical analysis and related areas such as complex function theory, ergodic theory, functional analysis, harmonic analysis, partial differential equations, and quasiconformal mapping. Abstracting and indexing The journal is abstracted and indexed in: *MathSciNet *Science Citation Index Expanded *Scopus *ZbMATH Open According to the ''Journal Citation Reports'', the journal has a 2021 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 1.132. References External links *{{Official website, 1=https://www.springer.com/mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Szemerédi's Theorem
In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured that every set of integers ''A'' with positive natural density contains a ''k''-term arithmetic progression for every ''k''. Endre Szemerédi proved the conjecture in 1975. Statement A subset ''A'' of the natural numbers is said to have positive upper density if :\limsup_\frac > 0. Szemerédi's theorem asserts that a subset of the natural numbers with positive upper density contains infinitely many arithmetic progressions of length ''k'' for all positive integers ''k''. An often-used equivalent finitary version of the theorem states that for every positive integer ''k'' and real number \delta \in (0, 1], there exists a positive integer :N = N(k,\delta) such that every subset of of size at least δ''N'' contains an arithmetic progression of length ''k''. Another formulation uses the function ''r''''k''(''N''), th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turán's Theorem
In graph theory, Turán's theorem bounds the number of edges that can be included in an undirected graph that does not have a complete subgraph of a given size. It is one of the central results of extremal graph theory, an area studying the largest or smallest graphs with given properties, and is a special case of the forbidden subgraph problem on the maximum number of edges in a graph that does not have a given subgraph. An example of an n- vertex graph that does not contain any (r+1)-vertex clique K_ may be formed by partitioning the set of n vertices into r parts of equal or nearly equal size, and connecting two vertices by an edge whenever they belong to two different parts. The resulting graph is the Turán graph T(n,r). Turán's theorem states that the Turán graph has the largest number of edges among all -free -vertex graphs. Turán's theorem, and the Turán graphs giving its extreme case, were first described and studied by Hungarian mathematician Pál Turán in 1941. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
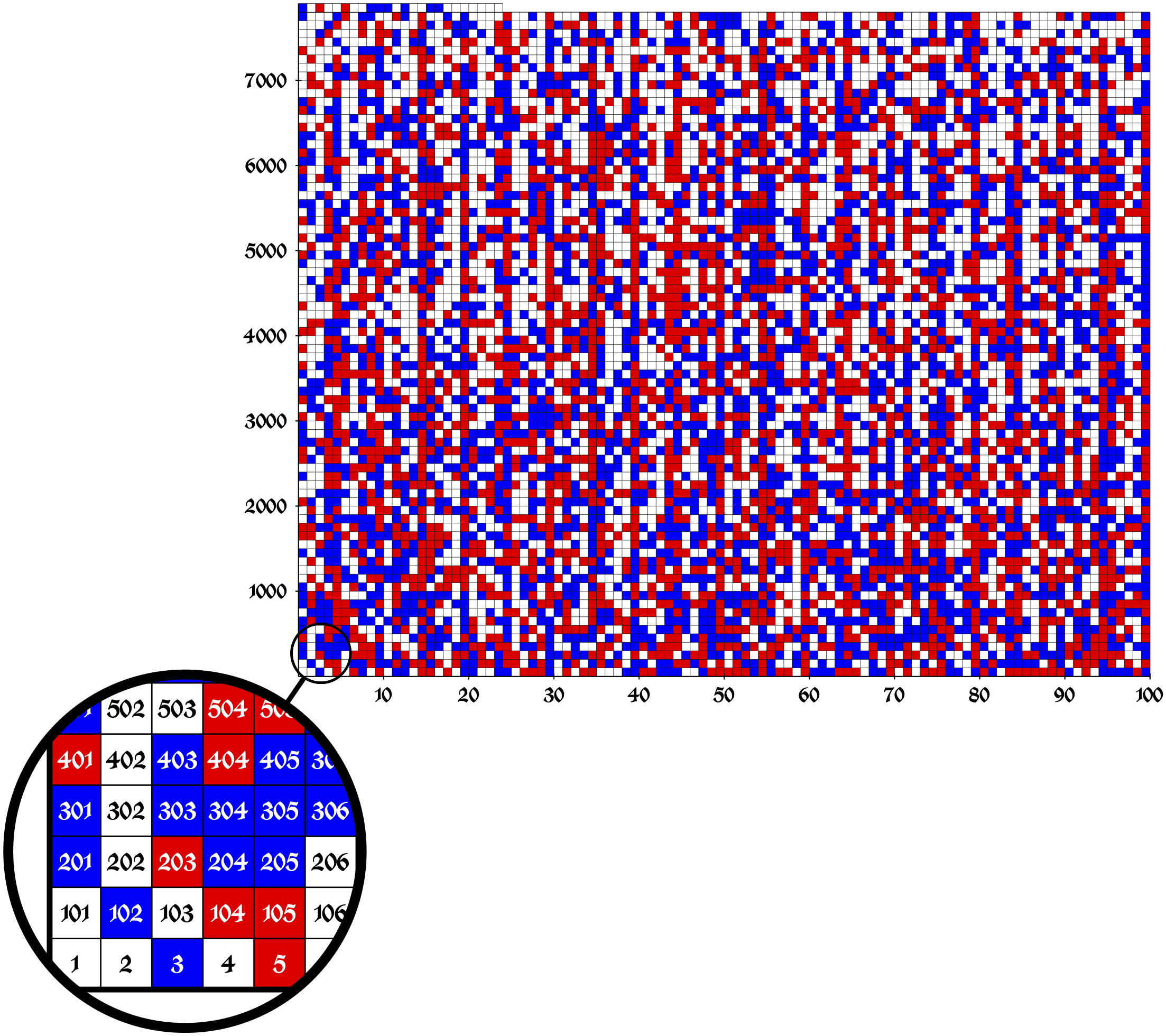
Boolean Pythagorean Triples Problem
The Boolean Pythagorean triples problem is a problem from Ramsey theory about whether the positive integers can be colored red and blue so that no Pythagorean triples consist of all red or all blue members. The Boolean Pythagorean triples problem was solved by Marijn Heule, Oliver Kullmann and Victor W. Marek in May 2016 through a computer-assisted proof. Statement The problem asks if it is possible to color each of the positive integers either red or blue, so that no Pythagorean triple of integers ''a'', ''b'', ''c'', satisfying a^2+b^2=c^2 are all the same color. For example, in the Pythagorean triple 3, 4 and 5 (3^2+4^2=5^2), if 3 and 4 are colored red, then 5 must be colored blue. Solution Marijn Heule, Oliver Kullmann and Victor W. Marek showed that such a coloring is only possible up to the number 7824. The actual statement of the theorem proved is There are possible coloring combinations for the numbers up to 7825. These possible colorings were logically and algorithm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graham's Number
Graham's number is an immense number that arose as an upper bound on the answer of a problem in the mathematical field of Ramsey theory. It is much larger than many other large numbers such as Skewes's number and Moser's number, both of which are in turn much larger than a googolplex. As with these, it is so large that the observable universe is far too small to contain an ordinary digital representation of Graham's number, assuming that each digit occupies one Planck volume, possibly the smallest measurable space. But even the number of digits in this digital representation of Graham's number would itself be a number so large that its digital representation cannot be represented in the observable universe. Nor even can the number of digits of ''that'' number—and so forth, for a number of times far exceeding the total number of Planck volumes in the observable universe. Thus Graham's number cannot be expressed even by physical universe-scale power towers of the form a ^. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paris–Harrington Theorem
In mathematical logic, the Paris–Harrington theorem states that a certain combinatorial principle in Ramsey theory, namely the strengthened finite Ramsey theorem, is true, but not provable in Peano arithmetic. This has been described by some (such as the editor of the ''Handbook of Mathematical Logic'' in the references below) as the first "natural" example of a true statement about the integers that could be stated in the language of arithmetic, but not proved in Peano arithmetic; it was already known that such statements existed by Gödel's first incompleteness theorem. Strengthened finite Ramsey theorem The strengthened finite Ramsey theorem is a statement about colorings and natural numbers and states that: : For any positive integers ''n'', ''k'', ''m'', such that ''m ≥ n'', one can find ''N'' with the following property: if we color each of the ''n''-element subsets of ''S'' = with one of ''k'' colors, then we can find a subset ''Y'' of ''S'' with at least ''m'' elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Recursive
In computability theory, a primitive recursive function is roughly speaking a function that can be computed by a computer program whose loops are all "for" loops (that is, an upper bound of the number of iterations of every loop can be determined before entering the loop). Primitive recursive functions form a strict subset of those general recursive functions that are also total functions. The importance of primitive recursive functions lies in the fact that most computable functions that are studied in number theory (and more generally in mathematics) are primitive recursive. For example, addition and division, the factorial and exponential function, and the function which returns the ''n''th prime are all primitive recursive. In fact, for showing that a computable function is primitive recursive, it suffices to show that its time complexity is bounded above by a primitive recursive function of the input size. It is hence not that easy to devise a computable function that is ''n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ackermann Function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive. All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive. After Ackermann's publication of his function (which had three non-negative integer arguments), many authors modified it to suit various purposes, so that today "the Ackermann function" may refer to any of numerous variants of the original function. One common version, the two-argument Ackermann–Péter function is defined as follows for nonnegative integers ''m'' and ''n'': : \begin \operatorname(0, n) & = & n + 1 \\ \operatorname(m+1, 0) & = & \operatorname(m, 1) \\ \operatorname(m+1, n+1) & = & \operatorname(m, \operatorname(m+1, n)) \end Its value grows rapidly, even for small inputs. For example, is an integer o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Growth
Exponential growth is a process that increases quantity over time. It occurs when the instantaneous rate of change (that is, the derivative) of a quantity with respect to time is proportional to the quantity itself. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent (in contrast to other types of growth, such as quadratic growth). If the constant of proportionality is negative, then the quantity decreases over time, and is said to be undergoing exponential decay instead. In the case of a discrete domain of definition with equal intervals, it is also called geometric growth or geometric decay since the function values form a geometric progression. The formula for exponential growth of a variable at the growth rate , as time goes on in discrete intervals (that is, at integer times 0, 1, 2, 3, ...), is x_t = x_0(1+r)^t where is the value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |