|
Ring Wave Guide
In quantum mechanics, the case of a particle in a one-dimensional ring is similar to the particle in a box. The Schrödinger equation for a free particle which is restricted to a ring (technically, whose configuration space is the circle S^1) is : -\frac\nabla^2 \psi = E\psi Wave function Using polar coordinates on the 1-dimensional ring of radius R, the wave function depends only on the angular coordinate, and so : \nabla^2 = \frac \frac Requiring that the wave function be periodic in \ \theta with a period 2 \pi (from the demand that the wave functions be single-valued functions on the circle), and that they be normalized leads to the conditions : \int_^ \left, \psi ( \theta ) \^2 \, d\theta = 1\ , and : \ \psi (\theta) = \ \psi ( \theta + 2\pi) Under these conditions, the solution to the Schrödinger equation is given by : \psi_(\theta) = \frac\, e^ Energy eigenvalues The energy eigenvalues E are quantized because of the periodic boundary conditions, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Condition
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems, in the linear case, involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential equations is devote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
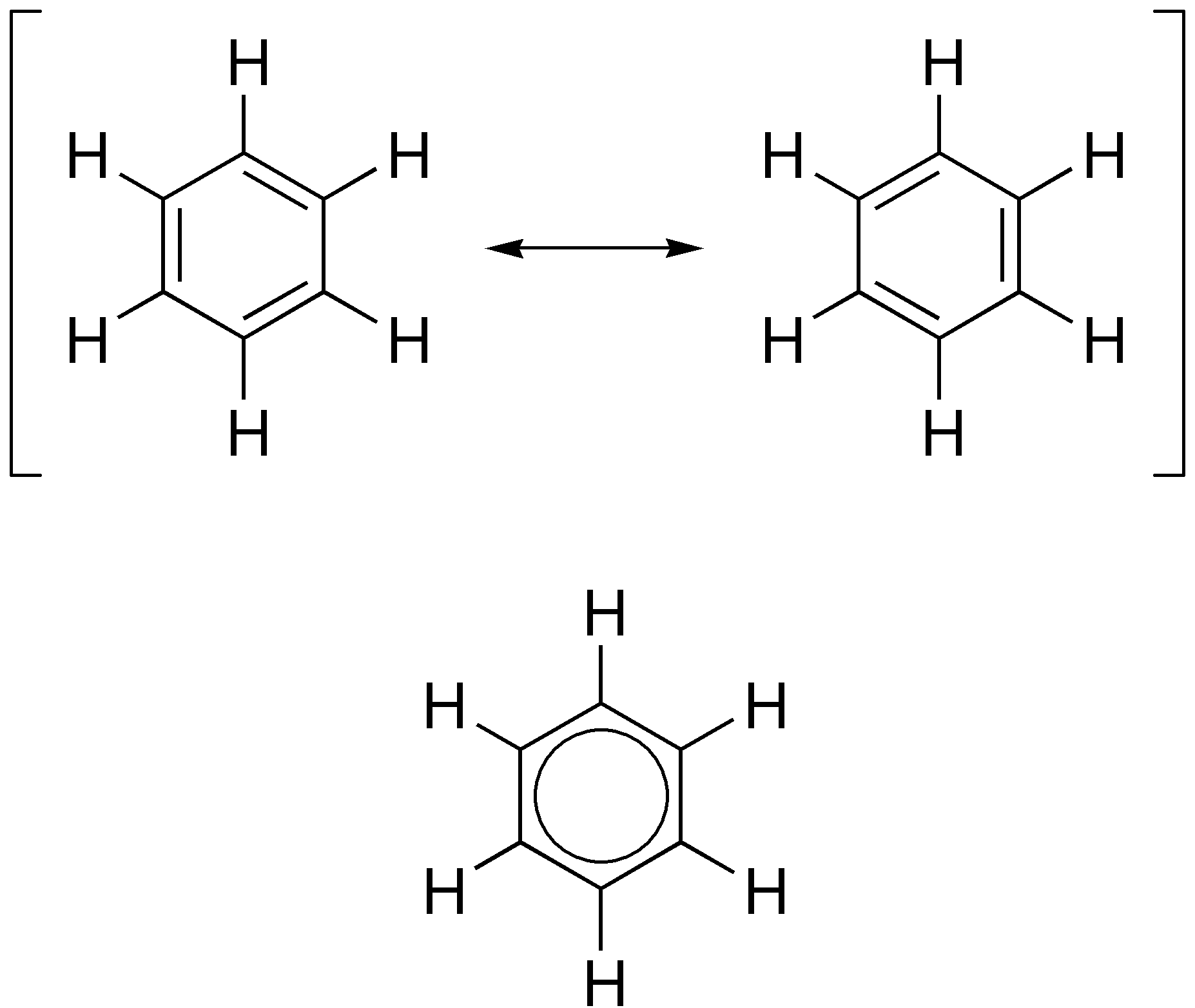
Friedrich August Kekulé Von Stradonitz
Friedrich may refer to: Names *Friedrich (given name), people with the given name ''Friedrich'' *Friedrich (surname), people with the surname ''Friedrich'' Other *Friedrich (board game), a board game about Frederick the Great and the Seven Years' War * ''Friedrich'' (novel), a novel about anti-semitism written by Hans Peter Richter *Friedrich Air Conditioning, a company manufacturing air conditioning and purifying products *, a German cargo ship in service 1941-45 See also *Friedrichs (other) *Frederick (other) *Nikolaus Friedreich Nikolaus Friedreich (1 July 1825 in Würzburg – 6 July 1882 in Heidelberg) was a German pathologist and neurologist, and a third generation physician in the Friedreich family. His father was psychiatrist Johann Baptist Friedreich (1796–18 ... {{disambig ja:フリードリヒ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benzene
Benzene is an Organic compound, organic chemical compound with the Chemical formula#Molecular formula, molecular formula C6H6. The benzene molecule is composed of six carbon atoms joined in a planar hexagonal Ring (chemistry), ring with one hydrogen atom attached to each. Because it contains only carbon and hydrogen atoms, benzene is classed as a hydrocarbon. Benzene is a natural constituent of petroleum and is one of the elementary petrochemicals. Due to the cyclic continuous pi bonds between the carbon atoms, benzene is classed as an aromatic hydrocarbon. Benzene is a colorless and highly Combustibility and flammability, flammable liquid with a sweet smell, and is partially responsible for the aroma of gasoline. It is used primarily as a Precursor (chemistry), precursor to the manufacture of chemicals with more complex structures, such as ethylbenzene and cumene, of which billions of kilograms are produced annually. Although benzene is a major Chemical industry, industrial che ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aromatic
In organic chemistry, aromaticity is a chemical property describing the way in which a conjugated system, conjugated ring of unsaturated bonds, lone pairs, or empty orbitals exhibits a stabilization stronger than would be expected from conjugation alone. The earliest use of the term was in an article by August Wilhelm Hofmann in 1855. There is no general relationship between aromaticity as a chemical property and the olfaction, olfactory properties of such compounds. Aromaticity can also be considered a manifestation of cyclic delocalization and of Resonance (chemistry), resonance. This is usually considered to be because electrons are free to cycle around circular arrangements of atoms that are alternately single- and double-covalent bond, bonded to one another. This commonly seen model of aromatic rings, namely the idea that benzene was formed from a six-membered carbon ring with alternating single and double bonds (cyclohexatriene), was developed by Friedrich August Kekulé ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Organic Chemistry
Organic chemistry is a subdiscipline within chemistry involving the science, scientific study of the structure, properties, and reactions of organic compounds and organic matter, organic materials, i.e., matter in its various forms that contain carbon atoms.Clayden, J.; Greeves, N. and Warren, S. (2012) ''Organic Chemistry''. Oxford University Press. pp. 1–15. . Study of structure determines their structural formula. Study of properties includes Physical property, physical and Chemical property, chemical properties, and evaluation of Reactivity (chemistry), chemical reactivity to understand their behavior. The study of organic reactions includes the organic synthesis, chemical synthesis of natural products, drugs, and polymers, and study of individual organic molecules in the laboratory and via theoretical (in silico) study. The range of chemicals studied chemistry includes hydrocarbons (compounds containing only carbon and hydrogen) as well as compounds based on carbon, but a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Series
A Fourier series () is an Series expansion, expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always Convergent series, converge. Well-behaved functions, for example Smoothness, smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Theorem
A Fourier series () is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in . The study of the conv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Superposition
Quantum superposition is a fundamental principle of quantum mechanics that states that linear combinations of solutions to the Schrödinger equation are also solutions of the Schrödinger equation. This follows from the fact that the Schrödinger equation is a linear differential equation in time and position. More precisely, the state of a system is given by a linear combination of all the eigenfunctions of the Schrödinger equation governing that system. An example is a qubit used in quantum information processing. A qubit state is most generally a superposition of the basis states , 0 \rangle and , 1 \rangle: : , \Psi \rangle = c_0, 0\rangle + c_1, 1\rangle, where , \Psi \rangle is the quantum state of the qubit, and , 0 \rangle, , 1 \rangle denote particular solutions to the Schrödinger equation in Dirac notation weighted by the two probability amplitudes c_0 and c_1 that both are complex numbers. Here , 0 \rangle corresponds to the classical 0 bit, and , 1 \r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenfunction
In mathematics, an eigenfunction of a linear operator ''D'' defined on some function space is any non-zero function f in that space that, when acted upon by ''D'', is only multiplied by some scaling factor called an eigenvalue. As an equation, this condition can be written as Df = \lambda f for some scalar eigenvalue \lambda. The solutions to this equation may also be subject to boundary conditions that limit the allowable eigenvalues and eigenfunctions. An eigenfunction is a type of eigenvector. Eigenfunctions In general, an eigenvector of a linear operator ''D'' defined on some vector space is a nonzero vector in the domain of ''D'' that, when ''D'' acts upon it, is simply scaled by some scalar value called an eigenvalue. In the special case where ''D'' is defined on a function space, the eigenvectors are referred to as eigenfunctions. That is, a function ''f'' is an eigenfunction of ''D'' if it satisfies the equation where λ is a scalar. The solutions to Equation may also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuth
An azimuth (; from ) is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system. Mathematically, the relative position vector from an observer ( origin) to a point of interest is projected perpendicularly onto a reference plane (the horizontal plane); the angle between the projected vector and a reference vector on the reference plane is called the azimuth. When used as a celestial coordinate, the azimuth is the horizontal direction of a star or other astronomical object in the sky. The star is the point of interest, the reference plane is the local area (e.g. a circular area with a 5 km radius at sea level) around an observer on Earth's surface, and the reference vector points to true north. The azimuth is the angle between the north vector and the star's vector on the horizontal plane. Azimuth is usually measured in degrees (°), in the positive range 0° to 360° or in the signed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Nucleus
The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford at the Department_of_Physics_and_Astronomy,_University_of_Manchester , University of Manchester based on the 1909 Geiger–Marsden experiments, Geiger–Marsden gold foil experiment. After the discovery of the neutron in 1932, models for a nucleus composed of protons and neutrons were quickly developed by Dmitri Ivanenko and Werner Heisenberg. An atom is composed of a positively charged nucleus, with a cloud of negatively charged electrons surrounding it, bound together by electrostatic force. Almost all of the mass of an atom is located in the nucleus, with a very small contribution from the electron cloud. Protons and neutrons are bound together to form a nucleus by the nuclear force. The diameter of the nucleus is in the range of () for hydrogen (the diameter of a single proton) to about for uranium. These dimensions are much ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |