|
Quasi-isometry
In mathematics, a quasi-isometry is a function between two metric spaces that respects large-scale geometry of these spaces and ignores their small-scale details. Two metric spaces are quasi-isometric if there exists a quasi-isometry between them. The property of being quasi-isometric behaves like an equivalence relation on the class of metric spaces. The concept of quasi-isometry is especially important in geometric group theory, following the work of Gromov. Definition Suppose that f is a (not necessarily continuous) function from one metric space (M_1,d_1) to a second metric space (M_2,d_2). Then f is called a ''quasi-isometry'' from (M_1,d_1) to (M_2,d_2) if there exist constants A\ge 1, B\ge 0, and C\ge 0 such that the following two properties both hold:P. de la Harpe, ''Topics in geometric group theory''. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 2000. #For every two points x and y in M_1, the distance between their images is up to the a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups can act non-trivially (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology, hyperbolic geometry, algebraic topology, computational group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a Conceptual metaphor , metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
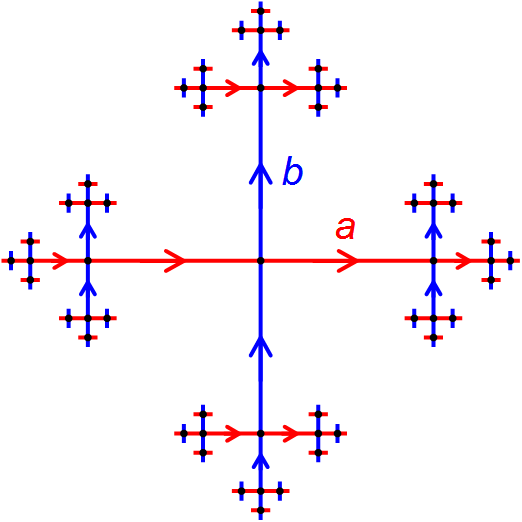
Švarc–Milnor Lemma
In the mathematical subject of geometric group theory, the Švarc–Milnor lemma (sometimes also called Milnor–Švarc lemma, with both variants also sometimes spelling Švarc as Schwarz) is a statement which says that a group G, equipped with a "nice" discrete isometric action on a metric space X, is quasi-isometric to X. This result goes back, in different form, before the notion of quasi-isometry was formally introduced, to the work of Albert S. Schwarz (1955) and John Milnor (1968). Pierre de la Harpe called the Švarc–Milnor lemma "the ''fundamental observation in geometric group theory''"Pierre de la Harpe, Topics in geometric group theory'. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 2000. ; p. 87 because of its importance for the subject. Occasionally the name "fundamental observation in geometric group theory" is now used for this statement, instead of calling it the Švarc–Milnor lemma; see, for example, Theorem 8.2 in the book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gromov's Theorem On Groups Of Polynomial Growth
In geometric group theory, Gromov's theorem on groups of polynomial growth, first proved by Mikhail Gromov, characterizes finitely generated groups of ''polynomial'' growth, as those groups which have nilpotent subgroups of finite index. Statement The growth rate of a group is a well-defined notion from asymptotic analysis. To say that a finitely generated group has polynomial growth means the number of elements of length at most ''n'' (relative to a symmetric generating set) is bounded above by a polynomial function ''p''(''n''). The ''order of growth'' is then the least degree of any such polynomial function ''p''. A nilpotent group ''G'' is a group with a lower central series terminating in the identity subgroup. Gromov's theorem states that a finitely generated group has polynomial growth if and only if it has a nilpotent subgroup that is of finite index. Growth rates of nilpotent groups There is a vast literature on growth rates, leading up to Gromov's theorem. An earli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant (mathematics)
In mathematics, an invariant is a property of a mathematical object (or a class of mathematical objects) which remains unchanged after operations or transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class. Invariants are used in diverse areas of mathematics such as geometry, topology, algebra and discrete mathematics. Some important classes of transformations are defined by an invariant they leave unchanged. For example, conformal maps are defined as transformations of the plane that preserve angles. The discovery of invariants is an import ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automatic Group
In mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata represent the Cayley graph of the group. That is, they can tell whether a given word representation of a group element is in a "canonical form" and can tell whether two elements given in canonical words differ by a generator. More precisely, let ''G'' be a group and ''A'' be a finite set of generators. Then an ''automatic structure'' of ''G'' with respect to ''A'' is a set of finite-state automata: * the ''word-acceptor'', which accepts for every element of ''G'' at least one word in A^\ast representing it; *''multipliers'', one for each a \in A \cup \, which accept a pair (''w''1, ''w''2), for words ''w''''i'' accepted by the word-acceptor, precisely when w_1 a = w_2 in ''G''. The property of being automatic does not depend on the set of generators. Properties Automatic groups have word problem solvable in quadratic time. More strongly, a given wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word Problem For Groups
A word is a basic element of language that carries meaning, can be used on its own, and is uninterruptible. Despite the fact that language speakers often have an intuitive grasp of what a word is, there is no consensus among linguists on its definition and numerous attempts to find specific criteria of the concept remain controversial. Different standards have been proposed, depending on the theoretical background and descriptive context; these do not converge on a single definition. Some specific definitions of the term "word" are employed to convey its different meanings at different levels of description, for example based on phonological, grammatical or orthographic basis. Others suggest that the concept is simply a convention used in everyday situations. The concept of "word" is distinguished from that of a morpheme, which is the smallest unit of language that has a meaning, even if it cannot stand on its own. Words are made out of at least one morpheme. Morphemes can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Google Maps
Google Maps is a web mapping platform and consumer application offered by Google. It offers satellite imagery, aerial photography, street maps, 360° interactive panorama, interactive panoramic views of streets (Google Street View, Street View), real-time traffic conditions, and route planner, route planning for traveling by foot, car, bike, air (in Software release life cycle#Beta, beta) and public transportation. , Google Maps was being used by over one billion people every month around the world. Google Maps began as a C++ desktop program developed by brothers Lars Rasmussen (software developer), Lars and Jens Eilstrup Rasmussen, Jens Rasmussen, Stephen Ma and Noel Gordon in Australia at Where 2 Technologies. In October 2004, the company was acquired by Google, which converted it into a web application. After additional acquisitions of a geospatial data visualization company and a real-time traffic analyzer, Google Maps was launched in February 2005. The service's Front and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mostow Rigidity Theorem
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a complete, finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique. The theorem was proven for closed manifolds by and extended to finite volume manifolds by in 3 dimensions, and by in all dimensions at least 3. gave an alternate proof using the Gromov norm. gave the simplest available proof. While the theorem shows that the deformation space of (complete) hyperbolic structures on a finite volume hyperbolic n-manifold (for n >2) is a point, for a hyperbolic surface of genus g>1 there is a moduli space of dimension 6g-6 that parameterizes all metrics of constant curvature (up to diffeomorphism), a fact essential for Teichmüller theory. There is also a rich theory of deformation spaces of hyperbolic structures on ''infinite'' volume manifolds in three dimensions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |