|
Piecewise Linear Continuation
Simplicial continuation, or piecewise linear continuation (Allgower and Georg),Eugene L. Allgower, K. Georg, "Introduction to Numerical Continuation Methods", ''SIAM Classics in Applied Mathematics'' 45, 2003.E. L. Allgower, K. Georg, "Simplicial and Continuation Methods for Approximating Fixed Points and Solutions to Systems of Equations", ''SIAM Review'', Volume 22, 28-85, 1980. is a one-parameter continuation method which is well suited to small to medium embedding spaces. The algorithm has been generalized to compute higher-dimensional manifolds by (Allgower and Gnutzman)Eugene L. Allgower, Stefan Gnutzmann, "An Algorithm for Piecewise Linear Approximation of Implicitly Defined Two-Dimensional Surfaces", ''SIAM Journal on Numerical Analysis'', Volume 24, Number 2, 452-469, 1987. and (Allgower and Schmidt).Eugene L. Allgower, Phillip H. Schmidt, "An Algorithm for Piecewise-Linear Approximation of an Implicitly Defined Manifold", ''SIAM Journal on Numerical Analysis'', Volume 22, N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Continuation
Numerical continuation is a method of computing approximate solutions of a system of parameterized nonlinear equations, :F(\mathbf u,\lambda) = 0. The ''parameter'' \lambda is usually a real scalar, and the ''solution'' \mathbf u an ''n''-vector. For a fixed ''parameter value'' \lambda, F(\ast,\lambda) maps Euclidean n-space into itself. Often the original mapping F is from a Banach space into itself, and the Euclidean n-space is a finite-dimensional Banach space. A steady state, or fixed point, of a parameterized family of flows or maps are of this form, and by discretizing trajectories of a flow or iterating a map, periodic orbits and heteroclinic orbits can also be posed as a solution of F=0. Other forms In some nonlinear systems, parameters are explicit. In others they are implicit, and the system of nonlinear equations is written :F(\mathbf u) = 0 where \mathbf u is an ''n''-vector, and its image F(\mathbf u) is an ''n-1'' vector. This formulation, without an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty). For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary of a convex set is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling or experimentation, which represent the values of a function for a limited number of values of the independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gain in simplicity may outweigh the loss from interpolation error and give better performance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barycentric Coordinates (mathematics)
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane, a tetrahedron for points in three-dimensional space, etc.). The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass (or ''barycenter'') of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex. Every point has barycentric coordinates, and their sum is not zero. Two tuples of barycentric coordinates specify the same point if and only if they are proportional; that is to say, if one tuple can be obtained by multiplying the elements of the other tuple by the same non-zero number. Therefore, barycentric coordinates are either considered to be defined up to multiplication by a nonzero constant, or normalized for summing to unity. Barycentric coordina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Independence
In the theory of vector spaces, a set of vectors is said to be if there is a nontrivial linear combination of the vectors that equals the zero vector. If no such linear combination exists, then the vectors are said to be . These concepts are central to the definition of dimension. A vector space can be of finite dimension or infinite dimension depending on the maximum number of linearly independent vectors. The definition of linear dependence and the ability to determine whether a subset of vectors in a vector space is linearly dependent are central to determining the dimension of a vector space. Definition A sequence of vectors \mathbf_1, \mathbf_2, \dots, \mathbf_k from a vector space is said to be ''linearly dependent'', if there exist scalars a_1, a_2, \dots, a_k, not all zero, such that :a_1\mathbf_1 + a_2\mathbf_2 + \cdots + a_k\mathbf_k = \mathbf, where \mathbf denotes the zero vector. This implies that at least one of the scalars is nonzero, say a_1\ne 0, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
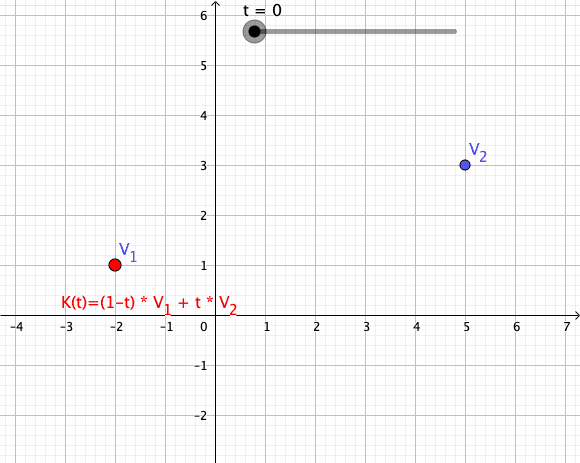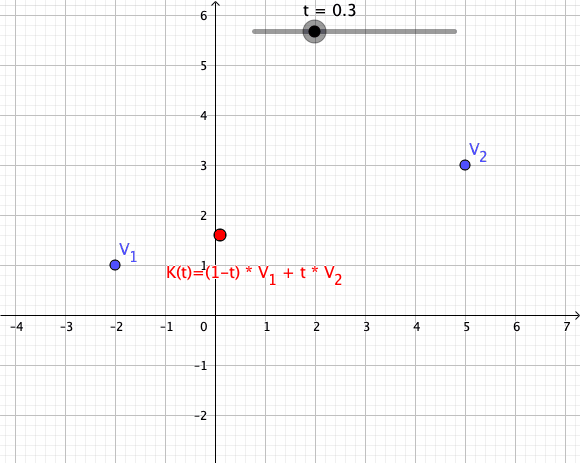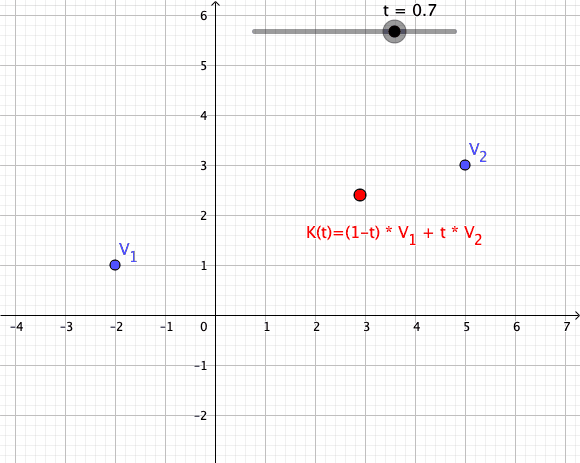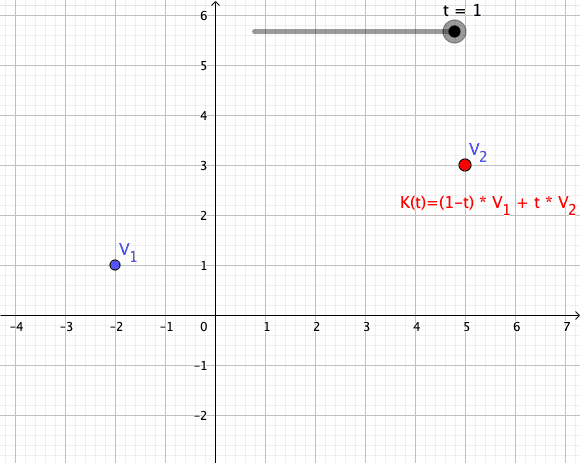
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is ident ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example, * a 0-dimensional simplex is a point, * a 1-dimensional simplex is a line segment, * a 2-dimensional simplex is a triangle, * a 3-dimensional simplex is a tetrahedron, and * a 4-dimensional simplex is a 5-cell. Specifically, a ''k''-simplex is a ''k''-dimensional polytope which is the convex hull of its ''k'' + 1 vertices. More formally, suppose the ''k'' + 1 points u_0, \dots, u_k \in \mathbb^ are affinely independent, which means u_1 - u_0,\dots, u_k-u_0 are linearly independent. Then, the simplex determined by them is the set of points : C = \left\ This representation in terms of weighted vertices is known as the barycentric coordinate system. A regular simplex is a simplex that is also a regular poly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contours , a type of Brit ...
Contour may refer to: * Contour (linguistics), a phonetic sound * Pitch contour * Contour (camera system), a 3D digital camera system * Contour, the KDE Plasma 4 interface for tablet devices * Contour line, a curve along which the function has a constant value * Contour drawing, an artistic technique * A closed path in the mathematical method of contour integration * Boundary (topology) of a set Contours may refer to: * ''Contours'' (album), by Sam Rivers * The Contours, a soul music group Contouring may refer to: * The makeup technique contouring Other uses * Ford Contour, a motor car * CONTOUR, a failed NASA space probe * Contour, a North Wing Apache ultralight aircraft variant See also * Contour fort Hillforts in Britain refers to the various hillforts within the island of Great Britain. Although the earliest such constructs fitting this description come from the Neolithic British Isles, with a few also dating to later Bronze Age Britain, Britis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Thurston
William Paul Thurston (October 30, 1946August 21, 2012) was an American mathematician. He was a pioneer in the field of low-dimensional topology and was awarded the Fields Medal in 1982 for his contributions to the study of 3-manifolds. Thurston was a professor of mathematics at Princeton University, University of California, Davis, and Cornell University. He was also a director of the Mathematical Sciences Research Institute. Early life and education William Thurston was born in Washington, D.C. to Margaret Thurston (), a seamstress, and Paul Thurston, an aeronautical engineer. William Thurston suffered from congenital strabismus as a child, causing issues with depth perception. His mother worked with him as a toddler to reconstruct three-dimensional images from two-dimensional ones. He received his bachelor's degree from New College in 1967 as part of its inaugural class. For his undergraduate thesis, he developed an intuitionist foundation for topology. Following this, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David P
David (; , "beloved one") (traditional spelling), , ''Dāwūd''; grc-koi, Δαυΐδ, Dauíd; la, Davidus, David; gez , ዳዊት, ''Dawit''; xcl, Դաւիթ, ''Dawitʿ''; cu, Давíдъ, ''Davidŭ''; possibly meaning "beloved one". was, according to the Hebrew Bible, the third king of the United Kingdom of Israel. In the Books of Samuel, he is described as a young shepherd and harpist who gains fame by slaying Goliath, a champion of the Philistines, in southern Canaan. David becomes a favourite of Saul, the first king of Israel; he also forges a notably close friendship with Jonathan, a son of Saul. However, under the paranoia that David is seeking to usurp the throne, Saul attempts to kill David, forcing the latter to go into hiding and effectively operate as a fugitive for several years. After Saul and Jonathan are both killed in battle against the Philistines, a 30-year-old David is anointed king over all of Israel and Judah. Following his rise to power, David c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |