|
Pythagorean Trigonometric Identity
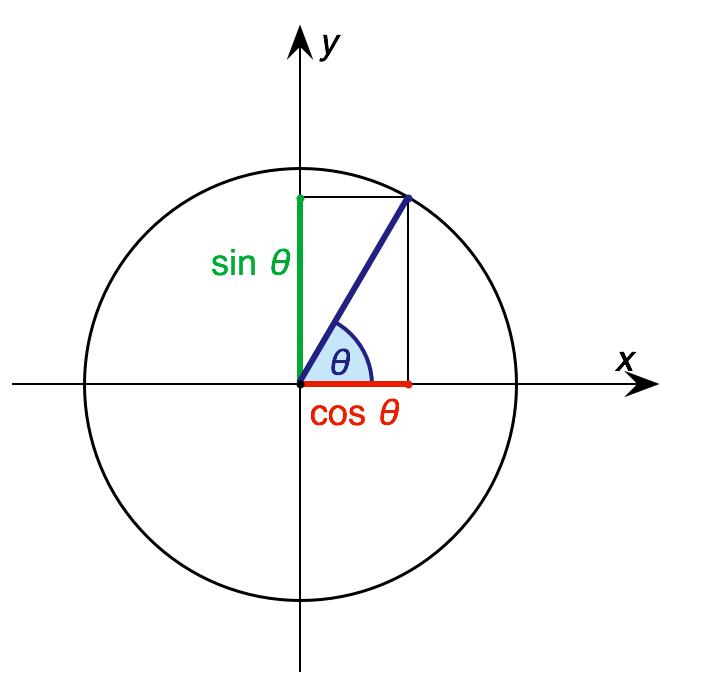
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations between the sine and cosine functions. The identity is :\sin^2 \theta + \cos^2 \theta = 1. As usual, \sin^2 \theta means (\sin\theta)^2. Proofs and their relationships to the Pythagorean theorem Proof based on right-angle triangles Any similar triangles have the property that if we select the same angle in all of them, the ratio of the two sides defining the angle is the same regardless of which similar triangle is selected, regardless of its actual size: the ratios depend upon the three angles, not the lengths of the sides. Thus for either of the similar right triangles in the figure, the ratio of its horizontal side to its hypotenuse is the same, namely . The elementary definitions of the sine and cosine functions in terms of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity (mathematics)
In mathematics, an identity is an equality (mathematics), equality relating one mathematical expression ''A'' to another mathematical expression ''B'', such that ''A'' and ''B'' (which might contain some variable (mathematics), variables) produce the same value for all values of the variables within a certain domain of discourse. In other words, ''A'' = ''B'' is an identity if ''A'' and ''B'' define the same function (mathematics), functions, and an identity is an equality between functions that are differently defined. For example, (a+b)^2 = a^2 + 2ab + b^2 and \cos^2\theta + \sin^2\theta =1 are identities. Identities are sometimes indicated by the triple bar symbol instead of , the equals sign. Formally, an identity is a universally quantified equality. Common identities Algebraic identities Certain identities, such as a+0=a and a+(-a)=0, form the basis of algebra, while other identities, such as (a+b)^2 = a^2 + 2ab +b^2 and a^2 - b^2 = (a+b)(a-b), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Functions And Their Reciprocals On The Unit Circle
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle measur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Plot
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point, as functions of one or several variables called parameters. In the case of a single parameter, parametric equations are commonly used to express the trajectory of a moving point, in which case, the parameter is often, but not necessarily, time, and the point describes a curve, called a parametric curve. In the case of two parameters, the point describes a surface, called a parametric surface. In all cases, the equations are collectively called a parametric representation, or parametric system, or parameterization (also spelled parametrization, parametrisation) of the object. For example, the equations \begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where is the parameter: A point is on the unit circle if and only if there is a value of such that these two equations generate that point. Sometimes the parametric equations f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power expands into a polynomial with terms of the form , where the exponents and are nonnegative integers satisfying and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in each term is known as the binomial coefficient or (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where gives the number of different combinations (i.e. subsets) of elements that can be chosen from an -element set. Therefore is usually pronounced as " choose ". Statement According to the theorem, the expansion of any nonnegative integer power of the binomial is a sum of the form (x+y)^n = x^n y^0 + x^ y^1 + x^ y^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Term
In mathematics, a constant term (sometimes referred to as a free term) is a term in an algebraic expression that does not contain any variables and therefore is constant. For example, in the quadratic polynomial, :x^2 + 2x + 3,\ The number 3 is a constant term. After like terms are combined, an algebraic expression will have at most one constant term. Thus, it is common to speak of the quadratic polynomial :ax^2+bx+c,\ where x is the variable, as having a constant term of c. If the constant term is 0, then it will conventionally be omitted when the quadratic is written out. Any polynomial written in standard form has a unique constant term, which can be considered a coefficient of x^0. In particular, the constant term will always be the lowest degree term of the polynomial. This also applies to multivariate polynomials. For example, the polynomial :x^2+2xy+y^2-2x+2y-4\ has a constant term of −4, which can be considered to be the coefficient of x^0y^0, where the va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an Circular arc, arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless unit, dimensionless SI derived unit,: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units." defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as . Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing. Definition One radian is defined as the angle at the center of a circle in a plane that wikt:subtend, subtends an arc whose length equals the radius of the circle. More generally, the magnit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Series
In mathematics, a power series (in one variable) is an infinite series of the form \sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a constant called the ''center'' of the series. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function. In many situations, the center ''c'' is equal to zero, for instance for Maclaurin series. In such cases, the power series takes the simpler form \sum_^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + \dots. The partial sums of a power series are polynomials, the partial sums of the Taylor series of an analytic function are a sequence of converging polynomial approximations to the function at the center, and a converging power series can be seen as a kind of generalized polynom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of "dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Sine
Periodicity or periodic may refer to: Mathematics * Bott periodicity theorem, addresses Bott periodicity: a modulo-8 recurrence relation in the homotopy groups of classical groups * Periodic function, a function whose output contains values that repeat periodically * Periodic mapping Physical sciences * Periodic table of chemical elements * Periodic trends, relative characteristics of chemical elements observed * Redshift periodicity, astronomical term for redshift quantization Other uses * Fokker periodicity blocks, which mathematically relate musical intervals * Periodic acid, a compound of iodine * Principle of periodicity, a concept in generally accepted accounting principles * Quasiperiodicity, property of a system that displays irregular periodicity See also * Aperiodic (other) * Cycle (other) * Frequency (other) * Period (other) * Periodical * Seasonality In time series data, seasonality refers to the trends that occur at spec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trig Functions On Unit Circle
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic period, Hellenistic world during the 3rd century BC from applications of geometry to Astronomy, astronomical studies. The Greeks focused on the Ptolemy's table of chords, calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identity (mathematics), identities. These List of trigonometric identities, trigonometric identities are commonly used for rewriting trigonometrical expression (mathematics), expressions with the aim to simplify an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosecant
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |