|
Polar Motion
Polar motion of the Earth is the motion of the Earth's rotation, Earth's rotational axis relative to its Earth's crust, crust. This is measured with respect to a reference frame in which the solid Earth is fixed (a so-called ''Earth-centered, Earth-fixed'' or ECEF reference frame). This variation is a few meters on the surface of the Earth. Analysis Polar motion is defined relative to a conventionally defined reference axis, the CIO (Conventional International Origin), being the pole's average location over the year 1900. It consists of three major components: a free oscillation called Chandler wobble with a period of about 435 days, an annual oscillation, and an irregular drift in the direction of the 80th Meridian (geography), meridian west, which has lately been less extremely west. Causes The slow drift, about 20 m since 1900, is partly due to motions in the Earth's core and mantle, and partly to the redistribution of water mass as the Greenland ice sheet melts, and to iso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Milliarcseconds
A minute of arc, arcminute (abbreviated as arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of a degree. Since one degree is of a turn, or complete rotation, one arcminute is of a turn. The nautical mile (nmi) was originally defined as the arc length of a minute of latitude on a spherical Earth, so the actual Earth's circumference is very near . A minute of arc is of a radian. A second of arc, arcsecond (abbreviated as arcsec), or arc second, denoted by the symbol , is a unit of angular measurement equal to of a minute of arc, of a degree, of a turn, and (about ) of a radian. These units originated in Babylonian astronomy as sexagesimal (base 60) subdivisions of the degree; they are used in fields that involve very small angles, such as astronomy, optometry, ophthalmology, optics, navigation, land surveying, and marksmanship. To express even smaller angles, standard SI prefixes can be employed; the milliarcsec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Geodesy
{{Space-stub ...
Space geodesy is geodesy by means of sources external to Earth, mainly artificial satellites (in satellite geodesy) but also quasars (in very-long-baseline interferometry, VLBI), visible stars (in stellar triangulation), and the retroreflectors on the Moon (in lunar laser ranging, LLR). See also * Astronomical geodesy Geodesy Geodesy Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Precession Of The Equinoxes
In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's Rotation around a fixed axis, rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism. In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years.Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) ''Explanatory Supplement to the Astronomical Almanac''. Sausalito: University Science Books. p. 99. This is similar to the precession of a spinning top, with the axis tracing out a pair of Cone (geometry), cones joined at their Apex (geometry), apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis—astronomical nutation, nutation and polar motion—are much smaller in magnitude ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nutation
Nutation () is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behaviour of a mechanism. In an appropriate reference frame it can be defined as a change in the second Euler angle. If it is not caused by forces external to the body, it is called free nutation or Euler nutation (after Leonhard Euler). A pure nutation is a movement of a rotational axis such that the first Euler angle is constant. Therefore it can be seen that the circular red arrow in the diagram indicates the combined effects of precession and nutation, while nutation in the absence of precession would only change the tilt from vertical (second Euler angle). However, in spacecraft dynamics, precession (a change in the first Euler angle) is sometimes referred to as nutation. In a rigid body If a top is set at a tilt on a horizontal surface and spun rapidly, its rotational axis starts precess ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geoid
The geoid ( ) is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents (such as might be approximated with very narrow hypothetical canals). According to Carl Friedrich Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century. The geoid is often expressed as a geoid undulation or geoidal height above a given reference ellipsoid, which is a slightly flattene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth's Rotation Axis
In astronomy, axial tilt, also known as obliquity, is the angle between an object's rotational axis and its orbital axis, which is the line perpendicular to its orbital plane; equivalently, it is the angle between its equatorial plane and orbital plane. It differs from orbital inclination. At an obliquity of 0 degrees, the two axes point in the same direction; that is, the rotational axis is perpendicular to the orbital plane. The rotational axis of Earth, for example, is the imaginary line that passes through both the North Pole and South Pole, whereas the Earth's orbital axis is the line perpendicular to the imaginary plane through which the Earth moves as it revolves around the Sun; the Earth's obliquity or axial tilt is the angle between these two lines. Over the course of an orbital period, the obliquity usually does not change considerably, and the orientation of the axis remains the same relative to the background of stars. This causes one pole to be pointed more to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beat Frequency
In acoustics, a beat is an interference pattern between two sounds of slightly different frequencies, ''perceived'' as a periodic variation in volume whose rate is the difference of the two frequencies. With tuning instruments that can produce sustained tones, beats can be readily recognized. Tuning two tones to a unison will present a peculiar effect: when the two tones are close in pitch but not identical, the difference in frequency generates the beating. The volume varies as in a tremolo as the sounds alternately interfere constructively and destructively. As the two tones gradually approach unison, the beating slows down and may become so slow as to be imperceptible. As the two tones get further apart, their beat frequency starts to approach the range of human pitch perception, the beating starts to sound like a note, and a combination tone is produced. Mathematics and physics of beat tones This phenomenon is best known in acoustics or music, though it can be found in any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seth Carlo Chandler
Seth Carlo Chandler, Jr. (September 16, 1846 – December 31, 1913) was an American astronomer, geodesist, and actuary. He was born in Boston, Massachusetts to Seth Carlo and Mary (née Cheever) Chandler. During his last year in high school he performed mathematical computations for Benjamin Peirce, of the Harvard College Observatory. After graduating, he became the assistant of Benjamin A. Gould. Gould was director of the Longitude Department of the United States Coast Survey, a United States Government agency responsible for geodetic surveys. When Gould left to become director of the national observatory in Argentina, Chandler also left and became an actuary. However, he continued to work in astronomy as an amateur affiliated with Harvard College Observatory. Chandler married Caroline Margaret Herman on October 20th, 1870. They were married for 47 years before Seth Carlo Chandler's death in 1913 and had several daughters together. Chandler is best remembered for his r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Radius
Earth radius (denoted as ''R''🜨 or ''R''E) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid (an oblate ellipsoid), the radius ranges from a maximum (equatorial radius, denoted ''a'') of about to a minimum (polar radius, denoted ''b'') of nearly . A globally-average value is usually considered to be with a 0.3% variability (±10 km) for the following reasons. The International Union of Geodesy and Geophysics (IUGG) provides three reference values: the ''mean radius'' (''R'') of three radii measured at two equator points and a pole; the ''authalic radius'', which is the radius of a sphere with the same surface area (''R''); and the ''volumetric radius'', which is the radius of a sphere having the same volume as the ellipsoid (''R''). All three values are about . Other ways to define and measure the Earth's radius involve either the spheroid's radius of curvature or the actual topography. A few ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
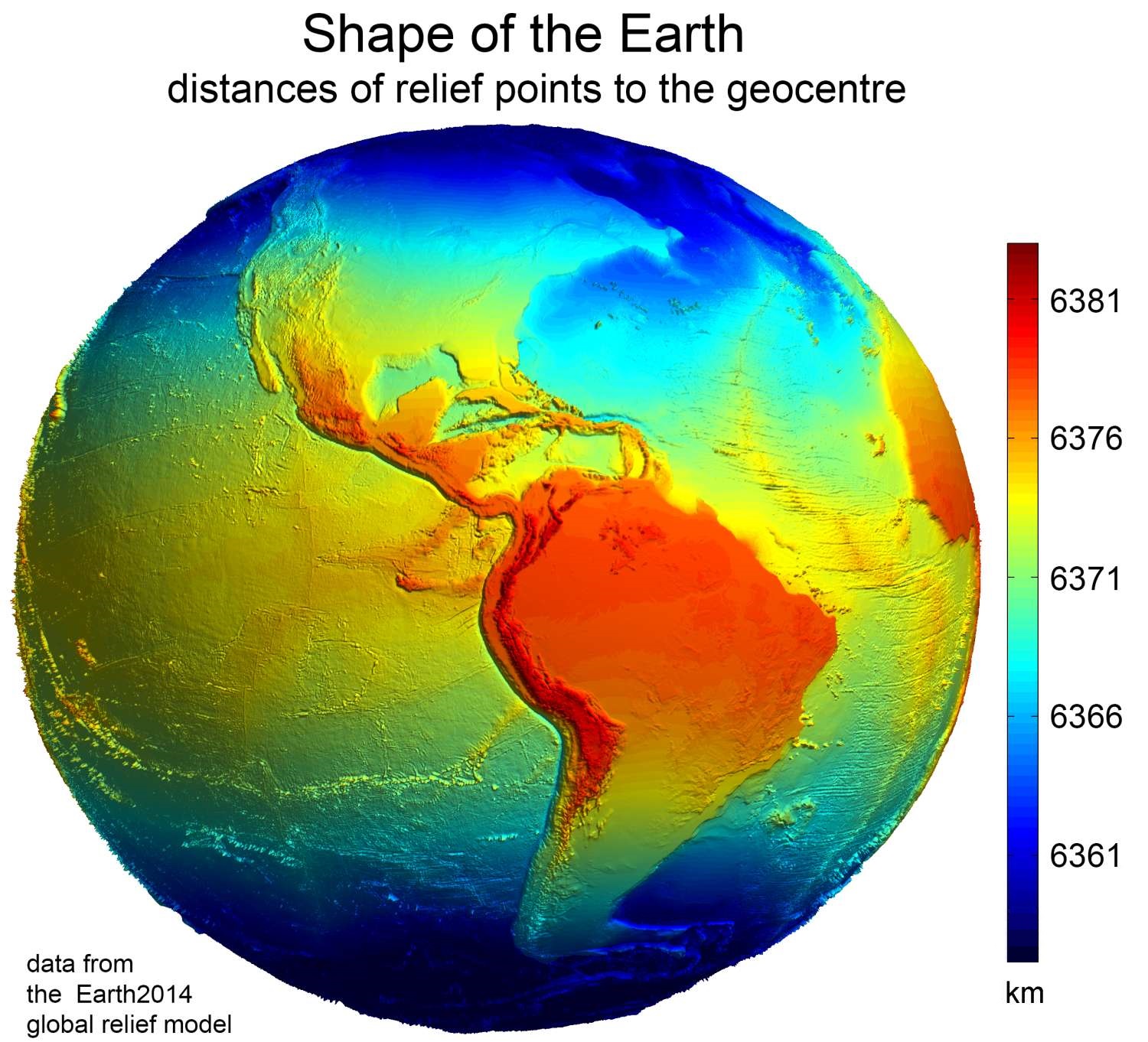
Earth's Figure
In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is satisfactory for geography, astronomy and many other purposes. Several models with greater accuracy (including ellipsoid) have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns. Motivation Earth's topographic surface is apparent with its variety of land forms and water areas. This topographic surface is generally the concern of topographers, hydrographers, and geophysicists. While it is the surface on which Earth measurements are made, mathematically modeling it while taking the irregularities into account would be extremely complicated. The Pythagorean concept of a spherical Earth offers a simple surface that is easy to deal with mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Length
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the most basic formulation of arc length for a vector valued curve (thought of as the trajectory of a particle), the arc length is obtained by integrating speed, the magnitude of the velocity vector over the curve with respect to time. Thus the length of a continuously differentiable curve (x(t),y(t)), for a\le t\le b, in the Euclidean plane is given as the integral L = \int_a^b \sqrt\,dt, (because \sqrt is the magnitude of the velocity vector (x'(t),y'(t)), i.e., the particle's speed). The defining integral of arc length does not always have a closed-form expression, and numerical integration may be used instead to obtain numerical values of arc length. Determining the length of an irregular arc segment by approximating the arc segment as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |