|
Poincaré And The Three-Body Problem
''Poincaré and the Three-Body Problem'' is a monograph in the history of mathematics on the work of Henri Poincaré on the three-body problem in celestial mechanics. It was written by June Barrow-Green, as a revision of her 1993 doctoral dissertation, and published in 1997 by the American Mathematical Society and London Mathematical Society as Volume 11 in their shared History of Mathematics series (). The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries. Topics The three-body problem concerns the motion of three bodies interacting under Newton's law of universal gravitation, and the existence of orbits for those three bodies that remain stable over long periods of time. This problem has been of great interest mathematically since Newton's formulation of the laws of gravity, in particular with respect to the joint motion of the sun, earth, and moon. The centerpiece of ''Poincaré and the Thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
June Barrow-Green
June Barrow-Green (born 1953) is a professor of History of Mathematics at the Open University and a visiting professor at the London School of Economics. Education Barrow-Green obtained a BSc Hons in Mathematics in 1986 and an MSc in Mathematical Physics in 1989, both from King's College London. In 1993 she gained a PhD in mathematics from the Open University, under supervision of Jeremy Gray, on ''Poincaré and the Three Body Problem''. Career From 1993 to the present Barrow-Green has worked at the Open University, receiving a professorship in 2015. From 2003 to 2005 she was president of the British Society for the History of Mathematics. From 2007 to 2018 she was an elected member of the Council of the London Mathematical Society and during that period she served as the Librarian for the society. In 2014 Barrow-Green was awarded the first Chandler Davis Prize for Expository Excellence for her article ''An American Goes to Europe: Three Letters from Oswald Veblen to Georg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel Bernoulli
Daniel Bernoulli ( ; ; – 27 March 1782) was a Swiss people, Swiss-France, French mathematician and physicist and was one of the many prominent mathematicians in the Bernoulli family from Basel. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics. His name is commemorated in the Bernoulli's principle, a particular example of the conservation of energy, which describes the mathematics of the mechanism underlying the operation of two important technologies of the 20th century: the carburetor and the aeroplane wing. Early life Daniel Bernoulli was born in Groningen (city), Groningen, in the Netherlands, into a Bernoulli family, family of distinguished mathematicians.Murray Rothbard, Rothbard, MurrayDaniel Bernoulli and the Founding of Mathematical Economics, ''Mises Institute'' (excerpted from ''An Austrian Perspective on the History of Economic Thought'') The Bernou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homoclinic Orbit
In the study of dynamical systems, a homoclinic orbit is a path through phase space which joins a saddle equilibrium point to itself. More precisely, a homoclinic orbit lies in the intersection of the stable manifold and the unstable manifold of an equilibrium. It is a heteroclinic orbit–a path between any two equilibrium points–in which the endpoints are one and the same. Consider the continuous dynamical system described by the ordinary differential equation :\dot x=f(x) Suppose there is an equilibrium at x=x_0, then a solution \Phi(t) is a homoclinic orbit if :\Phi(t)\rightarrow x_0\quad \mathrm\quad t\rightarrow\pm\infty If the phase space has three or more dimensions, then it is important to consider the topology of the unstable manifold of the saddle point. The figures show two cases. First, when the stable manifold is topologically a cylinder, and secondly, when the unstable manifold is topologically a Möbius strip; in this case the homoclinic orbit is called ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gösta Mittag-Leffler
Magnus Gustaf "Gösta" Mittag-Leffler (16 March 1846 – 7 July 1927) was a Sweden, Swedish mathematician. His mathematical contributions are connected chiefly with the theory of functions that today is called complex analysis. He founded the prestigious mathematical periodical ''Acta Mathematica'' and was its editor for 40 years. He took great trouble in procuring Sofia Kovalevskaya a position of full professor of mathematics in Stockholm University. Mittag-Leffler was also responsible for inducing the Nobel Prize, Nobel committee to recognize and award Marie Curie as an equal contributor to the discoveries "on the radiation phenomena" along with her husband Pierre Curie. After World War I, Mittag-Leffler gave his estate in Djursholm and its remarkable library of books on mathematics to the Royal Swedish Academy of Sciences; it became the foundation of the modern ''Mittag-Leffler Institute''. Biography Early years and education Mittag-Leffler was born in Stockholm and becam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acta Arithmetica
''Acta Arithmetica'' is a scientific journal of mathematics publishing papers on number theory. It was established in 1935 by Salomon Lubelski and Arnold Walfisz. The journal is published by the Institute of Mathematics of the Polish Academy of Sciences. References External links Online archives (Library of Science, Issues: 1935–2000) 1935 establishments in Poland Number theory journals Academic journals established in 1935 Polish Academy of Sciences academic journals Biweekly journals Academic journals associated with learned and professional societies {{math-journal-stub English-language journals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
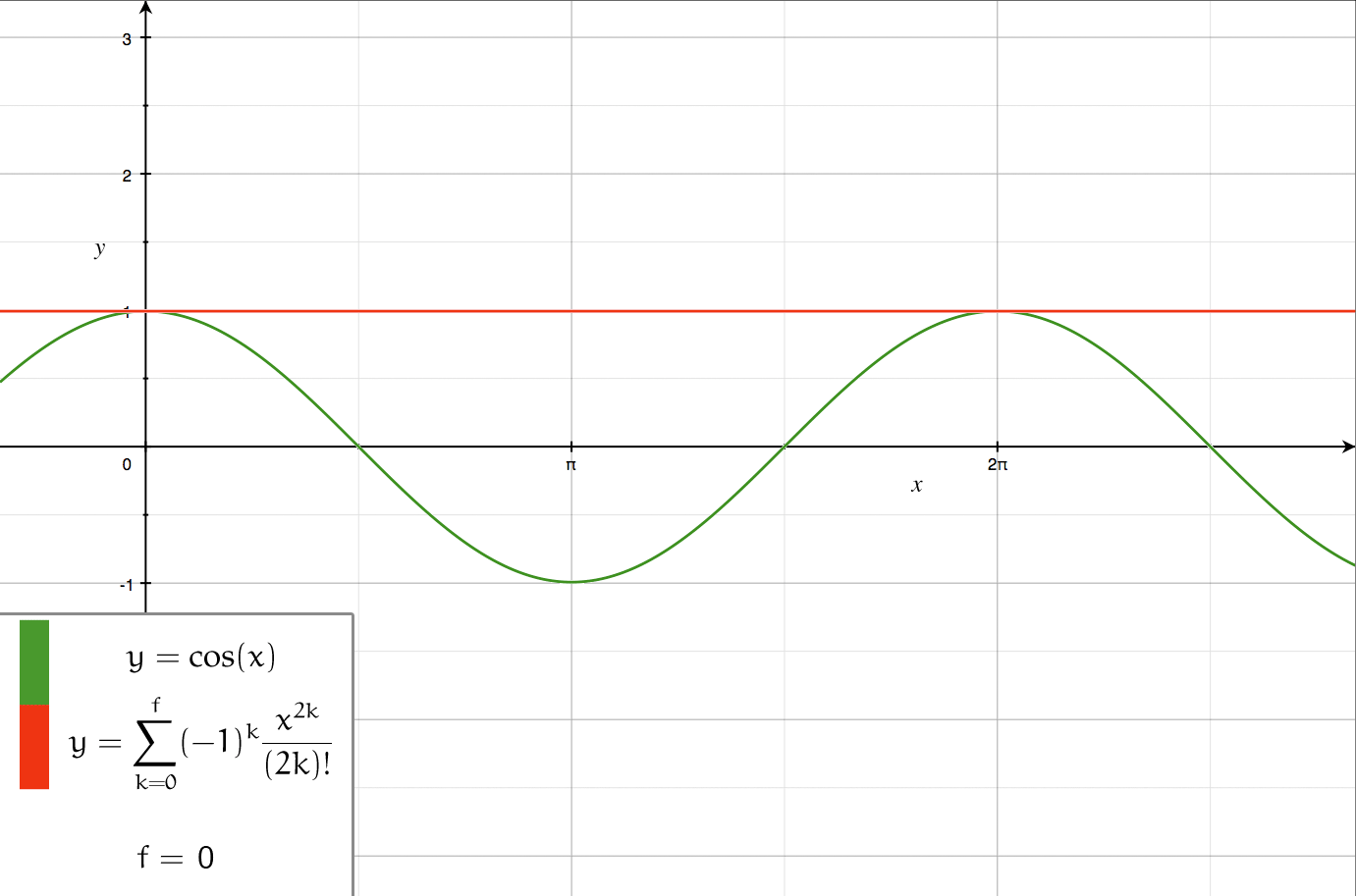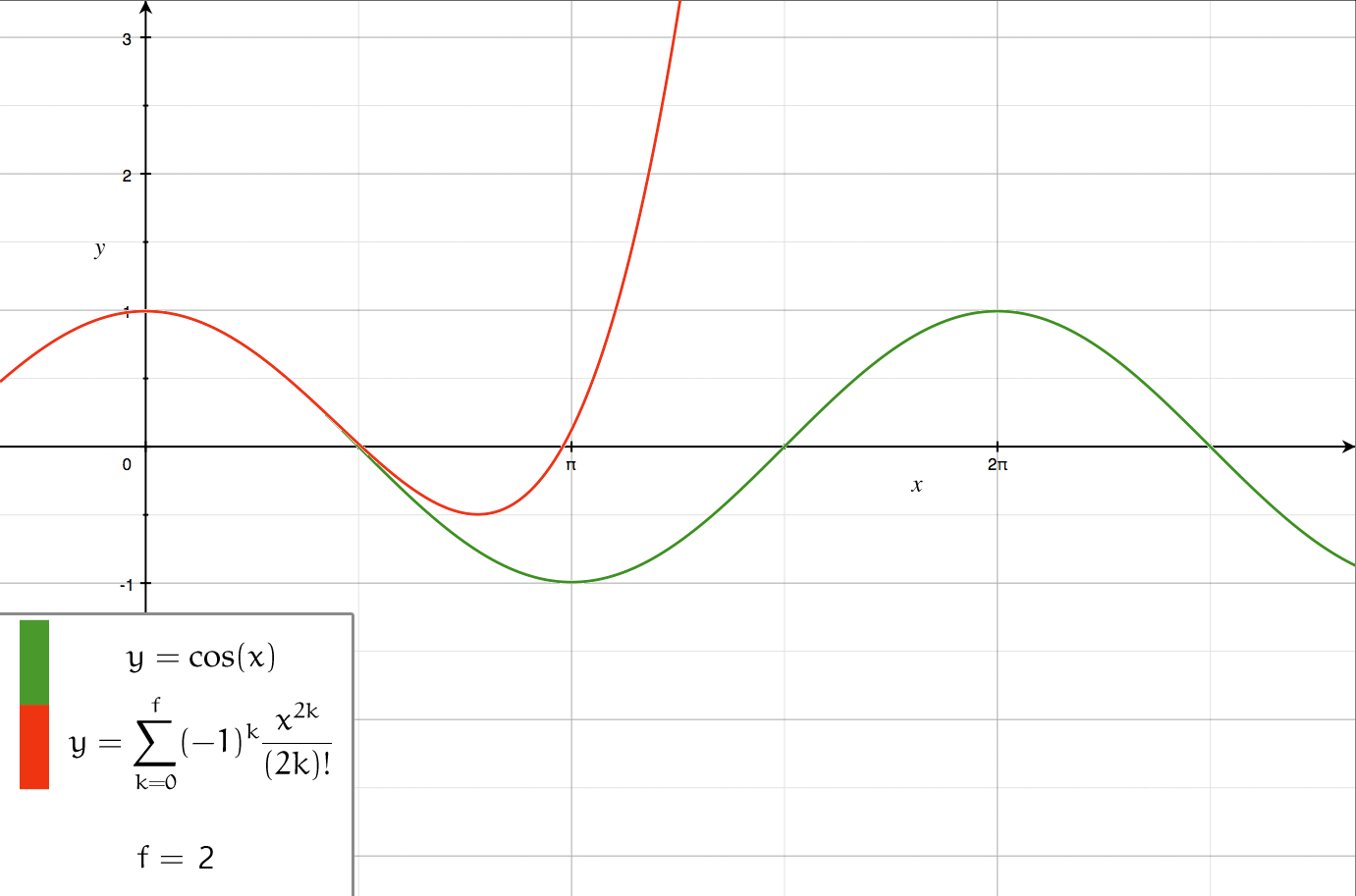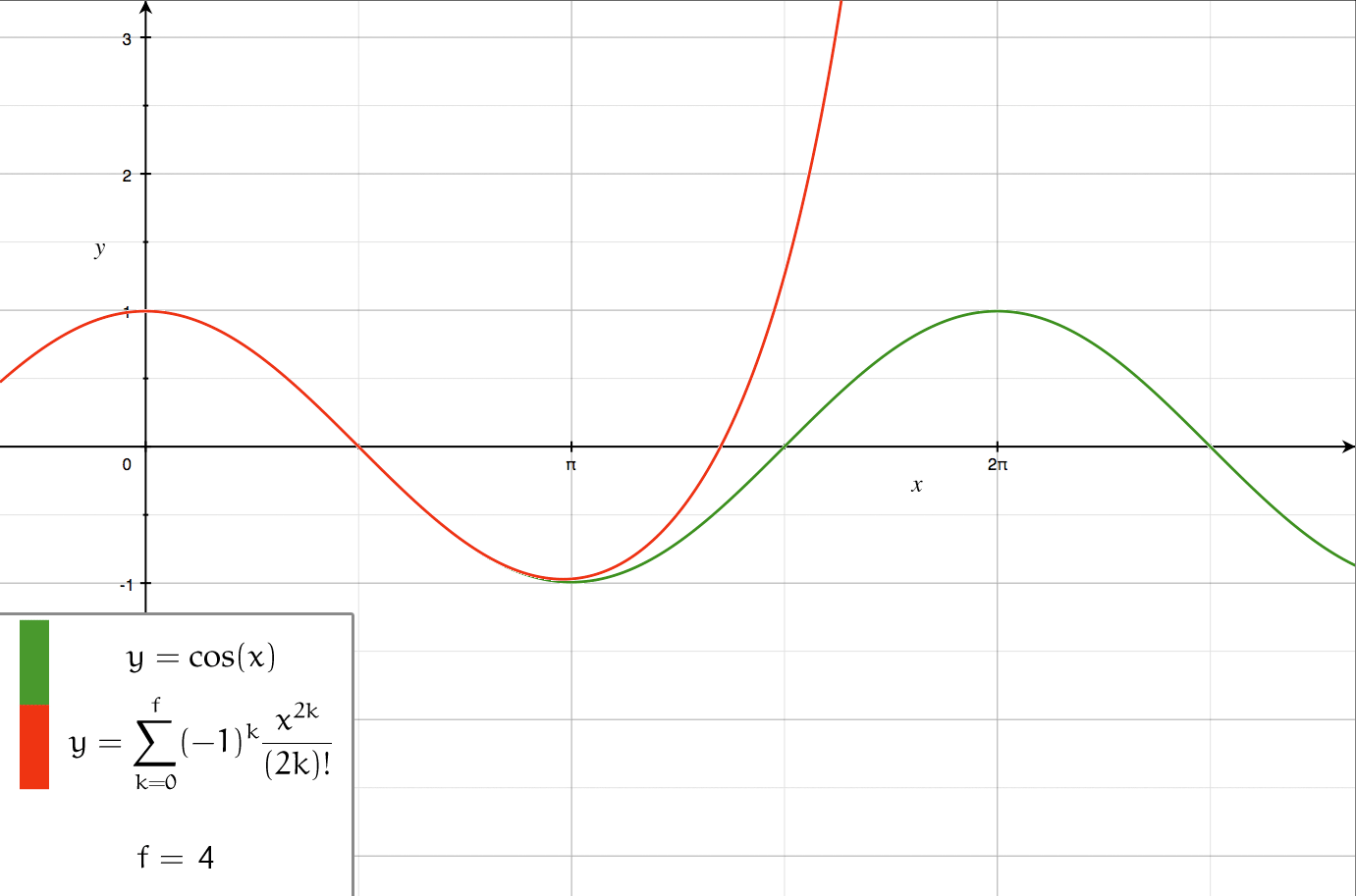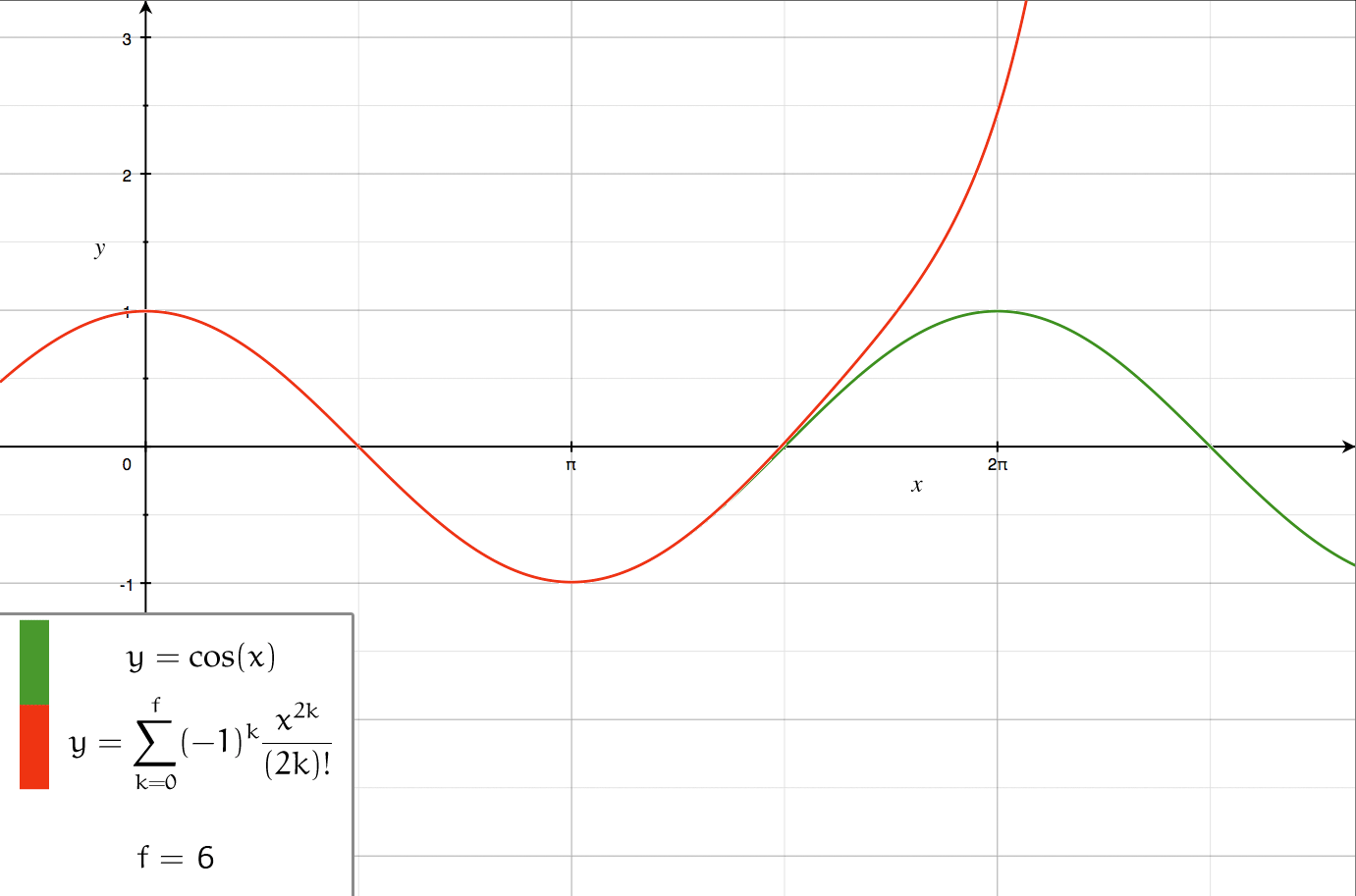
Series Expansion
In mathematics, a series expansion is a technique that expresses a Function (mathematics), function as an infinite sum, or Series (mathematics), series, of simpler functions. It is a method for calculating a Function (mathematics), function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''Series (mathematics), series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. Taylor series A ''Taylor series'' is a power ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George William Hill
George William Hill (March 3, 1838 – April 16, 1914) was an American astronomer and mathematician. Working independently and largely in isolation from the wider scientific community, he made major contributions to celestial mechanics and to the theory of ordinary differential equations. The importance of his work was explicitly acknowledged by Henri Poincaré in 1905. In 1909 Hill was awarded the Royal Society's Copley Medal, "on the ground of his researches in mathematical astronomy". Hill is remembered for the Hill differential equation, along with the Hill sphere. Early life and education Hill was born in New York City to painter and engraver John William Hill and his wife, Catherine Smith. He moved to West Nyack with his family when he was eight years old. After high school, Hill attended Rutgers College, where he became interested in mathematics. At Rutgers, Hill came under the influence of professor Theodore Strong, who was a friend of pioneering US mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anders Lindstedt
Anders Lindstedt (27 June 1854 – 16 May 1939) was a Swedish mathematician, astronomer, and actuarial scientist, known for the Lindstedt-Poincaré method. Life and work Lindstedt was born in a small village in the district of Sundborns, Dalecarlia a province in central Sweden.Hvar 8 dag, 10:de Årg, No 11, 13 december 1908, sid. 162'.Memoir Anders Lindstedt 27 June 1854-16 May 1939, Journal of the Institute of Actuaries, 70 (1939) p. 269/ref> He obtained a PhD from the University of Lund aged 32 and was subsequently appointed as a lecturer in astronomy. He later went on to a position at the University of Dorpat (then belonging to Russia, now University of Tartu in Estonia) where he worked for around seven years on theoretical astronomy. He combined practical astronomy with an interest in theory, developing especially an interest in the three-body problem This work was to influence Poincaré whose work on the three-body problem led to the discovery that there can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles-Eugène Delaunay
Charles-Eugène Delaunay (; 9 April 1816 – 5 August 1872) was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics. Life Born in Lusigny-sur-Barse, France, to Jacques-Hubert Delaunay and Catherine Choiselat, Delaunay studied under Jean-Baptiste Biot at the Sorbonne. He worked on the mechanics of the Moon as a special case of the three-body problem. He published two volumes on the topic, each of 900 pages in length, in 1860 and 1867. The work hints at chaos in the system, and clearly demonstrates the problem of so-called "small denominators" in perturbation theory. His infinite series expression for finding the position of the Moon converged too slowly to be of practical use but was a catalyst in the development of functional analysisO'Connor & Edmund and computer algebra. Delaunay became director of the Paris Observatory in 1870 but drowned in a boating accident near Cherbourg, Fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexis Clairaut
Alexis Claude Clairaut (; ; 13 May 1713 – 17 May 1765) was a French mathematician, astronomer, and geophysicist. He was a prominent Newtonian whose work helped to establish the validity of the principles and results that Isaac Newton, Sir Isaac Newton had outlined in the ''Principia Mathematica Philosophiae Naturalis, Principia'' of 1687. Clairaut was one of the key figures in the expedition to Sápmi, Lapland that helped to confirm Newton's theory for the figure of the Earth. In that context, Clairaut worked out a mathematical result now known as "Clairaut's theorem (gravity), Clairaut's theorem". He also tackled the gravitational three-body problem, being the first to obtain a satisfactory result for the apsidal precession of the Moon's orbit. In mathematics he is also credited with Clairaut's equation and Clairaut's relation. Biography Childhood and early life Clairaut was born in Paris, France, to Jean-Baptiste and Catherine Petit Clairaut. The couple had 20 children, howe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |