|
Periodic Table Of Shapes
The periodic table of mathematical shapes is the popular name given to a project to classify Fano varieties. The project was devised by Professor Alessio Corti, from the Department of Mathematics at Imperial College London. It aims to categorise all three-, four- and five-dimensional shapes into a single table, analogous to the periodic table of chemical elements. It is meant to hold the equations that describe each shape and, through this, mathematicians and other scientists expect to develop a better understanding of the shapes’ geometric properties and relations. The project has already won the Philip Leverhulme Prize—worth £70,000—from the Leverhulme Trust, and in 2019 a European Research Council grant. While it is estimated that 500 million shapes can be defined algebraically in four dimensions, they may be decomposable (in the sense of the minimal model program) into as few as a few thousand "building blocks". See also * List of complex and algebraic surfaces *List ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fano Varieties
In algebraic geometry, a Fano variety, introduced by Gino Fano , is an algebraic variety that generalizes certain aspects of complete intersections of algebraic hypersurfaces whose sum of degrees is at most the total dimension of the ambient projective space. Such complete intersections have important applications in geometry and number theory, because they typically admit rational points, an elementary case of which is the Chevalley–Warning theorem. Fano varieties provide an abstract generalization of these basic examples for which rationality questions are often still tractable. Formally, a Fano variety is a complete variety ''X'' whose anticanonical bundle ''K''X* is ample. In this definition, one could assume that ''X'' is smooth over a field, but the minimal model program has also led to the study of Fano varieties with various types of singularities, such as terminal or klt singularities. Recently techniques in differential geometry have been applied to the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alessio Corti
Alessio Corti (born 1965) is a Professor of Mathematics at Imperial College London working in Algebraic Geometry. Corti studied at the University of Pisa and Scuola Normale Superiore in Pisa, where he gained a diploma (Laurea) in 1987. He obtained his PhD in 1992 at the University of Utah under the supervision of János Kollár. As a post-doctoral researcher, he was at the Scuola Normale Superiore in Pisa and at the Mathematical Sciences Research Institute in Berkeley, California. From 1993 to 1996 he was the Dickson Instructor at the University of Chicago and in 1996 became lecturer, later reader, of mathematics at the University of Cambridge. Since 2005 he has been a professor at Imperial College London. In 2002, he was awarded the London Mathematical Society The London Mathematical Society (LMS) is one of the United Kingdom's Learned society, learned societies for mathematics (the others being the Royal Statistical Society (RSS), the Institute of Mathematics and its Ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
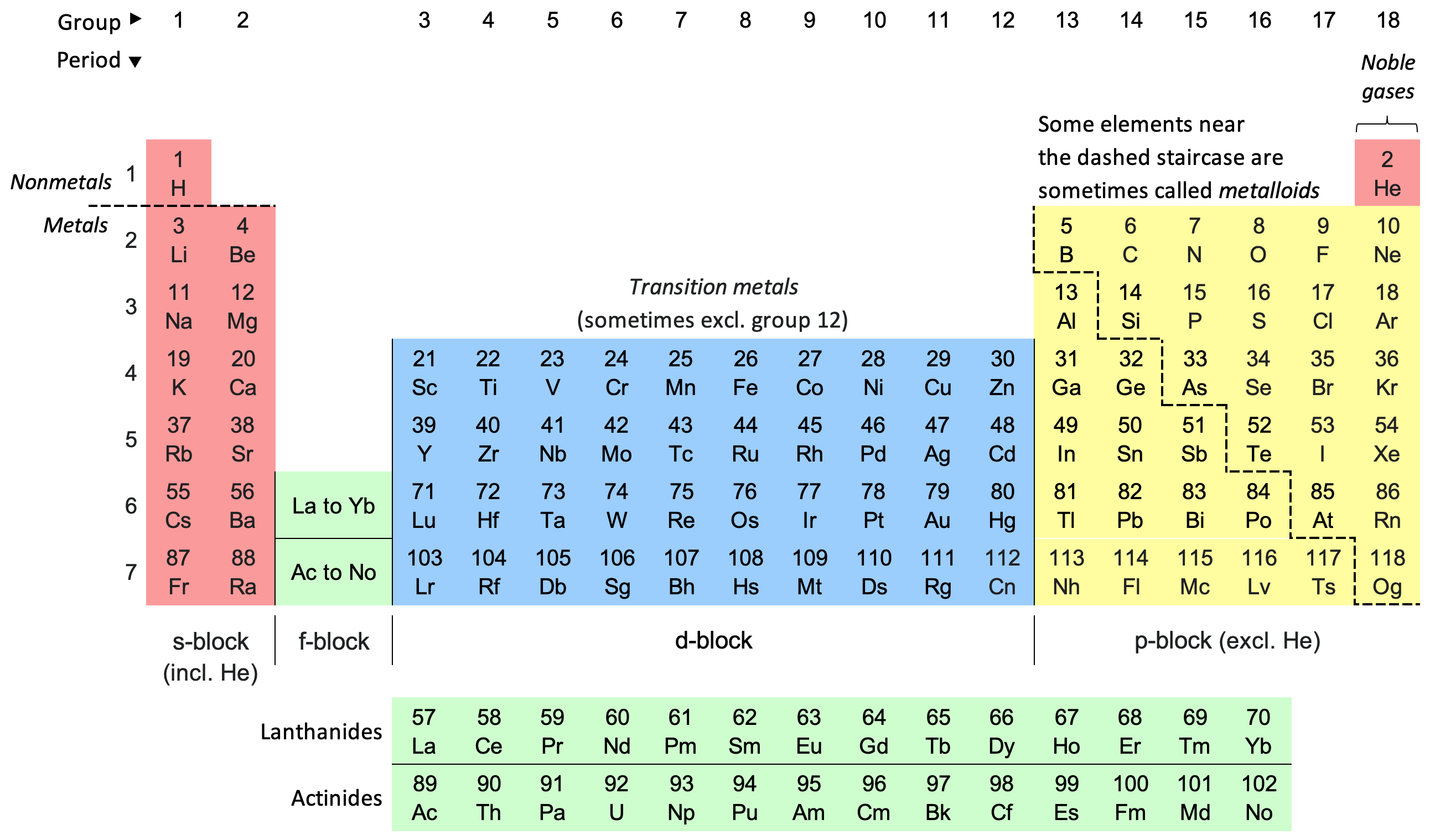
Periodic Table
The periodic table, also known as the periodic table of the elements, is an ordered arrangement of the chemical elements into rows (" periods") and columns (" groups"). It is an icon of chemistry and is widely used in physics and other sciences. It is a depiction of the periodic law, which states that when the elements are arranged in order of their atomic numbers an approximate recurrence of their properties is evident. The table is divided into four roughly rectangular areas called blocks. Elements in the same group tend to show similar chemical characteristics. Vertical, horizontal and diagonal trends characterize the periodic table. Metallic character increases going down a group and from right to left across a period. Nonmetallic character increases going from the bottom left of the periodic table to the top right. The first periodic table to become generally accepted was that of the Russian chemist Dmitri Mendeleev in 1869; he formulated the periodic law as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip Leverhulme Prize
The Philip Leverhulme Prize is awarded by the Leverhulme Trust to recognise the achievement of outstanding researchers whose work has already attracted international recognition and whose future career is exceptionally promising. The prize scheme makes up to thirty awards of £100,000 a year, across a range of academic disciplines. History and criteria The award is named after Philip Leverhulme who died in 2000. He was the grandson of William Leverhulme, and was the third Viscount Leverhulme. The prizes are payable, in instalments, over a period of two to three years. Prizes can be used for any purpose which can advance the prize-holder’s research, with the exception of enhancing the prize-holder’s salary. Nominees must hold either a permanent post or a long-term fellowship in a UK institution of higher education or research that would extend beyond the duration of the Philip Leverhulme Prize. Those otherwise without salary are not eligible to be nominated. Nominees sh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leverhulme Trust
The Leverhulme Trust () is a large national grant-making organisation in the United Kingdom. It was established in 1925 under the will of the 1st Viscount Leverhulme (1851–1925), with the instruction that its resources should be used to cover certain trade charities and support "scholarships for the purposes of research and education." Over time, it has come to focus on the latter aim. The Trust is based in London and is a registered charity under English law. The current Chair of the Trust is Alan Jope CBE. Activities Since its foundation in 1925, the Trust has provided funding for research projects, fellowships, studentships, bursaries and prizes. It operates across all academic disciplines with the intention of supporting individuals in research and professional training. Dispensing over £100 million a year, the Trust is one of the largest providers of research funding in the UK. The Trust places special weight on: * the originality of the projects put to them; * th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
European Research Council
The European Research Council (ERC) is a public body for funding of scientific and technological research conducted within the European Union (EU). Established by the European Commission in 2007, the ERC is composed of an independent Scientific Council, its governing body consisting of distinguished researchers, and an Executive Agency, in charge of the implementation. It forms part of the framework programme of the union dedicated to research and innovation, Horizon 2020, preceded by the Seventh Research Framework Programme (FP7). The ERC budget is over €13 billion from 2014 – 2020 and comes from the Horizon 2020 programme, a part of the European Union's budget. Under Horizon 2020 it is estimated that around 7,000 ERC grantees will be funded and 42,000 team members supported, including 11,000 doctoral students and almost 16,000 post-doctoral researchers. The ERC awards to individuals are widely considered to be either among the most, or else the most prestigious grant for aca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Model Program
In algebraic geometry, the minimal model program is part of the birational classification of algebraic varieties. Its goal is to construct a birational model of any complex projective variety which is as simple as possible. The subject has its origins in the classical birational geometry of surfaces studied by the Italian school, and is currently an active research area within algebraic geometry. Outline The basic idea of the theory is to simplify the birational classification of varieties by finding, in each birational equivalence class, a variety which is "as simple as possible". The precise meaning of this phrase has evolved with the development of the subject; originally for surfaces, it meant finding a smooth variety X for which any birational morphism f\colon X \to X' with a smooth surface X' is an isomorphism. In the modern formulation, the goal of the theory is as follows. Suppose we are given a projective variety X, which for simplicity is assumed non-singular. There are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Complex And Algebraic Surfaces
This is a list of named algebraic surfaces, compact complex surfaces, and families thereof, sorted according to their Kodaira dimension following Enriques–Kodaira classification. Kodaira dimension −∞ Rational surfaces * Projective plane Quadric surfaces *Cone (geometry) *Cylinder *Ellipsoid *Hyperboloid *Paraboloid *Sphere *Spheroid Rational cubic surfaces * Cayley nodal cubic surface, a certain cubic surface with 4 nodes * Cayley's ruled cubic surface * Clebsch surface or Klein icosahedral surface * Fermat cubic * Monkey saddle * Parabolic conoid * Plücker's conoid * Whitney umbrella Rational quartic surfaces * Châtelet surfaces * Dupin cyclides, inversions of a cylinder, torus, or double cone in a sphere * Gabriel's horn * Right circular conoid * Roman surface or Steiner surface, a realization of the real projective plane in real affine space * Tori, surfaces of revolution generated by a circle about a coplanar axis Other rational surfaces in space * B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Surfaces
This is a list of surface (mathematics), surfaces in mathematics. They are divided into minimal surfaces, ruled surfaces, non-orientable surfaces, quadrics, pseudospherical surfaces, algebraic surfaces, and other types of surfaces. Minimal surfaces * Catalan's minimal surface * Costa's minimal surface * Catenoid * Enneper surface * Gyroid * Helicoid * Lidinoid * Riemann's minimal surface * Saddle tower * Scherk surface * Schwarz minimal surface * Triply periodic minimal surface Ruled surfaces * Catalan surface * Right conoid * Conical surface * Helicoid * Developable rollers (sphericon, oloid) * Hyperboloid of one sheet (doubly ruled) * Hyperbolic paraboloid (doubly ruled) * Rational normal scroll * Regulus (geometry), Regulus Non-orientable surfaces *Klein bottle *Real projective plane **Cross-cap **Roman surface **Boy's surface Quadrics *Sphere *Spheroid **Oblate spheroid **Prolate spheroid *Ellipsoid *Cone (geometry) *Hyperboloid of one sheet *Hyperboloid of two sheets *H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lists Of Shapes
Lists of shapes cover different types of geometric shape and related topics. They include mathematics topics and other lists of shapes, such as shapes used by drawing or teaching tools. Mathematics * List of mathematical shapes * List of two-dimensional geometric shapes ** List of triangle topics ** List of circle topics * List of curves * List of surfaces * List of polygons, polyhedra and polytopes ** List of regular polytopes and compounds Elsewhere * Solid geometry, including table of major three-dimensional shapes * Box-drawing character * Cuisenaire rods (learning aid) * Geometric shape * Geometric Shapes (Unicode block) Geometric Shapes is a Unicode block of 96 symbols at code point range U+25A0–25FF. Font coverage Font sets like Code2000 and the DejaVu fonts, DejaVu family include coverage for each of the glyphs in the Geometric Shapes range. GNU Unifont, ... * Glossary of shapes with metaphorical names * List of symbols * Pattern Blocks (learning aid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Mathematical Shapes
Following is a list of shapes studied in mathematics. Algebraic curves *Cubic plane curve *Quartic plane curve *Fractal Rational curves Degree 2 *Conic sections *Unit circle *Unit hyperbola Degree 3 * Folium of Descartes *Cissoid of Diocles * Conchoid of de Sluze * Right strophoid * Semicubical parabola * Serpentine curve * Trident curve * Trisectrix of Maclaurin *Tschirnhausen cubic *Witch of Agnesi Degree 4 * Ampersand curve *Bean curve *Bicorn * Bow curve * Bullet-nose curve * Cruciform curve *Deltoid curve * Devil's curve *Hippopede * Kampyle of Eudoxus *Kappa curve * Lemniscate of Booth *Lemniscate of Gerono *Lemniscate of Bernoulli *Limaçon **Cardioid **Limaçon trisectrix * Trifolium curve Degree 5 * Quintic of l'Hospital Degree 6 *Astroid *Atriphtaloid * Nephroid * Quadrifolium Families of variable degree * Epicycloid *Epispiral *Epitrochoid *Hypocycloid * Lissajous curve * Poinsot's spirals * Rational normal curve * Rose curve Curves of genus one * Bicuspid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Two-dimensional Geometric Shapes
This is a list of two-dimensional geometric shapes in Euclidean geometry, Euclidean and other geometry, geometries. For mathematical objects in more dimensions, see list of mathematical shapes. For a broader scope, see list of shapes. Generally composed of straight line segments * Angle * Balbis * Concave polygon * Constructible polygon * Convex polygon * Cyclic polygon * Equiangular polygon * Equilateral polygon * Penrose tile * Polyform * Regular polygon * Simple polygon * Tangential polygon Polygons with specific numbers of sides * Triangle – 3 sides ** Acute triangle ** Equilateral triangle ** Heptagonal triangle ** Isosceles triangle *** Golden triangle (mathematics), Golden Triangle ** Obtuse triangle ** Rational triangle ** Heronian triangle *** Pythagorean triangle *** Isosceles heronian triangle *** Primitive Heronian triangle ** Right triangle *** 30-60-90 triangle *** Isosceles right triangle *** Kepler triangle ** Scalene triangle * Quadrilateral – 4 sides **Cycl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |