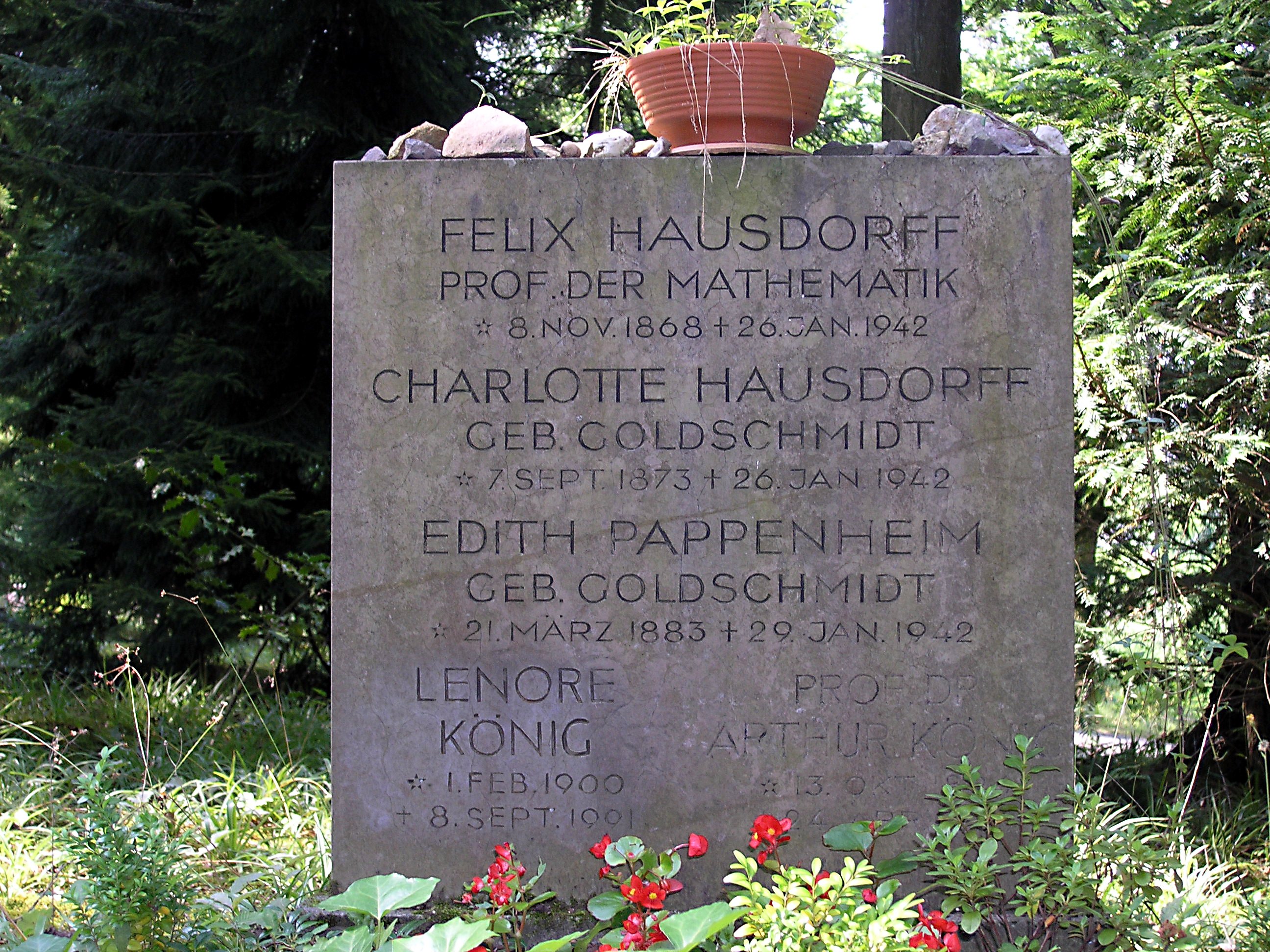|
Path-connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a subspace of X. Some related but stronger conditions are path connected, simply connected, and n-connected. Another related notion is locally connected, which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice. For a topological space X the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-connected Space
In algebraic topology, homotopical connectivity is a property describing a topological space based on the dimension of its holes. In general, low homotopical connectivity indicates that the space has at least one low-dimensional hole. The concept of ''n''-connectedness generalizes the concepts of path-connectedness and simple connectedness. An equivalent definition of homotopical connectivity is based on the homotopy groups of the space. A space is ''n''-connected (or ''n''-simple connected) if its first ''n'' homotopy groups are trivial. Homotopical connectivity is defined for maps, too. A map is ''n''-connected if it is an isomorphism "up to dimension ''n,'' in homotopy". Definition using holes All definitions below consider a topological space ''X''. A hole in ''X'' is, informally, a thing that prevents some suitably-placed sphere from continuously shrinking to a point., Section 4.3 Equivalently, it is a sphere that cannot be continuously extended to a ball. Formally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Properties
In topology and related areas of mathematics, a topological property or topological invariant is a property of a topological space that is invariant under homeomorphisms. Alternatively, a topological property is a proper class of topological spaces which is closed under homeomorphisms. That is, a property of spaces is a topological property if whenever a space ''X'' possesses that property every space homeomorphic to ''X'' possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets. A common problem in topology is to decide whether two topological spaces are homeomorphic or not. To prove that two spaces are ''not'' homeomorphic, it is sufficient to find a topological property which is not shared by them. Properties of topological properties A property P is: * Hereditary, if for every topological space (X, \mathcal) and subset S \subseteq X, the subspace \left(S, \mathcal, _S\right) has property P. * Weakly heredit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simply Connected Space
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed into any other such path while preserving the two endpoints in question. Intuitively, this corresponds to a space that has no disjoint parts and no holes that go completely through it, because two paths going around different sides of such a hole cannot be continuously transformed into each other. The fundamental group of a topological space is an indicator of the failure for the space to be simply connected: a path-connected topological space is simply connected if and only if its fundamental group is trivial. Definition and equivalent formulations A topological space X is called if it is path-connected and any loop in X defined by f : S^1 \to X can be contracted to a point: there exists a continuous map F : D^2 \to X such that F restricted to S^1 is f. Here, S^1 and D^2 denotes the unit c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary (topology)
In topology and mathematics in general, the boundary of a subset of a topological space is the set of points in the Closure (topology), closure of not belonging to the Interior (topology), interior of . An element of the boundary of is called a boundary point of . The term boundary operation refers to finding or taking the boundary of a set. Notations used for boundary of a set include \operatorname(S), \operatorname(S), and \partial S. Some authors (for example Willard, in ''General Topology'') use the term frontier instead of boundary in an attempt to avoid confusion with a Manifold#Manifold with boundary, different definition used in algebraic topology and the theory of manifolds. Despite widespread acceptance of the meaning of the terms boundary and frontier, they have sometimes been used to refer to other sets. For example, ''Metric Spaces'' by E. T. Copson uses the term boundary to refer to Felix Hausdorff, Hausdorff's border, which is defined as the intersection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Connected Space
In topology and other branches of mathematics, a topological space ''X'' is locally connected if every point admits a neighbourhood basis consisting of open connected sets. As a stronger notion, the space ''X'' is locally path connected if every point admits a neighbourhood basis consisting of open path connected sets. Background Throughout the history of topology, connectedness and compactness have been two of the most widely studied topological properties. Indeed, the study of these properties even among subsets of Euclidean space, and the recognition of their independence from the particular form of the Euclidean metric, played a large role in clarifying the notion of a topological property and thus a topological space. However, whereas the structure of ''compact'' subsets of Euclidean space was understood quite early on via the Heine–Borel theorem, ''connected'' subsets of \R^n (for ''n'' > 1) proved to be much more complicated. Indeed, while any compact Hausdorff sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. When quantified, A \subseteq B is represented as \forall x \left(x \in A \Rightarrow x \in B\right). One can prove the statement A \subseteq B by applying a proof technique known as the element argument:Let sets ''A'' and ''B'' be given. To prove that A \subseteq B, # suppose that ''a'' is a particular but arbitrarily chosen element of A # show that ''a'' is an element of ''B''. The validity of this technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frigyes Riesz
Frigyes Riesz (, , sometimes known in English and French as Frederic Riesz; 22 January 1880 – 28 February 1956) was a HungarianEberhard Zeidler: Nonlinear Functional Analysis and Its Applications: Linear monotone operators. Springer, 199/ref> mathematician who made fundamental contributions to functional analysis, as did his younger brother Marcel Riesz. Life and career He was born into a Jewish family in Győr, Austria-Hungary and died in Budapest, Hungary. Between 1911 and 1919 he was a professor at the Franz Joseph University in Kolozsvár, Austria-Hungary. The post-WW1 Treaty of Trianon transferred former Austro-Hungarian territory including Kolozsvár to the Kingdom of Romania, whereupon Kolozsvár's name changed to Cluj and the University of Kolozsvár moved to Szeged, Hungary, becoming the University of Szeged. Then, Riesz was the rector and a professor at the University of Szeged, as well as a member of the Hungarian Academy of Sciences. and the Polish Academ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Hausdorff
Felix Hausdorff ( , ; November 8, 1868 – January 26, 1942) was a German mathematician, pseudonym Paul Mongré (''à mogré' (Fr.) = "according to my taste"), who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, and functional analysis. Hausdorff was Jewish, and life became difficult for him and his family after the '' Kristallnacht'' of 1938. The next year he initiated efforts to emigrate to the United States, but was unable to make arrangements to receive a research fellowship. On 26 January 1942, Hausdorff, along with his wife and his sister-in-law, died by suicide by taking an overdose of veronal, rather than comply with German orders to move to the Endenich camp, and there suffer the likely implications, about which he held no illusions. Life Childhood and youth Hausdorff's father, the Jewish merchant Louis Hausdorff (1843–1896), moved with his young family to Leipzig in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximal Element
In mathematics, especially in order theory, a maximal element of a subset S of some preordered set is an element of S that is not smaller than any other element in S. A minimal element of a subset S of some preordered set is defined dually as an element of S that is not greater than any other element in S. The notions of maximal and minimal elements are weaker than those of greatest element and least element which are also known, respectively, as maximum and minimum. The maximum of a subset S of a preordered set is an element of S which is greater than or equal to any other element of S, and the minimum of S is again defined dually. In the particular case of a partially ordered set, while there can be at most one maximum and at most one minimum there may be multiple maximal or minimal elements. Specializing further to totally ordered sets, the notions of maximal element and maximum coincide, and the notions of minimal element and minimum coincide. As an example, in the collecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. When quantified, A \subseteq B is represented as \forall x \left(x \in A \Rightarrow x \in B\right). One can prove the statement A \subseteq B by applying a proof technique known as the element argument:Let sets ''A'' and ''B'' be given. To prove that A \subseteq B, # suppose that ''a'' is a particular but arbitrarily chosen element of A # show that ''a'' is an element of ''B''. The validity of this technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |