|
Nesbitt's Inequality
In mathematics, Nesbitt's inequality, named after Alfred Nesbitt, states that for positive real numbers ''a'', ''b'' and ''c'', :\frac + \frac + \frac \geq \frac, with equality only when a=b=c (i. e. in an equilateral triangle). There is no corresponding upper bound as any of the 3 fractions in the inequality can be made arbitrarily large. It is the three-variable case of the rather more difficult Shapiro inequality, and was published at least 50 years earlier. Proof First proof: AM-HM inequality By the AM- HM inequality on (a+b),(b+c),(c+a), :\frac \geq \frac. Clearing denominators yields :((a+b)+(a+c)+(b+c))\left(\frac + \frac + \frac\right)\geq 9, from which we obtain :2\frac + 2\frac + 2\frac \geq 9 by expanding the product and collecting like denominators. This then simplifies directly to the final result. Second proof: Rearrangement Supposing a \ge b \ge c, we have that :\frac \ge \frac \ge \frac. Define :\vec = (a,b,c)\quad and \quad\vec = \left(\frac , \frac , \frac\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
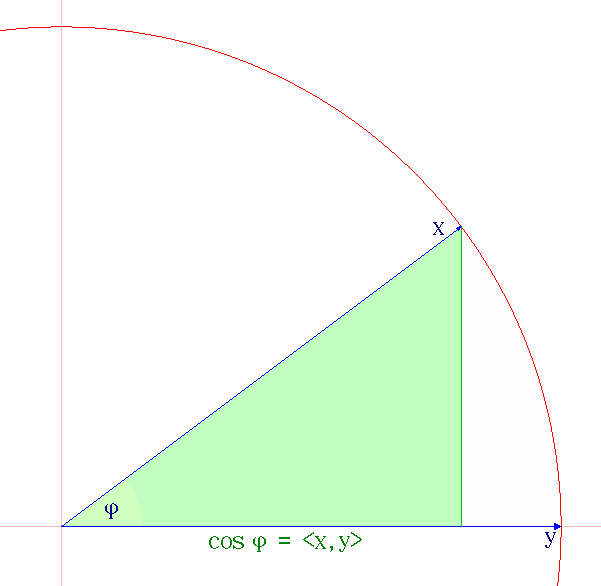
AM-HM
In mathematics, the three classical Pythagorean means are the arithmetic mean (AM), the geometric mean (GM), and the harmonic mean (HM). These means were studied with proportions by Pythagoreans and later generations of Greek mathematicians because of their importance in geometry and music. Definition The three Pythagorean means are defined by the equations \begin \operatorname \left( x_1,\; \ldots,\; x_n \right) &= \frac, \\ pt \operatorname \left( x_1,\; \ldots,\; x_n \right) &= \sqrt \text \\ pt \operatorname \left( x_1,\; \ldots,\; x_n \right) &= \frac . \end Properties Each mean, \operatorname, has the following properties for positive real inputs: ; First-order homogeneity: \operatorname(bx_1, \ldots, bx_n) = b \operatorname(x_1, \ldots, x_n) ; Invariance under exchange: \operatorname(\ldots, x_i, \ldots, x_j, \ldots) = \operatorname(\ldots, x_j, \ldots, x_i, \ldots) for any i and j. ; Monotonicity: if a \leq b then \operatorname(a,x_1,x_2,\ldots x_n) \leq \operato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petar Vasić
Petar (, sr-Cyrl, Петар) is a South Slavic masculine given name, their variant of the Biblical name Petros cognate to Peter. Derivative forms include Pero, Pejo, Pera, Perica, Petrica, Periša. Feminine equivalent is Petra. People mononymously known as Petar include: * * * Petar of Serbia ( – 917), early Prince of the Serbs * Petar of Duklja (), early archont in Dioclea * Petar Krešimir (died 1074/1075), King of Croatia and Dalmatia * Petar Delyan (r. 1040-1041), Bulgarian rebel, declared Emperor of Bulgaria Notable people with the name are numerous: * See also * Sveti Petar (other) * Petrov (other) * Petrić * Petričević Petričević ( sr-Cyrl, Петричевић) is a Serbo-Croatian surname, a patronymic A patronymic, or patronym, is a component of a personal name based on the given name of one's father, grandfather (more specifically an avonymic), or an ea ... References {{reflist Bulgarian masculine given names Croatian mascu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dragoslav Mitrinović
Dragoslav S. Mitrinović (Serbian Cyrillic: Драгослав Митриновић; 23 June 1908 – 2 April 1995) was a Serbian mathematician known for his work in differential equations, functional equations, complex analysis. He authored near 300 scientific journal papers and more than twelve books in his area. Biography Born in Smederevo, he studied in Pristina and Vranje, graduating in mathematics at the University of Belgrade Faculty of Philosophy (1932). He earned a Ph.D. (1933) on a study of differential equations entitled ''Istraživanja o jednoj važnoj diferencijalnoj jednačini prvog reda'' (that is, ''Investigations of an important differential equation of the first order''), advised by Mihailo Petrović. He then worked as a secondary school teacher until 1946, when he visited University of Paris (1946) before joining the faculty at Skopje University in Macedonia where he founded the school of mathematics and two journals, eventually being elected to the Maced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jensen's Inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation (or equivalently, the opposite inequality for concave transformations). Jensen's inequality generalizes the statement that the secant line of a convex function lies ''above'' the graph of the function, which is Jensen's inequality for two points: the secant line consists of weighted means of the convex function (for ''t'' ∈ ,1, :t f(x_1) + (1-t) f(x_2), while the g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is convex if its epigraph (mathematics), ''epigraph'' (the set of points on or above the graph of the function) is a convex set. In simple terms, a convex function graph is shaped like a cup \cup (or a straight line like a linear function), while a concave function's graph is shaped like a cap \cap. A twice-differentiable function, differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain of a function, domain. Well-known examples of convex functions of a single variable include a linear function f(x) = cx (where c is a real number), a quadratic function cx^2 (c as a nonnegative real number) and an exponential function ce^x (c as a nonnegative real number). Convex functions pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemma (mathematics)
In mathematics and other fields, a lemma (: lemmas or lemmata) is a generally minor, proven Theorem#Terminology, proposition which is used to prove a larger statement. For that reason, it is also known as a "helping theorem" or an "auxiliary theorem". In many cases, a lemma derives its importance from the theorem it aims to mathematical proof, prove; however, a lemma can also turn out to be more important than originally thought. Etymology From the Ancient Greek λῆμμα, (perfect passive εἴλημμαι) something received or taken. Thus something taken for granted in an argument. Comparison with theorem There is no formal distinction between a lemma and a theorem, only one of intention (see Theorem#Terminology, Theorem terminology). However, a lemma can be considered a minor result whose sole purpose is to help prove a more substantial theorem – a step in the direction of proof. Well-known lemmas Some powerful results in mathematics are known as lemmas, first named for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Titu's Lemma
In mathematics, the following inequality is known as Titu's lemma, Bergström's inequality, Engel's form or Sedrakyan's inequality, respectively, referring to the article ''About the applications of one useful inequality'' of Nairi Sedrakyan published in 1997, to the book ''Problem-solving strategies'' of Arthur Engel published in 1998 and to the book ''Mathematical Olympiad Treasures'' of Titu Andreescu published in 2003. It is a direct consequence of Cauchy–Bunyakovsky–Schwarz inequality. Nevertheless, in his article (1997) Sedrakyan has noticed that written in this form this inequality can be used as a proof technique and it has very useful new applications. In the book ''Algebraic Inequalities'' (Sedrakyan) several generalizations of this inequality are provided. Statement of the inequality For any real numbers a_1, a_2, a_3, \ldots, a_n and positive reals b_1, b_2, b_3,\ldots, b_n, we have \frac + \frac + \cdots + \frac \geq \frac. ( Nairi Sedrakyan (1997), Arthu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean-geometric Mean Inequality
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms. Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include both rational and irrational numbers. Another distinction is based on the numeral system employed to perform calculations. Decimal arithmetic is the most common. It uses the basic numerals from 0 to 9 and their combinations to express numbers. Binary arithmetic, by contrast, is used by most computers and represents numbers as combinations of the basic numerals 0 and 1. Computer arithmetic deals with the specificities of the implemen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alfred Mortimer Nesbitt
Alfred may refer to: Arts and entertainment *''Alfred J. Kwak'', Dutch-German-Japanese anime television series * ''Alfred'' (Arne opera), a 1740 masque by Thomas Arne * ''Alfred'' (Dvořák), an 1870 opera by Antonín Dvořák *"Alfred (Interlude)" and "Alfred (Outro)", songs by Eminem from the 2020 album ''Music to Be Murdered By'' Business and organisations * Alfred, a radio station in Shaftesbury, England *Alfred Music, an American music publisher *Alfred University, New York, U.S. *The Alfred Hospital, a hospital in Melbourne, Australia People * Alfred (name) includes a list of people and fictional characters called Alfred * Alfred the Great (848/49 – 899), or Alfred I, a king of the West Saxons and of the Anglo-Saxons Places Antarctica * Mount Alfred (Antarctica) Australia * Alfredtown, New South Wales * County of Alfred, South Australia Canada * Alfred and Plantagenet, Ontario ** Alfred, Ontario, a community in Alfred and Plantagenet * Alfred Island, Nunavut * Moun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |